如何实现SPWM控制技术

图2-19是SPWM变频器的原理框图。这种采用二极管组成不可控整流器及由自关断器件组成逆变器的主电路方案，是目前应用最多的一种方案。图中逆变器的主开关器件是BJT，从原理上说，当然也可以采用GTO或IGBT。

逆变器开关模式信号，通常情况下利用三相对称的正弦波参考信号与一个共用的三角波载频信号互相比较来生成，如图2-19b所示。

控制上常有单极性和双极性两种情况：

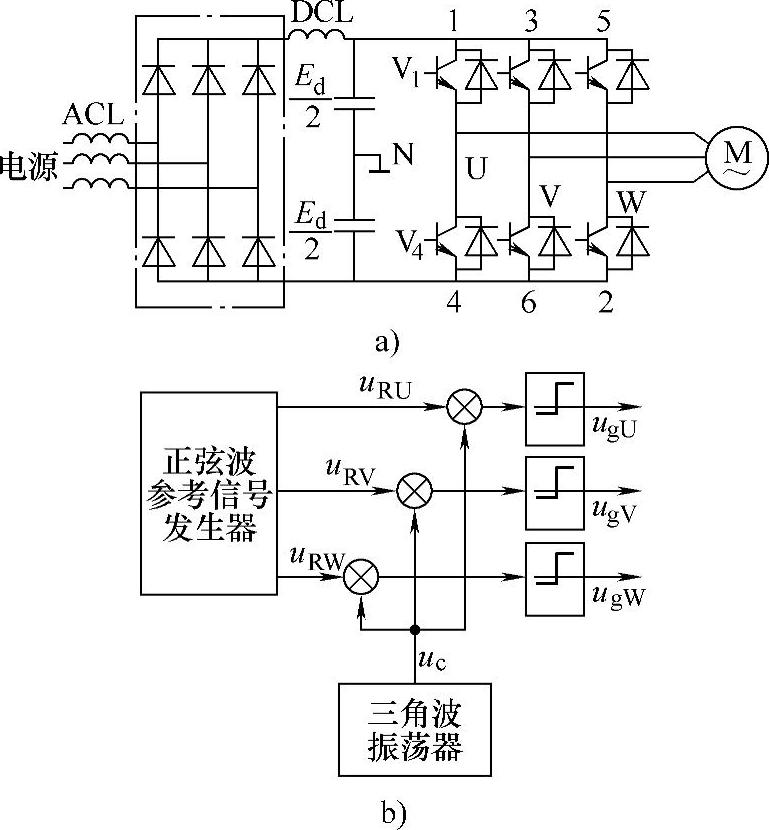
图2-19 SPWM变频器

a）主电路 b）控制电路框图

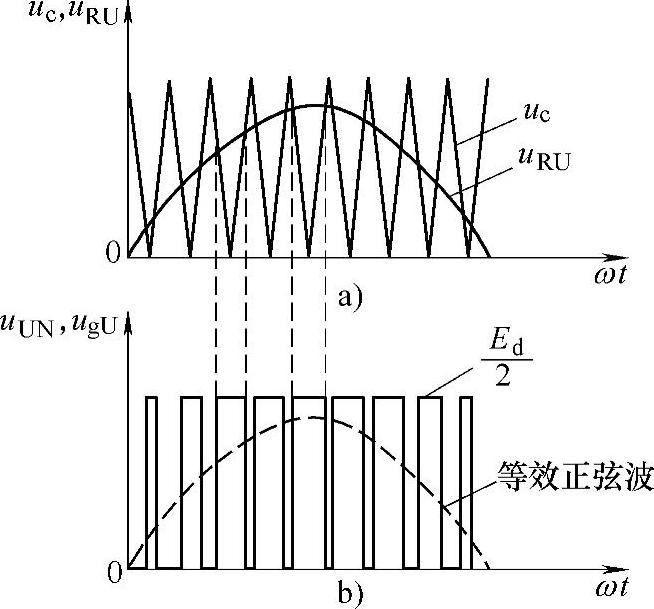
所谓单极性控制是指在输出的半个周波内同一相的两个导电臂仅一个反复通断而另一个始终截止。例如U相的正半周波，图2-19a中的V₁反复通断，而V₄始终截止。单极性控制情况下，图2-19b中的u_RU、u_c及u_gU的波形如图2-20a所示。当u_RU高于u_c时，u_gU为“正”电平；当u_RU低于u_c时，u_gU为“零”电平。由于载频信号u_c等腰三角波的两腰是线性变化的，它与光滑的正弦参考信号u_RU相比较，得到的各脉冲的宽度也随时间按正弦规律变化，形成了SPWM的控制波形u_gU。u_gU作为主电路中V₁的基极控制信号，控制V₁的反复通断。所以在正半周波内，图2-19a中的U相输出电位波形u_UN与u_gU是相似的。相对于直流中点而言，u_UN的幅度是E_d/2，并且保持恒定，如图2-20b所示。以上分析的是正半周波的情况，负半周波与此类似。

所谓双极性调制是指在输出的半个周波内同一相的两个导电臂互补交替通断，例如U相的正半周波：

这样即可得到双极性的U点电位U_UN，如图2-21b所示。各脉冲的幅值+E_d/2和-E_d/2是以直流中点N为参考点得到的。

由图2-20及图2-21的波形图可以想象到：改变参考信号波u_R的频率，输出频率会随之改变；改变u_R的幅值，则输出电压的幅值亦会随之改变。如果控制u_R，使其频率、幅值协调变化，则可以按图2-4所示的关系对变频器进行U/f控制。这是变频器的PWM方式的最基本的概念。

(www.xing528.com)

图2-20 单极性脉宽调制方法与波形

a）正弦参考波与三角载波 b）输出SPWM波形

通常情况下，单极性SPWM多采用单极性的载频三角波，双极性SPWM则采用双极性的载频三角波。从控制方法上看，采用单极性的载频三角波完全可以实现双极性控制，或者反过来采用双极性载频三角波也完全可以实现单极性控制。但如果这样，在其他条件相同的情况下，输出电压的谐波含量将有所增加^[4]。

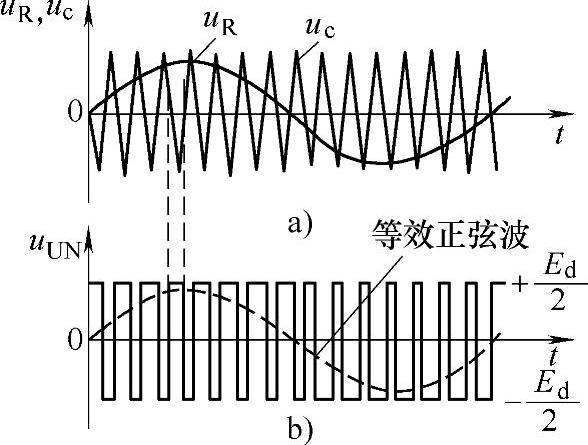
图2-21 双极性调制

图2-22a的三相SPWM变频器，其逆变器的控制采用双极性调制时，三相SPWM逆变器的波形图如图2-22b所示。图中线电压只画出了u_AB，相电压只画出了U_AO。

对图2-22说明如下。图中的波形是三相PWM控制形成的。载频三角波三相公用，而参考电压波是三相对称正弦波，为u_ra、u_rb和u_rc，波形u′_AO、u′_BO和u′_CO是A、B、C三个相端点的电位（以直流中点O′为参考点），并非电机电压的物理波形，而U_AB、U_AO分别为电机的线电压和相电压，它们才是物理波形。

线电压和相电压的波形是很容易由观察法得到的，例如在图2-22b中的ΔT时段内，由三角波和三相正弦参考波比较，可得ΔT时间内主电路中的5、6和1臂导通。如图2-22a中右图所示，该图表示5、6、1导通，因此可以判断U_AB=+U_d，U_BC=-U_d，而U_CA=0；还可以利用三相对称负载的分压关系判断U_AO=+U_d/3、U_BO=-2U_d/3，而U_CO=+U_d/3。在图2-22b的ΔT时间内，U_AB、U_AO瞬时值，可以在对应波形图上验证。

图2-22 双极性调制的三相SPWM变频器的输出波形

图中还出现若干个时间段，1、3、5或者4、6、2同时导通，电机处于短路耗能状态，旋转磁场停转。在后文的SVPWM节中，这种情况下的电压空间矢量被称为零矢量。