【摘要】：如图7-19所示的环形壳体，壳体的半径为r，环壳中心线的半径为R，壁厚为S。当环形壳体受内压力p作用后，产生环向应力σ1和经向应力σ2。经向应力σ1可用区域平衡方程式求解，现取两个母线分别为om、on的同轴旋转锥面截割壳体，如图7-19所示。图7-19 环形壳体的应力内力与介质压力的轴向平衡条件为Sσ12πρsinθ=pπ整理上式得由于ρ=R+rsinθ，则由式可知，环向应力σ1与有关，也与θ角有关。
如图7-19所示的环形壳体，壳体的半径为r，环壳中心线的半径为R，壁厚为S。当环形壳体受内压力p作用后，产生环向应力σ1和经向应力σ2（均为膜应力）。由于环形壳体是回转壳体，所以可以用薄膜理论求解其应力。
经向应力σ1可用区域平衡方程式求解，现取两个母线分别为om、on的同轴旋转锥面截割壳体，如图7-19所示。
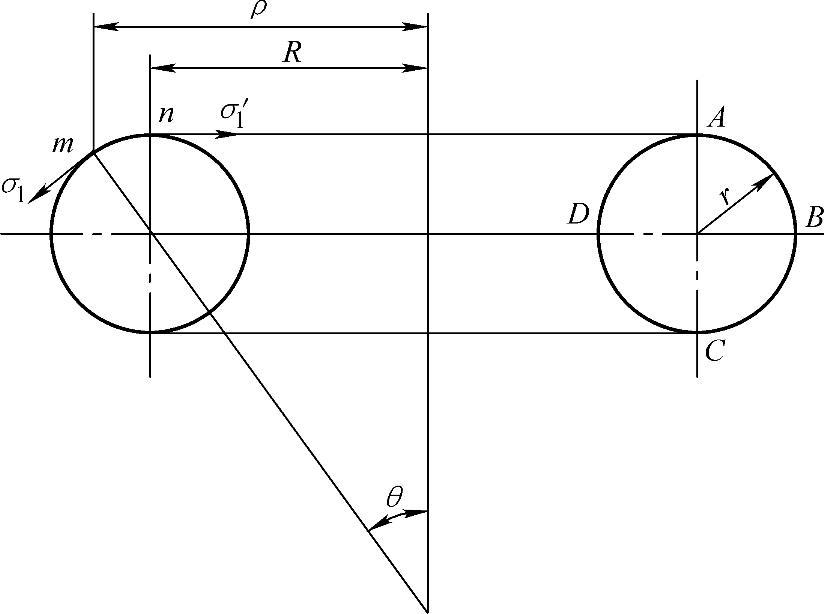
图7-19 环形壳体的应力
内力与介质压力的轴向平衡条件为
Sσ12πρsinθ=pπ（ρ2-R2）
整理上式得
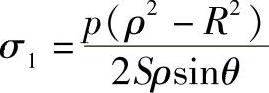
由于ρ=R+rsinθ，则
由式（7-58）可知，环向应力σ1与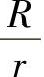
有关，也与θ角有关。
经向应力σ2可由微体平衡方程式确定，即
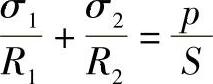
或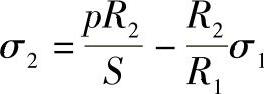
m点的第一曲率半径和第二曲率半径分别为
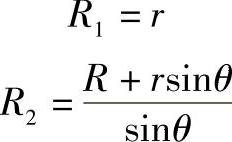(www.xing528.com)
将R1、R2代入上式得
从式（7-59）可知，经向应力σ2与θ角及R均无关，而且它恒小于σ1，即危险应力是σ1。再分析式（7-58），以确定其最大应力的数值及位置，现取
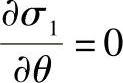
得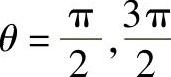
显然极值在B点和D点，下面确定4个特殊点的应力，即
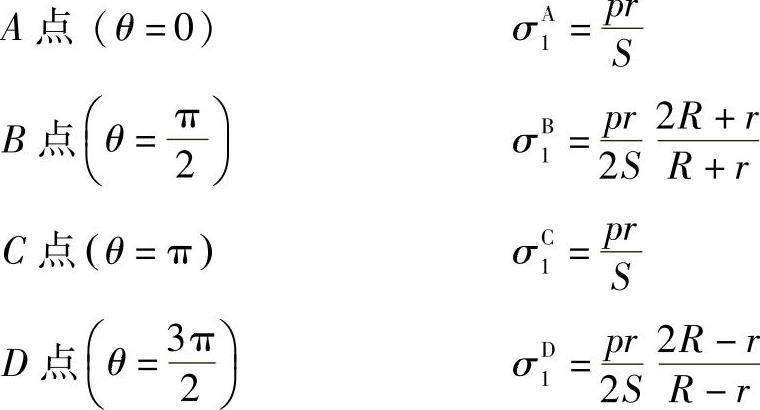
这里D点的应力最大。若用壳体的直径d代替半径r，则壁厚的计算公式为
式中 p——设计压力（N/m2）；
d——环形壳体直径（m）；
R——环形壳体的弯曲半径（m）；
[σ]t——材料的许用应力，按压力容器设计规定选取（N/m2）；
C——壁厚附加量（m）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
