具有内加强筋板的长圆形柱壳设计方案优化

在长圆形柱壳的中央采用与壳体同种材料的厚度为S的平板作为内加强筋板，如图7-18a所示。由于截面B对称于x轴，所以横剪力与转角均为零，而截面A的y向挠度受筋板约束。这里仍按前面介绍的力学模型，即将单位长度柱壳的四分之一作为悬臂曲梁。由图7-18b可知，曲梁有如下内力：N_a、N_b是法向力，以拉为正；M_a、M_b是弯矩，使内壁受拉为正；Q_a是剪力，使截面反时针转为正。自由端的已知变形为转角，θ=0；y向挠度为筋板拉伸变形，。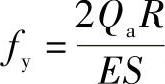

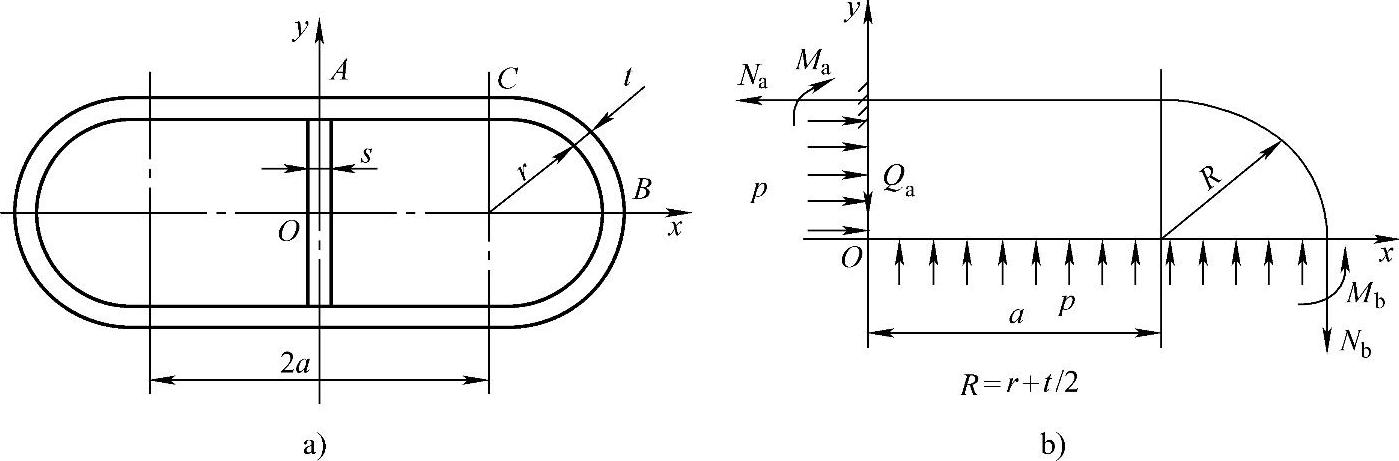
图7-18 带加强筋的长圆形壳

1.静力平衡条件

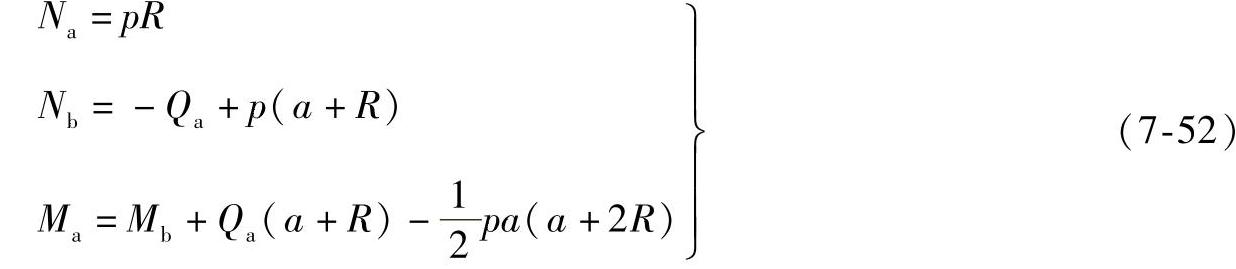
2.补充方程

3个平衡方程中有5个未知量，所以应按已知的位移用单位截面载荷法作两条补充方程。根据截面B的转角为零，可得

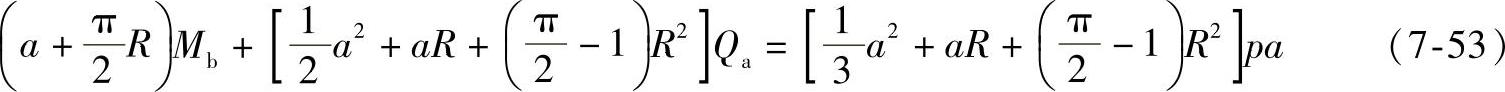
由截面B的y向位移可得

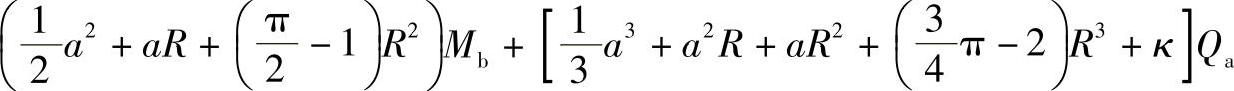
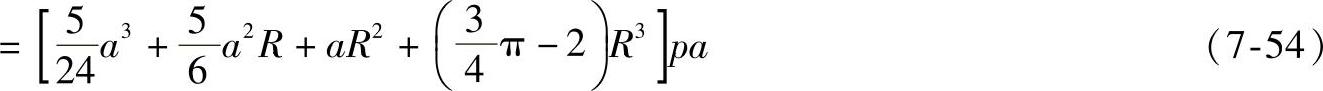
其中

式中 t——柱壳的厚度（m）；

S——筋板的厚度（m）；

R——筋板的半长（图7-17）（m）；

μ——泊松比。

联解式（7-53）、式（7-54），可求得M_b及Q_a，利用式（7-52），可解长圆形柱壳危险截面的全部内力，利用式（7-43），可作强度检验。

下面求解M_b及Q_a。式（7-53）、式（7-54）可以写成如下形式：

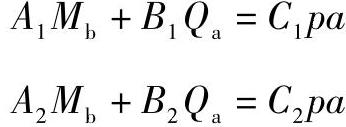
联解上两式可得

(www.xing528.com)

其中

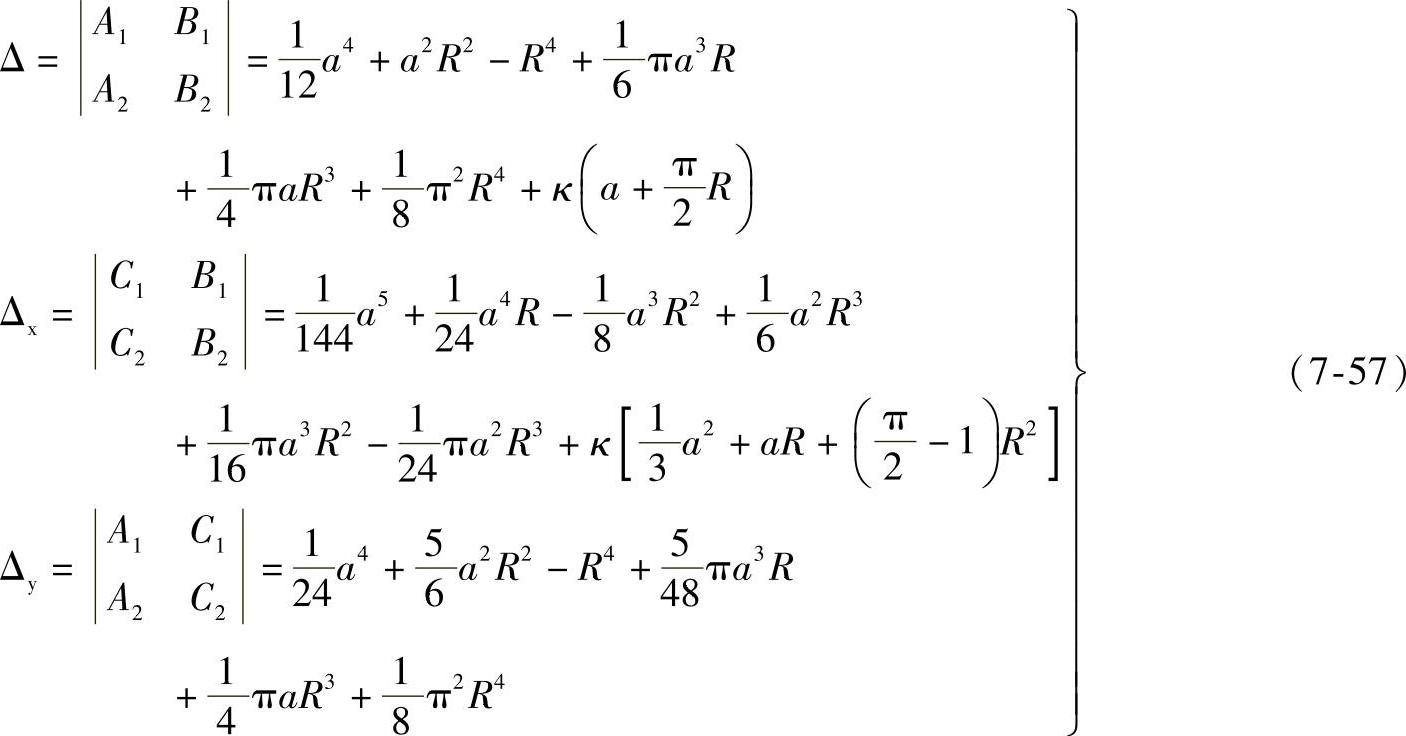
例7 长圆形柱壳的a=900mm，R=600mm，p=0.1MPa，t≤200℃，材料为Q345，板厚（扣除附加量）t=38mm，查200℃时Q345的许用应力[σ]^t=150MPa。

解：（1）无加强壳体

为了与有加强筋板的壳体作比较，先按无加强壳体作计算

r_min=R=0.6m

r_max=a+R=1.5m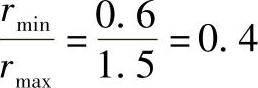，由表7-2查得f=1.0681，回转半径为

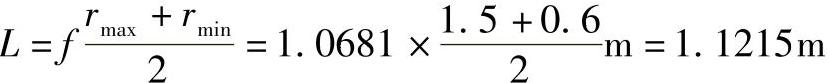
由式（7-42）得

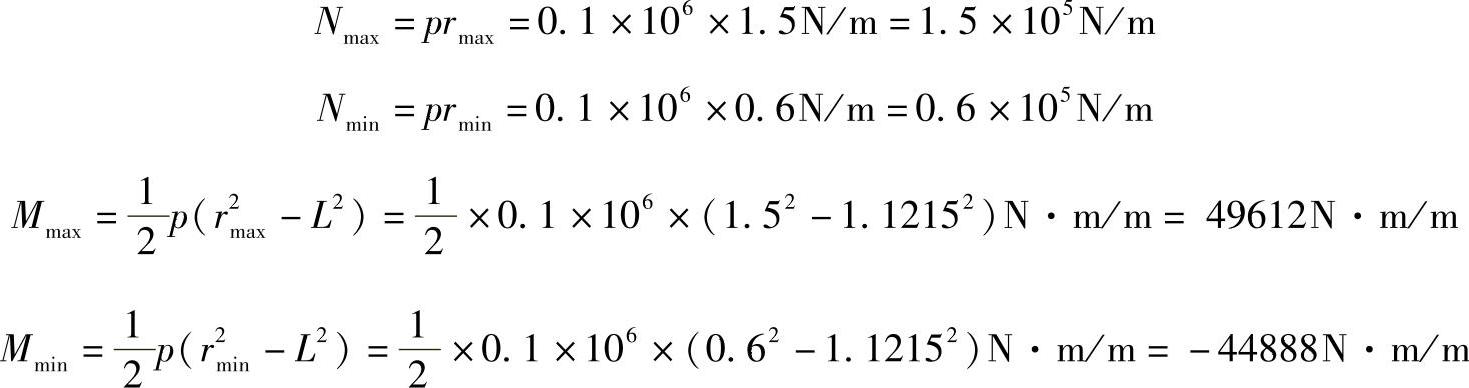
最大应力在截面B的内侧

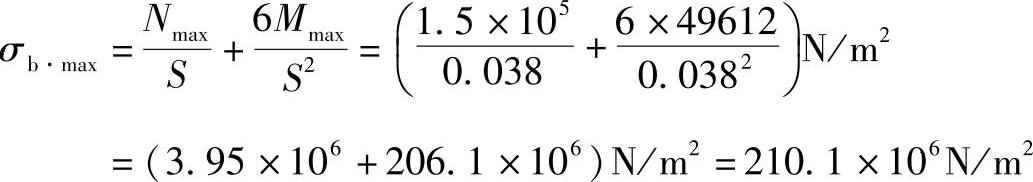
根据非圆形截面壳体的允许应力[σ_m]=1.5[σ]^t=1.5×150=225MPa，本设备可以使用，从计算结果看弯曲应力比膜应力大得多。

（2）有加强筋的壳体

为了比较加强筋的作用，现取3种筋板：“1”绝对刚性（相当于壁厚S为无穷大）；“2”厚度同壳体，即38mm；“3”S=1mm。

先按式（7-57）计算Δ、Δ_x、Δ_y，再按式（7-56）和式（7-52）计算M_b、Q_a、N_a、N_b及M_a，这里κ值使用式（7-55）计算。计算结果如下：

从计算结果看危险截面为A截面，而且由无加强时的负值变成正值，从数值上看最大弯矩M_a比无加强壳体的最大弯矩M_b值要小。分析本例的3种筋板，第一种无限厚是理想状态，第3种厚1mm在工程中无法使用。这3种筋板的计算结果相差无几，工程中常用的是筋板的厚度与壳体相等，它与筋板为绝对刚性的计算结果几乎一样，所以筋板厚度的变化对计算结果不起太大作用，可以用绝对刚性的计算公式，即令κ=0进行计算更为方便。

由于危险截面的弯矩下降，这里假定壳体厚度为24mm，危险应力在A截面内侧。

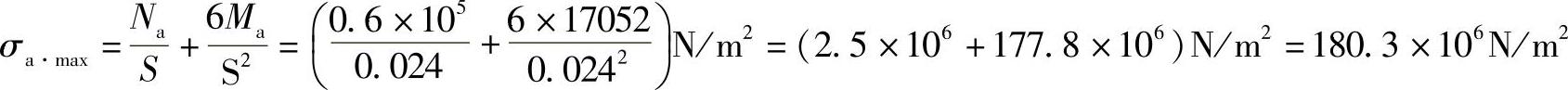
从计算可知，采用加强筋板加强是有效的。非圆形截面壳体采用内加强的效果比外加强好。