曲梁弯曲时的弯曲应力分析

设一几何尺寸及外载荷均对称于xcz平面的曲梁（图7-11），在弯矩M的作用下微元面积dF上的应力为σ，内力为σdF。由于曲梁有对称平面，所以可以用对称平面代表曲梁。这里用材料力学中的研究直梁的方法来分析曲梁。根据平面变形假设，即变形前垂直于x轴的平面，受力变形后仍旧是垂直于x轴的平面。x轴是中性轴。图7-12所示是对称平面xcz中的dϕ一段，O_1-O₂是形心轴线，C₁-C₂是中性轴。当曲梁受弯矩M作用时，截面2-2绕y轴（即C₂点）旋转δdϕ角，旋转后仍是平面。现在研究其中一条纤维A₁A₂，由于截面2的转动，该纤维伸长了A₂D₂，其相对伸长为

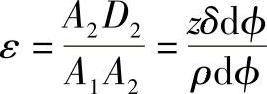
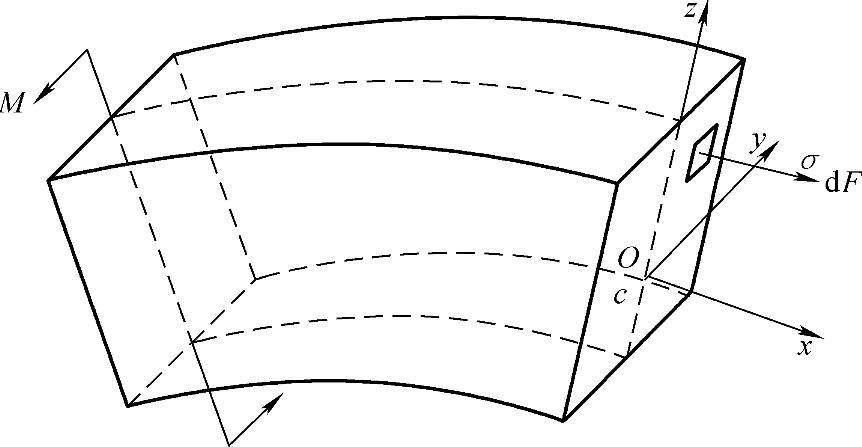
图7-11 受纯弯曲的曲梁

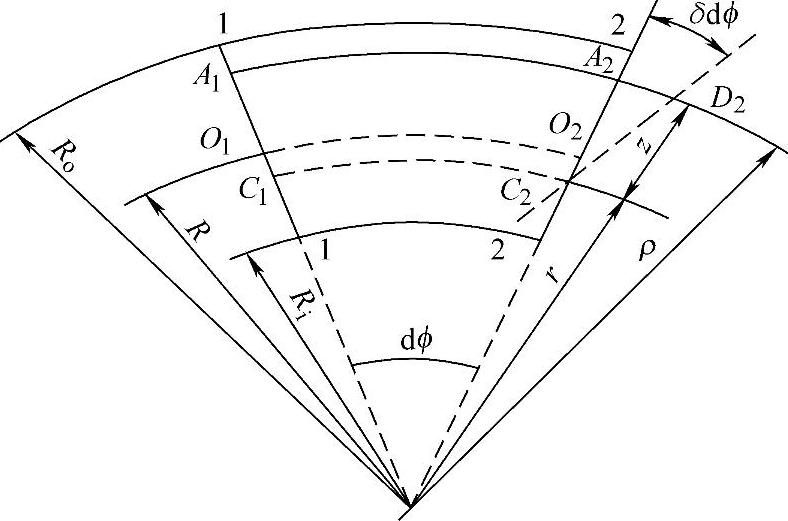
图7-12 受纯弯曲梁的变形关系

根据胡克定律：

图7-11所示曲梁的两个力平衡条件为

首先将式（7-44a）代入式（7-44b），即

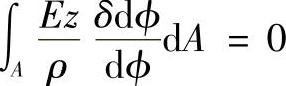
由于E、

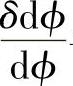
与微元面积dA的位置无关，且都不等于零，所以

由于z=ρ-r，所以

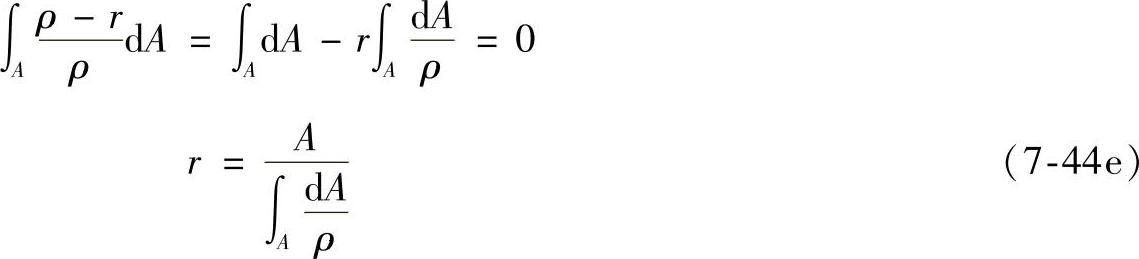(www.xing528.com)

式（7-44e）可用来计算中性层的位置。

再将式（7-44a）代入式（7-44c），即

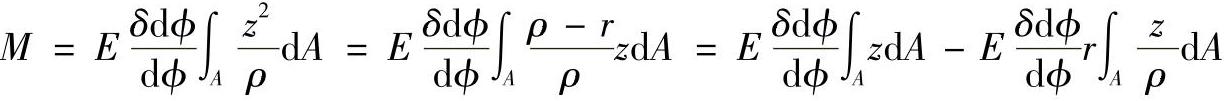
由式（7-44d）可知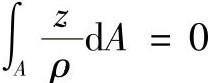

所以

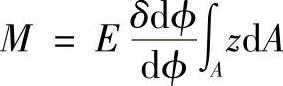
令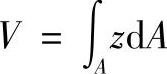

这里V是静矩，又称为面积矩，于是

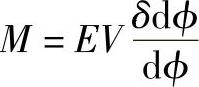
或

将式（7-44f）代入式（7-44a），可得

曲梁弯曲应力的分布规律如图7-13所示。由图可知，中性轴C—C与形心轴O—O不重合，应力的分布也不像直梁那样按直线分布。由图可知内侧应力的数值比按直线分布规律的值要大得多。

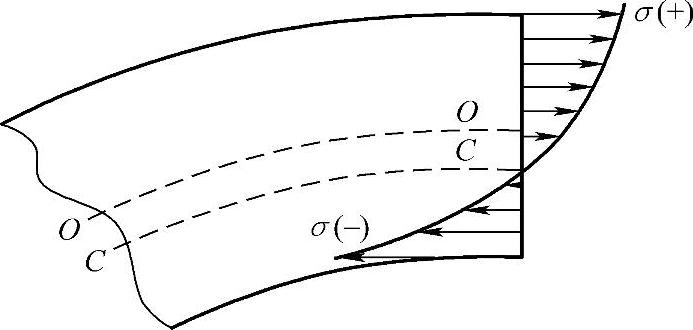
图7-13 曲梁的应力分布