计算公式及其应用详解

前面分析了四种非圆形截面的壳体，若用半径的算术平均值代替回转半径，其误差不大。推广认为所有的非圆形截面壳体均可用最大流动半径及最小流动半径的算术平均值代替回转半径的积分式，即。

当回转半径L确定后，即可计算壳体最大弯矩和最小弯矩，以及任意点C的弯矩：

1.危险截面的确定

如果近似计算，即回转半径L直接取最大、最小流动半径的算数平均值，则危险截面在最大流动半径处。证明如下：

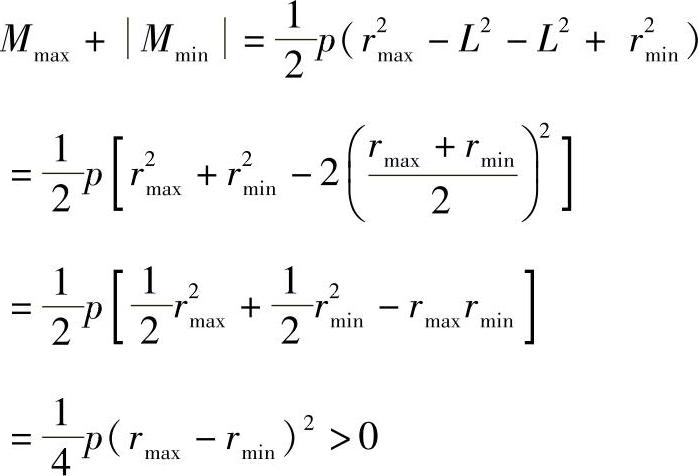
如果精确计算，即回转半径式中引入壳体形状系数f，则危险截面不是在r_max处，便是在r_min处，即这两个截面必须同时检验。

2.计算公式

（1）回转半径

式中 L——回转半径（m）；

r_max、rmin——分别为非圆形截面壳体的最大流动半径和最小流动半径（中径）（m），可以在图纸上直接量得；

f———非圆形截面壳体的形状系数，由表7-2、表7-3查取。对于其他形状的壳体，可取f=1，这时L是近似值，仅能作近似计算。

内力：

当需要计算任意截面C的弯矩时，则

式中 N_max、N_min——分别为r_max与r_min处单位长度的法向力（N/m）；

M_max、Mmin——分别为r_max与rmin处单位长度的弯矩（N·m/m）；

p——壳体内介质压力（N/m²）；

r_C——壳体上任意点C的流动半径（壳体中心O到C点距离）（m）。

（2）应力

由于非圆形截面壳体中的弯曲应力是主要的，所以两个危险截面的应力必须同时检验，如果仅作近似计算，则只需检验最大流动半径处的应力。

最大流动半径处内壁应力：

最小流动半径处外壁应力：

式中 S——壳体厚度（扣除材料壁厚附加量）（m）；

[σ_m]——壳体的允许应力（N/m²）。由于σ₁、σ₂中的主要部分是弯曲应力，所以取[σ_m]=1.5[σ]^t。这里[σ]^t可按压力容器的

设计规定取值。

例4 试用例1的数据按近似方法计算椭圆形截面壳体截面A及截面B的弯矩。

解：已知r_max=a=500mm，r_min=b=250mm，p=0.25MPa

回转半径为(www.xing528.com)

B截面的弯矩为最大弯矩：

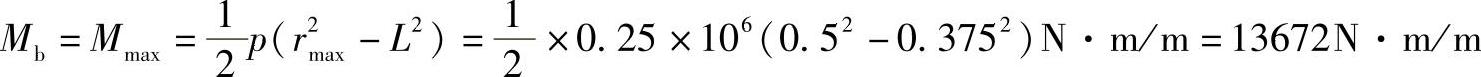
A截面的弯矩为最小弯矩：

例1的精确解：M_b=13318N·m/m，M_a=-9651N·m/m

最大弯矩的误差：

误差很小，如果用形状系数f₁修正回转半径，即得精确解。

例5 试用例3的数据计算带圆角的矩形壳体的最大弯矩和最小弯矩。

解：已知p=0.25MPa，a=400mm，b=280mm，r=100mm

（1）近似计算

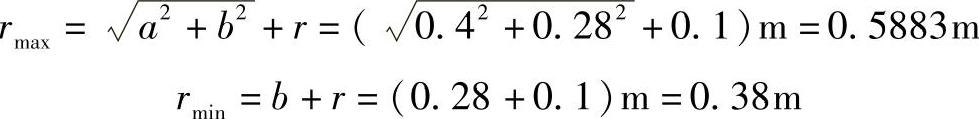
回转半径为

最大弯矩在处

最小弯矩为

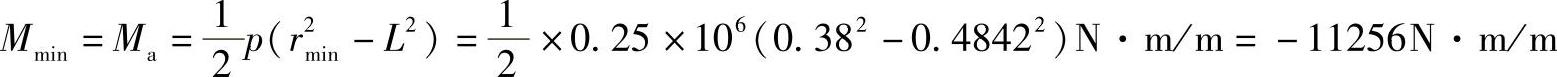
例3的精确解为

M_max=12043N·m/m，M_min=-13164N·m/m

最大弯矩的计算误差：

最小弯矩的计算误差：

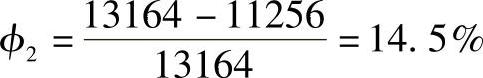
精确解的M_min和近似解的M_max的计算误差：

误差不太大，工程中可以应用。结果偏于保守。

（2）精确解将形状系数引入回转半径中，由，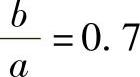

查表7-3得f₄=1.032

与例3的精确解一样。

从本例的计算可知，如果有壳体的形状系数，则可直接求精确的回转半径，弯矩及应力。但如果无法确定形状系数，则近似计算，弯矩和应力便有一定误差，但误差不大，而且偏于保守，工程中是允许的。