如何计算壳体的回转半径？

回转半径相当于壳体的平均半径，若可用最大半径和最小半径的算术平均值代替回转半径，则弯矩计算非常方便。下面对几种已算出M_b的典型壳体作分析。

1.椭圆形壳体的回转半径

椭圆形壳体B截面的弯矩可用式（7-11）计算，即

上式与式（7-36）比较，显然

式中 E（k）、G（k）——椭圆形壳体的计算系数，可由表7-1查得。

由于L相当于平均半径，若取最大半径与最小半径的算术平均值，则会有一定的误差，现在来计算这误差有多少。令

式中 a、b——分别为椭圆形壳体的长轴半径和短轴半径；

L₁——椭圆形壳体的回转半径；

f₁——椭圆形壳体的形状系数。

f₁可由下式直接计算：

f₁的计算结果见表7-2。由表7-2可知，当时，f<1.0340。所以如果椭圆形壳体的时，完全可以用长短轴半径的算术平均值代替回转半径，即取

如果进行了这样的简化，则椭圆形壳体的弯矩计算公式非常简单，作为强度计算使用时不会产生很大的误差。即使在极限的情况下，即在时，L₁的计算误差也仅15%。本章已算出M_b的几种特定壳体，如椭圆形壳体，则可在算术平均值的基础上乘上表7-2的f值，即利用公式（7-39）进行精确计算。

表7-2 几种壳的形状系数f

2.其他壳体的回转半径

（1）近似椭圆形壳体

比较近似椭圆形壳体截面B的弯矩式（7-28）与式（7-36）

(www.xing528.com)

同样回转半径与算术平均值之间也存在如下关系：

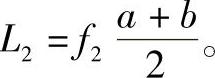
这里f₂是近似椭圆壳体的形状系数，由表7-2查得。从表中数值可知，f₂≈f₁，说明这两种壳体的受力状态几乎相同。

（2）长圆形壳体

由图7-8和图7-10可知，符号a、b的定义不同，为了使用回转半径的概念，令图7-10中的a、b带有“′”，即

a′=a+rb′=b+r

这样由式（7-31）的第3式与式（7-36）相等，得

解得

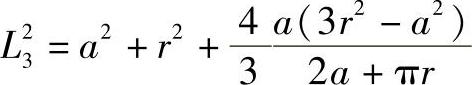
将L₃值代入式（7-39），可得长圆形壳体的形状系数

长圆形壳体的形状系数也列在表7-2中，从表中数值可知，f₃的数值也在1附近。

（3）带圆角的矩形壳体带圆角的矩形壳体的长轴半径为a+r，短轴半径为b+r，最大流动半径为，最小流动半径为b+r，其算术平均值为

利用式（7-23h）及式（7-36）解得回转半径为

于是这一壳体的形状系数为

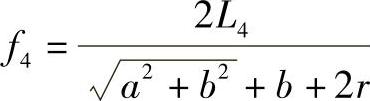
计算结果列入表7-3。由表7-3可知，f₄也在1附近，其中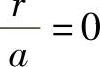的壳体即是无圆角的矩形壳体。

表7-3 带圆角的矩形壳体的形状系数f4