受力分析：非圆形截面壳体的Mb计算与回转半径求解方法

图7-10a所示承受内压力p的非圆形截面壳体，其截面形状是随意的，同样，它有两个对称轴x，y。壳体的长轴半径为a，短轴半径为b。由于截面对称于x轴和y轴，所以只需研究其1/4即ACB段即可。正如前面所述，可以将1/4的壳体段简化成以A为固定端，B为自由端的悬臂曲梁。在对称轴上的截面A和截面B的横剪力和转角均为零。根据曲梁ACB的静力平衡条件（图7-10b），可求得和前面一样的3个平衡方程。

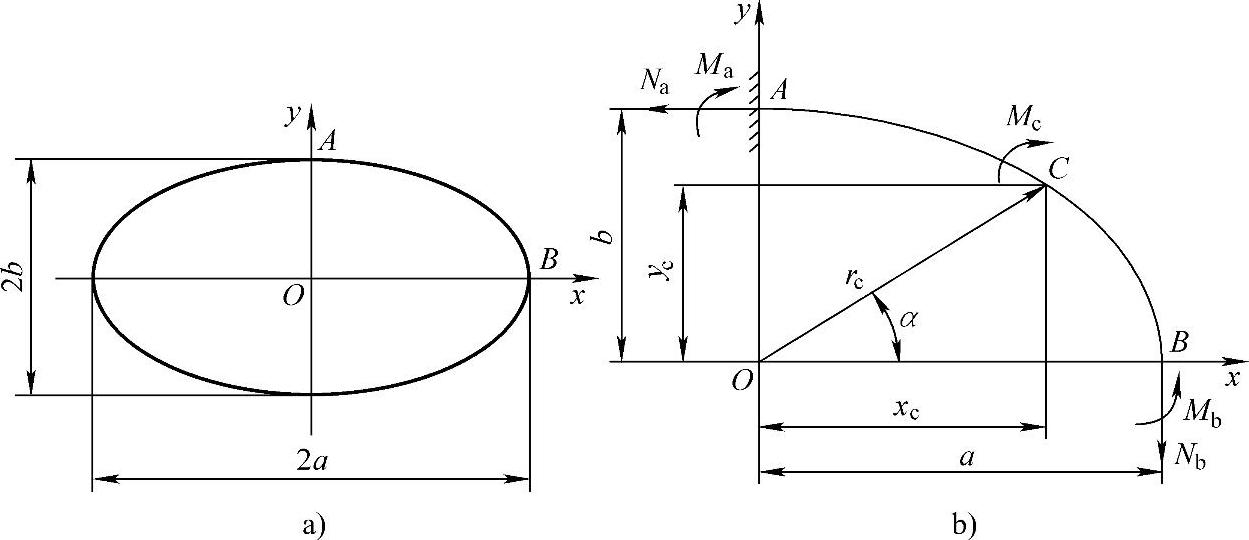
图7-10 一般非圆形截面壳体及其受力简图

在运用单位载荷法列补充方程时，需要曲梁上任意截面C的弯矩M_c，这可以由CB段的力平衡条件求得，即

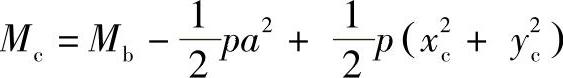
由于x²_c+y²_c=r²_c，则

式中 r_c——任意点C到壳体中心O的距离，或称为壳体的流动半径，由图7-10b可知，它随角α而变。

当壳体的形状确定，则r_c与α的关系是确定的，在图示的情况下，当α=0时，r_c=a，此时M_c=M_b；当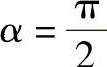时，r_c=b，此时M_c=M_a。

根据截面B的转角公式（7-9）得

式中 M_L——在截面B上作用单位力矩M₀=1时，曲梁任意截面C上的弯矩。

显然

M_L=1

将上式与式（7-34）代入式（7-9）得(www.xing528.com)

对已知壳体而言，p、M_b、a均与dl的位置无关，而r_c随C的位置而变，即随dl的位置而变，于是

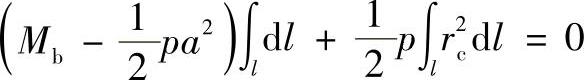
或

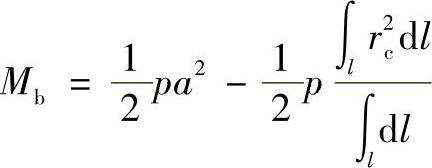
令

则

式中 L——壳体的回转半径，相当于壳体的平均半径。

对于一定的壳体，r_c、dl与α之间的关系是确定的，即L的数值可以由式（7-35）计算出来。由于前面已导出一些壳体的M_b计算公式，所以对前面介绍的五种特定壳体，可以直接利用M_b的公式计算各自的回转半径。

将式（7-36）代入式（7-34）和式（7-33）的第3式，可求其他危险截面的弯矩。

比较式（7-36）、式（7-37）和式（7-38）可知，对于图7-10所示的壳体，由于b≤r_c≤a，所以M_b是最大弯矩，是正值（a>L），M_a是最小弯矩，是负值（b<L），M_c是中间值。如果壳体中存在r_c>a（如矩形壳体），则M_c是最大弯矩。引入回转半径L（相当于平均半径），其最大弯矩、最小弯矩的位置及大小更为直观，并易于确定。

到目前为止，并没给积分计算提出更方便的方法，如利用式（7-35）确定L值，显然要积分；如利用式（7-36），则必须先积分以便求得M_b。下面介绍一种近似计算方法，这种方法不用积分，它与精确解的误差不大，所以是工程上常用的方法。