圆角矩形容器设计技巧

带圆角的矩形壳体及其受力简图如图7-5所示。

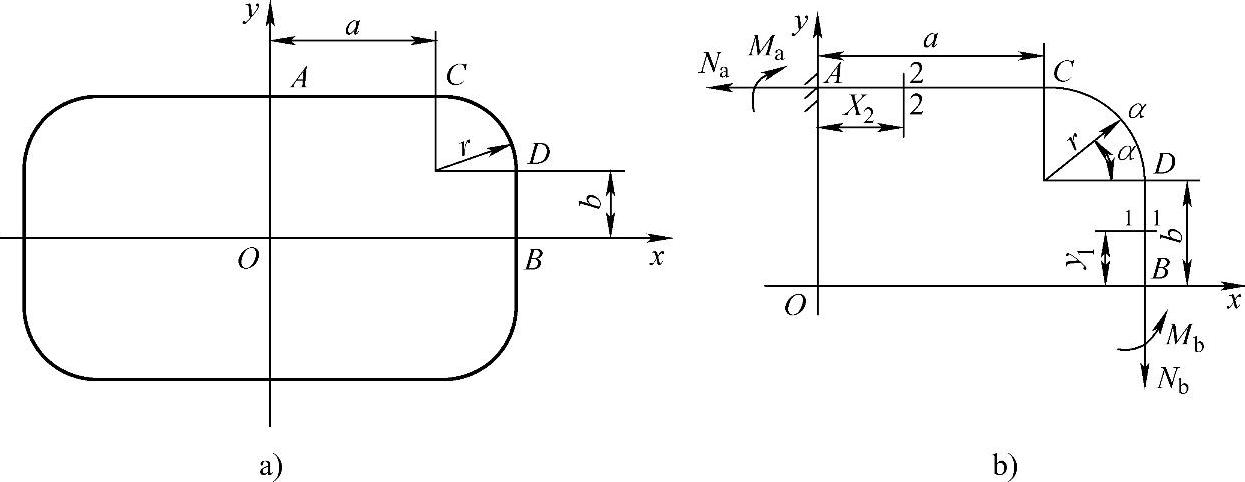
图7-5 带圆角的矩形壳体及其受力简图

设无限长的矩形截面的柱壳，尺寸如图7-5a所示。壳体的厚度为S，承受的内压力为p，现研究单位长度的一段柱壳，由于截面对称于x轴和y轴，所以其1/4，即ACDB段可以代表整个壳体。为了分析方便，这里假定a>b。

同样，1/4段的单位长度的壳体可简化为以A为固定端，B为自由端的悬臂曲梁。该梁的内侧受有介质压力p。由于截面A、B均在对称轴上，所以A、B两截面上的转角和横剪力均为零，按静力平衡条件可得

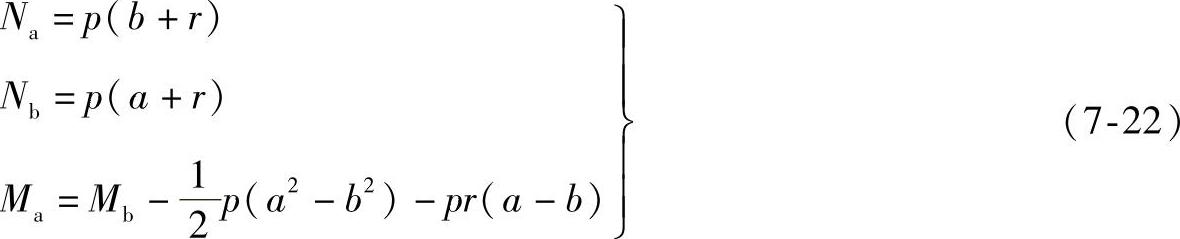
显然，式（7-22）中最后一个方程解不出两个未知量M_a和M_b。这里也需要用单位载荷法求解截面B的弯矩M_b。

由于曲梁AB由3部分组成，即水平梁AC，圆弧梁CD和竖直梁BD，这3部分的内力矩规律不同，积分式应分列成3个部分。由于剪力对内外壁应力的影响很小，因此略去剪力的影响。

3段梁的内力可由图7-6所示的静力平衡条件求得：

BD段的截面1（0≤y₁≤b）

N₁=N_b （7-23a）

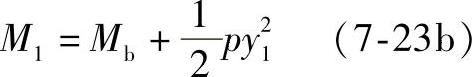
DC段截面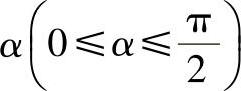

N_α=p（r+acosα+bsinα）

（7-23c）

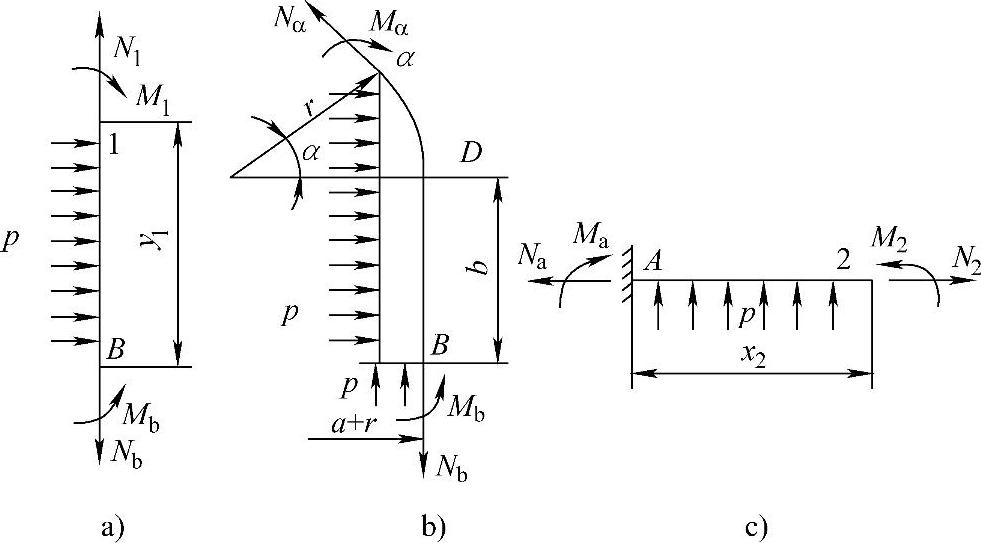
图7-6 内力计算简图

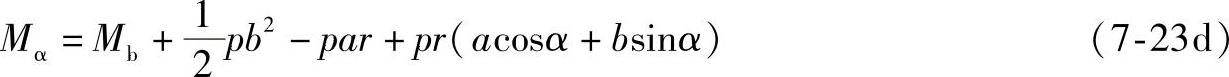
AC段截面2（0≤x₂≤a）

N₂=N_a（7-23e）

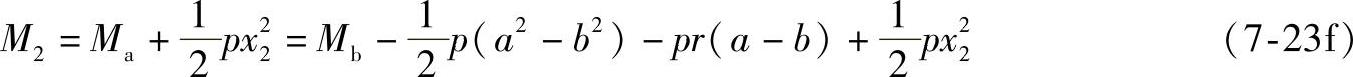(www.xing528.com)

根据梁AB的形状，式（7-9）由三部分组成，即

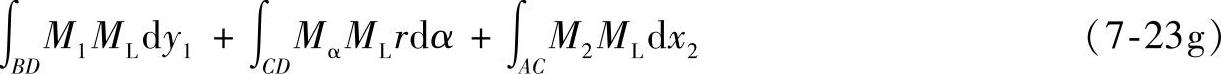
将M₁、M_α和M₂代入式（7-23g），并整理得

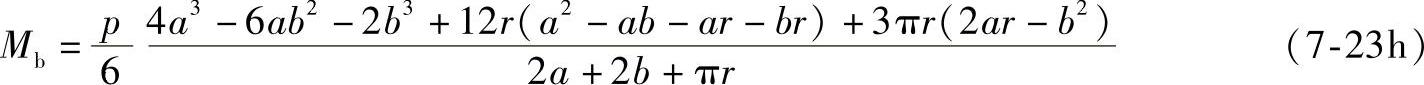
M_b求出后，可以利用相应的公式计算M_a、M₁、M_α及M₂了。由于内力公式比较复杂，为了寻求危险截面，所以对内力作如下分析。首先分析法向力，在a>b的情况下，N₁>N₂，而N_α有极值。为了求取极值可使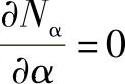，即

-asinα+bcosα=0

得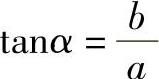，将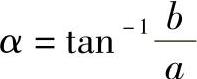带入式（7-23c），可得N_α的极大值为

再分析弯矩，式（7-23d）有极值点，将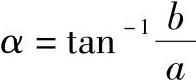代入式（7-23d）得最大弯矩为

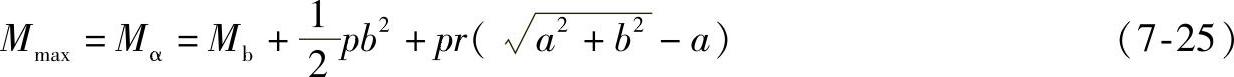
比较式（7-23b）、式（7-23d）及式（7-23f），可知最小弯矩为M_a，最大弯矩是M_α。

于是危险截面是弯矩最大的α截面和弯矩最小的A截面。

例3 已知带圆角的矩形壳体尺寸a=400mm，b=280mm，r=100mm，S=28mm，壳体的介质压力p=0.25MPa。试计算该壳体的危险应力。

解：由于危险截面是A截面和α截面，这里仅计算这两个截面的应力。

（1）内力

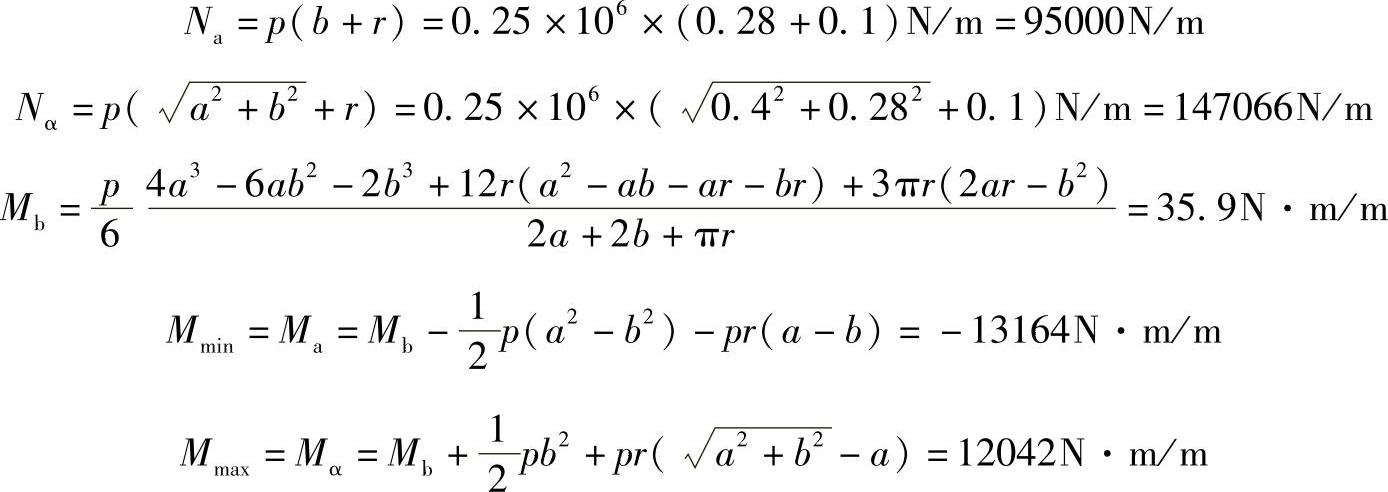
（2）应力

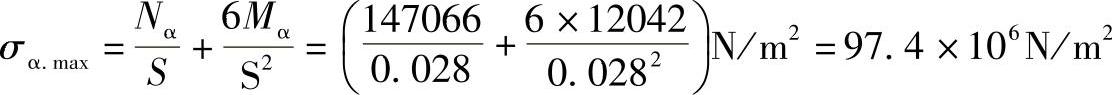
这里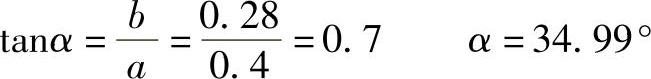

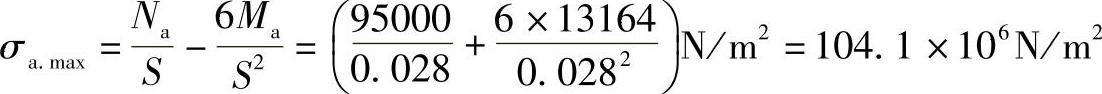
这里截面A是危险截面，弯曲应力比薄膜应力大得多。