例1 椭圆形柱壳的长轴半径a=500mm,短轴半径b=250mm,内压力p=0.25MPa,工作温度t=150℃,材料为20R,其[σ]t=126MPa,弹性模量E=2.0×105MPa,泊松比μ=0.3。试计算该壳体的壁厚和截面A、B的变形。
解:根据b/a=0.5,由表7-1查得
E(k)=1.2111 G(k)=0.7024
A(k)=1.2092 B(k)=0.3546
C(k)=0.8546 D(k)=0.2432
M(k)=1.5207 N(k)=0.3099
O(k)=0.6901 P(k)=0.2758
根据式(7-11),有

根据式(7-1)、式(7-2)和式(7-3),有

显然截面B的应力具有最大值,若取S=22mm,则
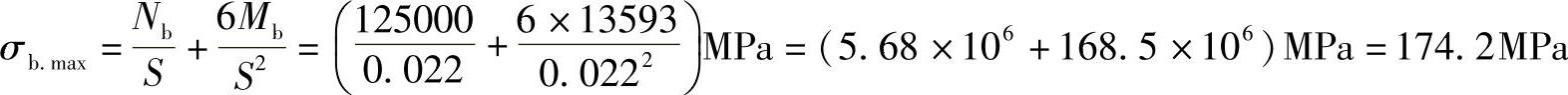
由于壳体的最大应力小于许用应力[σ]m=1.5[σ]t=189MPa,所以假定的壳体厚度S=22mm是合适的,考虑到壁厚附加量C=4mm,所以椭圆形柱壳的实际厚度Sc=26mm。
壳体截面A与B的变形可用式(7-17)及式(7-20)计算,其中

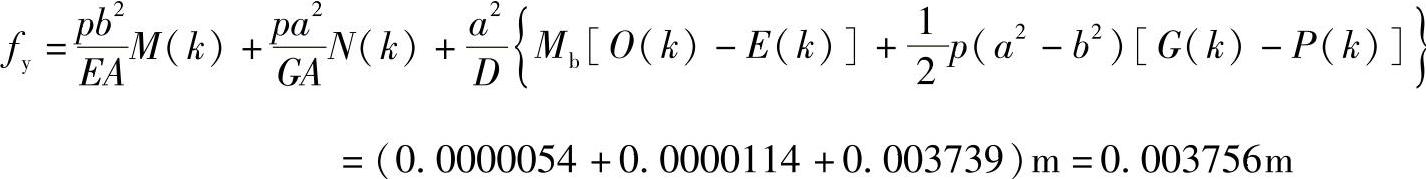
fx中负号表示位移与单位力Q0=1的方向相反,fy中正号表示B点位移与单位力N0=1的方向相同。
从例1可以看出弯曲应力比沿壁厚均布的拉应力(即薄膜应力)大得多,所以在可能的情况下应做成圆筒形壳体或回转壳体,这样可以节省材料(如1m直径的圆筒,在相同的情况下,强度要求的壁厚仅为1.08mm)。从变形计算可知,弯矩引起的位移比法向力与横剪力引起的位移大得多,只计算由弯矩引起的位移已足够精确。而且在弹性的范围内,壳体的变形量是很小的。(https://www.xing528.com)
例2 设圆筒直径Di=1600mm,设计压力p=1.0MPa,筒体壁厚(暂不考虑壁厚附加量)S=10mm。由于制造原因,筒体的椭圆度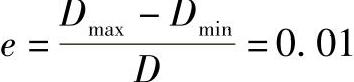 ,试计算此时壳体中的最大应力。
,试计算此时壳体中的最大应力。
解:理想圆筒形壳体的环向应力为

当出现椭圆度后,假定柱壳为理想椭圆形截面,中间面的平均直径D=1610mm,取
Dmax-Dmin=0.01Di=0.01×1600mm=16.0mm
假定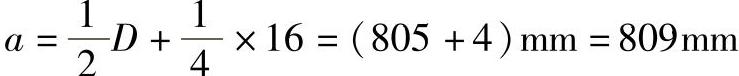

由b/a=801/809=0.9901,查表7-1得
E(k)=1.5631 G(k)=0.7835
由式(7-11)得

由式(7-3)得
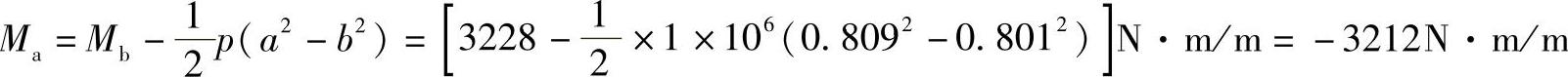
由式(7-1)及式(7-2)得

由式(7-12)及式(7-13)得

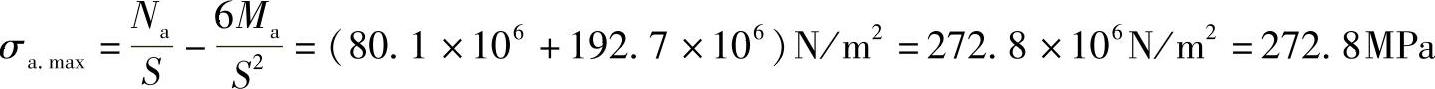
由本例可知,内压圆筒制造的椭圆度为e=0.01时,将产生比薄膜应力大得多的弯曲应力。如果总应力过大而产生塑性变形,则此时a、b的数值将变化,其应力自动降到允许的范围(指壳体材料具有良好的塑性)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




