图7-1所示的壳体,在内压力p的作用下要作趋向于圆的变形。这里仅分析中间面的变形。由图7-1可知最大变形发生在A点和B点。B点的收缩位移可简化为图7-2所示悬臂曲梁自由端B点的x向位移;A点的半径扩张可转化为B点的y向位移,它们同样可用单位载荷法求取。如果在B点作用x向单位力Q0=1(图7-4a),由Q0=1求得悬臂曲梁任意点C的内力,将此内力代入式(7-4),即可求得B点的x向位移。同理在B点作用的y向单位力N0=1,则可求得B点的y向位移。
1.B点的水平位移
若在悬臂曲梁的自由端B点作用有假想的单位力Q0=1,如图7-4a所示,此时任意点C的内力为
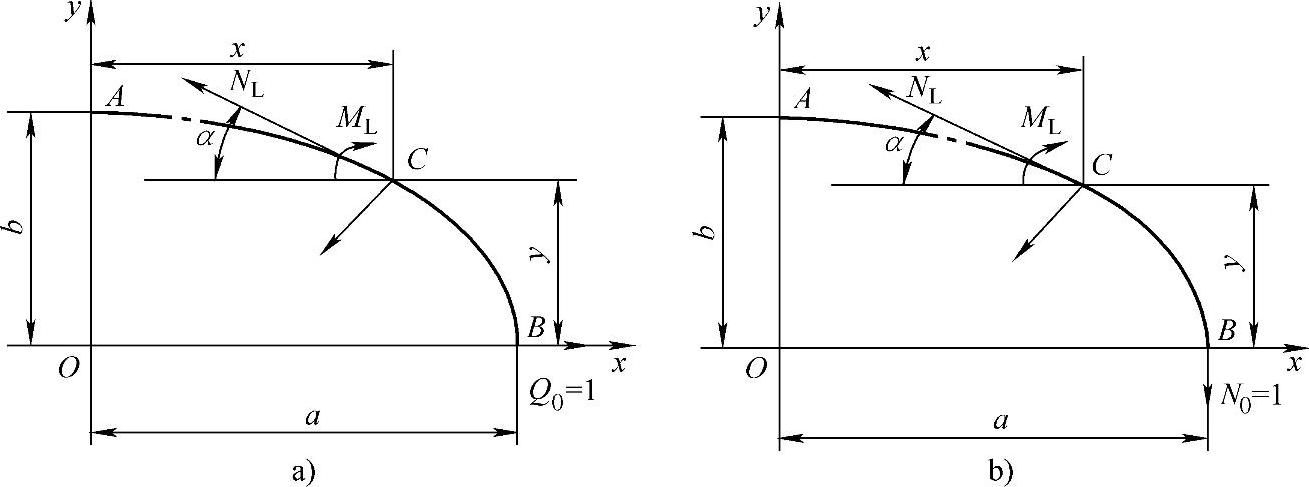
图7-4 单位载荷作用下曲梁中的内力

根据式(7-4),并考虑到壳体是双向应力状态,用板状刚度D代替公式中的抗弯刚度EI,对于等厚度的壳体,式(7-4)可写为
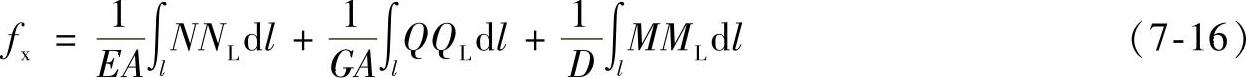
将式(7-5)、式(7-6)、式(7-7)、式(7-10)和式(7-15)代入式(7-16),经整理得
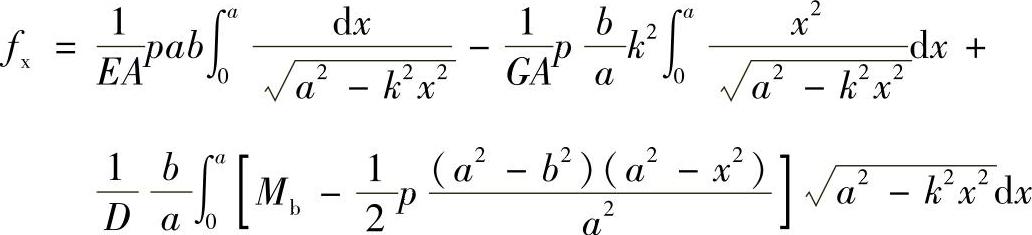
令x=az,dx=adz,有
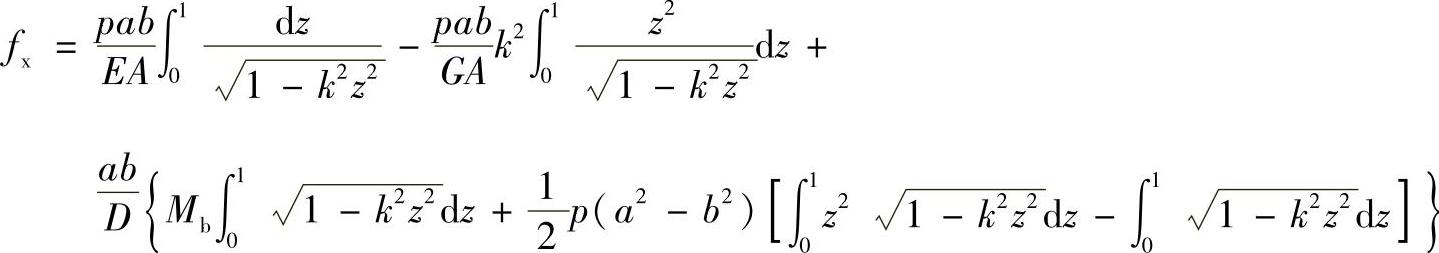
令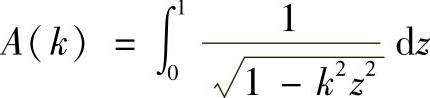
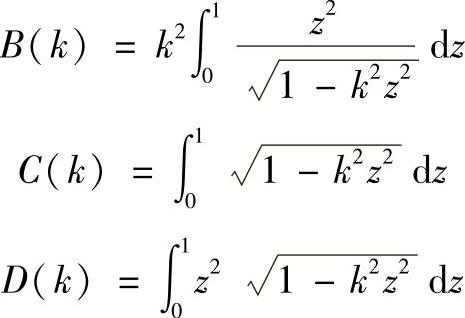
于是
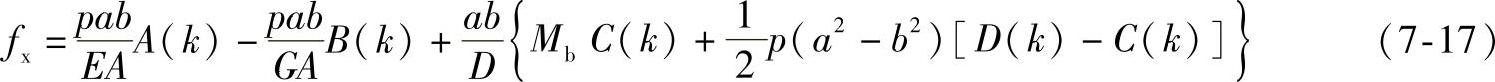
式中 p——壳体内介质压力(N/m2);(https://www.xing528.com)
a、b——分别为椭圆形壳体的长轴半径和短轴半径(m);
EA、GA、D——分别为抗拉刚度、抗剪刚度和板状刚度;
A(k)、B(k)、C(k)、D(k)——计算系数,它取决于椭圆的离心率k,可以用积分公式计算,也可以从表7-1中查取;
Mb——截面B的弯矩,由式(7-11)计算。
对于薄壁壳体和一般的梁,由弯矩引起的位移是主要的,若略去法向力N和横剪力Q对变形的影响,则水平位移的计算公式可简化为或
2.B点的竖直位移
如果在悬臂梁的自由端B点作用有单位法向力No=1(图7-4b),则可用单位载荷法求得B点的竖直位移。在B点作用单位力No=1后,曲梁任意点C的内力为

将式(7-5)、式(7-6)、式(7-7)、式(7-10)及式(7-19)代入式(7-4),同样用板状刚度D代替抗弯刚度EI,整理后得
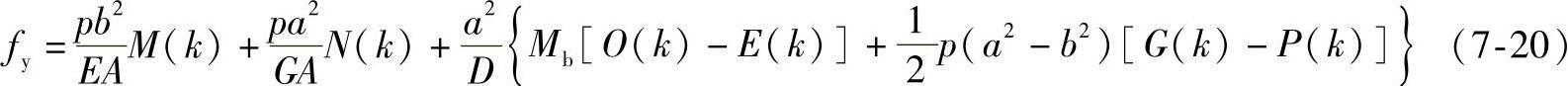
式中 M(k)——计算系数,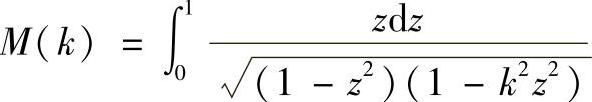 ;
;
N(k)——计算系数,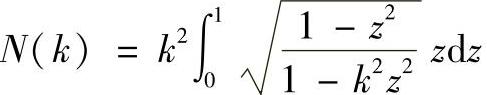 ;
;
O(k)——计算系数,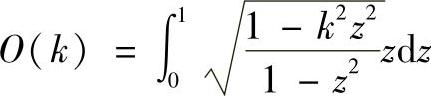 ;
;
P(k)——计算系数,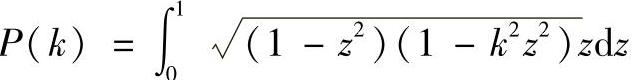 。
。
对于薄壁壳体和一般的梁,只计算由弯矩引起的位移已能满足精度要求,此时
或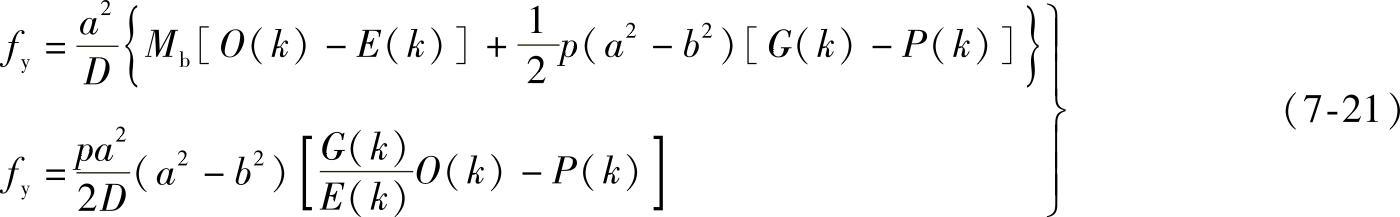
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




