危险截面和综合应力分析

无限长的椭圆形截面柱壳，只需考虑以上公式所计算的环向应力即可。而对于有限长的容器，不仅有环向应力，还有轴向应力。在一般情况下，轴向应力比环向应力小得多，可以不

计算。

由式（7-7）

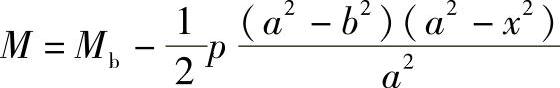
可知：

当x=a时，M=M_b；

当x=0时，

；

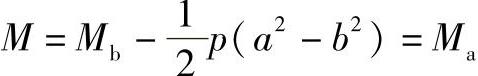
当0≤x≤a时，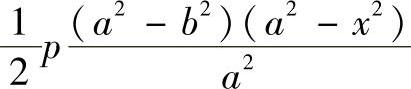

总是正值，而且随x的增大而减小。由此可知，截面B的弯矩M_b具有最大值，而截面A的弯矩M_a具有最小值，而且是连续变化的，即

M_a≤M≤Mb

由式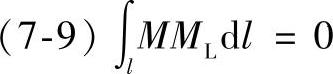

可知：

M_L=1，dl总是正的，则M的数值有正有负。显然M_b是正弯矩，M_a是负弯矩，而且M_a是负弯矩中绝对值最大者。由于未确定M_b及M_a中何者为最大，所以两个截面的应力必须同时检验。即

截面B的内壁应力：

(www.xing528.com)

截面A的外壁应力：

式中　N_a、N_b——分别为截面A、截面B单位长度的法向力（N/m）；

M_a、M_b——分别为截面A，截面B单位长度的弯矩（N·m/m）；

S——扣除壁厚附加量的壳体壁厚（m）；

[σ_m]——壳体材料的允许应力（N/m²）。

非圆形截面壳体中的弯曲应力比由法向力引起的沿壁厚均匀分布的拉应力大得多，考虑到应力分类及其检验条件，建议：如果壳体要控制变形量（如闸阀），即壳体与内件有配合关系时，取[σ_m]=[σ]^t，一般均取[σ_m]=1.5[σ]^t；如果容许有较大的塑性变形（如一般容器与管道），可取[σ_m]=3[σ]^t。这里的许用应力[σ]^t可按压力容器的设计规定选取。

如果需要计算轴向应力，则可用下面的计算方法计算。

轴向应力由两部分组成，一部分为沿壁厚均匀分布的拉应力，这可借助于圆筒的轴向应力公式。另一部分系由环向弯曲应力的轴向约束而产生的轴向弯曲应力，即

σ_z.max=σ_z.L+σ_z.W=σ_z.L+μσ_W （7-14）

式中　σ_z.L——沿壁厚均匀分布的轴向拉应力，

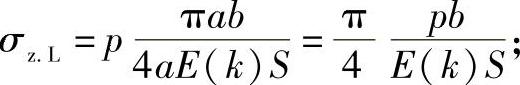
E（k）——计算系数，由表7-1查取，其中4aE（k）为椭圆周长；

σ_z.W——轴向弯曲应力（N/m²）；

σ_W——环向弯曲应力，为；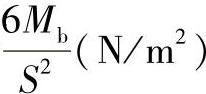

μ——泊松比。