椭圆形曲梁内力分析与计算

由于截面A、B在对称轴上，所以该截面的横剪力等于零，只有法向力和弯矩。这里N_a、N_b为法向力，以拉为正；M_a、M_b为弯矩，以内壁受拉应力为正。外载荷p作用在壳体内壁上，即曲梁内侧，也可简化为作用在Oy轴上和Ox轴上，如图7-2所示。

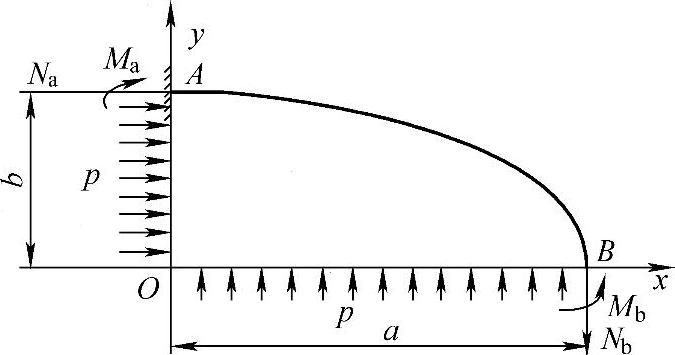
图7-2 椭圆形壳体的受力简图

根据平面问题的力平衡条件可得

N_a=pb（7-1）

N_b=pa（7-2）

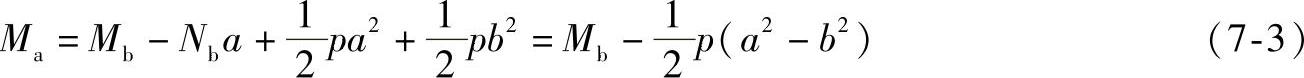
这3个方程式解不出4个未知量N_a、N_b、M_a和M_b，它属于静不定问题。这里借助于单位载荷法列补充方程。

单位载荷法的基本方程式为

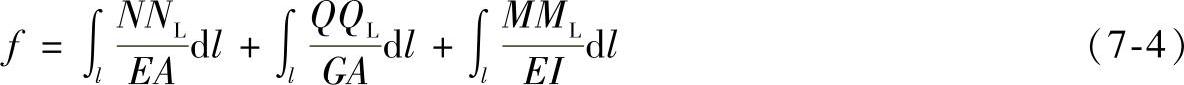
式中 f——截面B的位移，它可以是转角θ，也可以是线位移f_x、f_y，这要取决于作用在截面B上的单位载荷；

N、Q、M——分别为外载荷p作用下梁内任意点的法向力、剪力和弯矩；

N_L、Q_L、ML——分别为作用在截面B上的单位载荷所产生的梁内任意点的法向力、剪力和弯矩；

EA、GA、EI——分别为曲梁的抗拉刚度、抗剪刚度和抗弯刚度；

dl——梁的微元长度（积分要遍及全梁）。

曲梁内任一点的内力如图7-3所示。

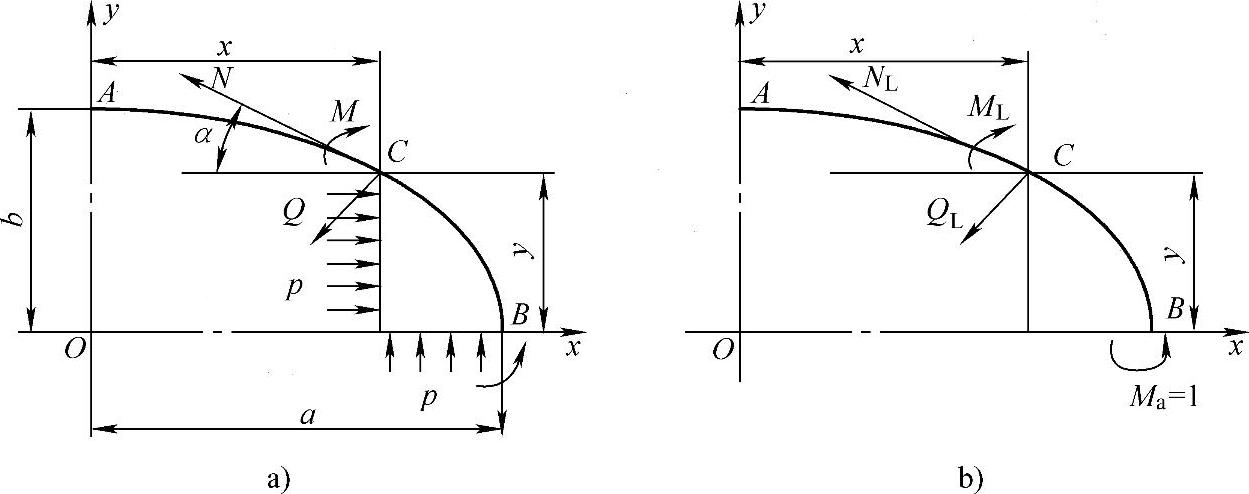
图7-3 曲梁内任一点的内力

由图7-3a的力平衡条件，可求得由介质压力p所产生的曲梁AB内任意点C的内力，它们分别为

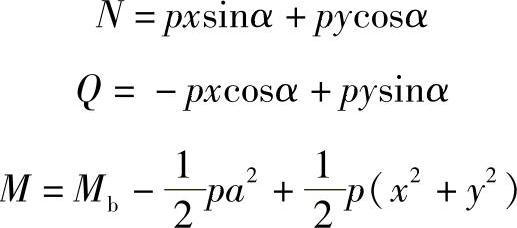
上述公式中出现了3个椭圆的参数x、y和α，其中只有1个是独立的，现在以x作为变量，其他参数看作是x的函数，并在公式中消去，以便公式中仅用1个变量。由椭圆方程

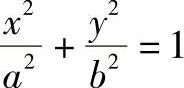
对图7-2所示的曲梁来说，x、y均为正值，得。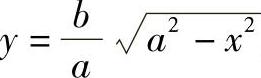

式中 a、b——分别为椭圆的长轴半径和短轴半径；

x、y——任意点C的坐标，其中0≤x≤a，0≤y≤b。上式对x取导

由图7-3可知

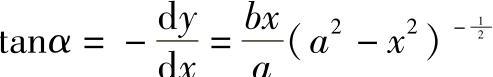
又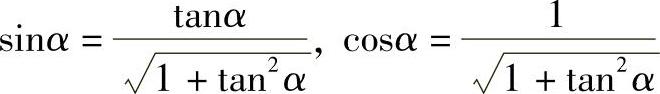

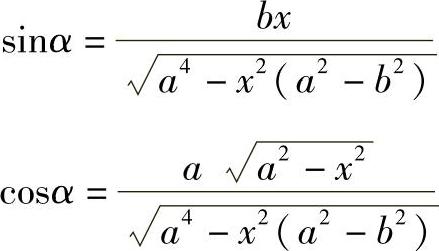
将上述关系式代入任意点C的内力公式中，经整理可得

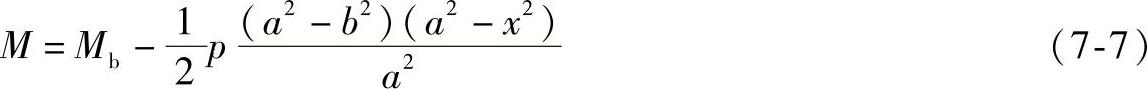(https://www.xing528.com)

由图7-3b的力平衡条件，可求得由单位力矩M₀=1所引起的任意点C的内力，它们为

将式（7-8）代入式（7-4），可得截面B的转角

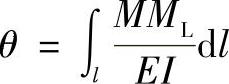
考虑到梁为单向应力状态，而板、壳系双向应力状态，用板状刚度D代替上式中的抗弯刚度EI，有

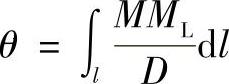
式中 D——板状刚度，可用下式计算：

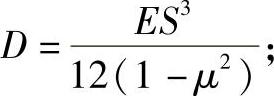
E——壳体材料的弹性模量（N/m²）；

S——壳体厚度（m）；

μ——泊松比。

对于等截面的梁或等厚的壳体，D=常数，所以：

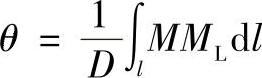
考虑到截面B对称于x轴，其转角θ_b=0，于是：

式中 dl——曲梁的微元长度，它可写为

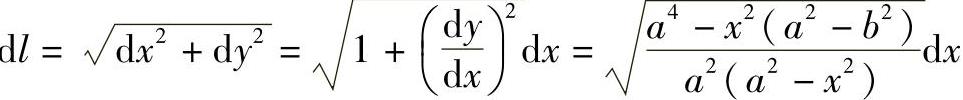
在公式中引入椭圆的离心率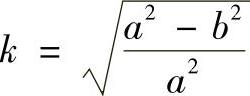，则

将式（7-7）、式（7-8）、式（7-10）代入式（7-9），可得

令x=az，dx=adz，这里z是新的变量，于是上式可写为

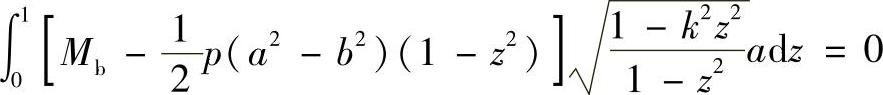
或

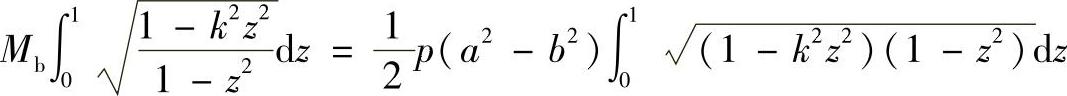
令

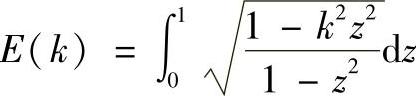
于是

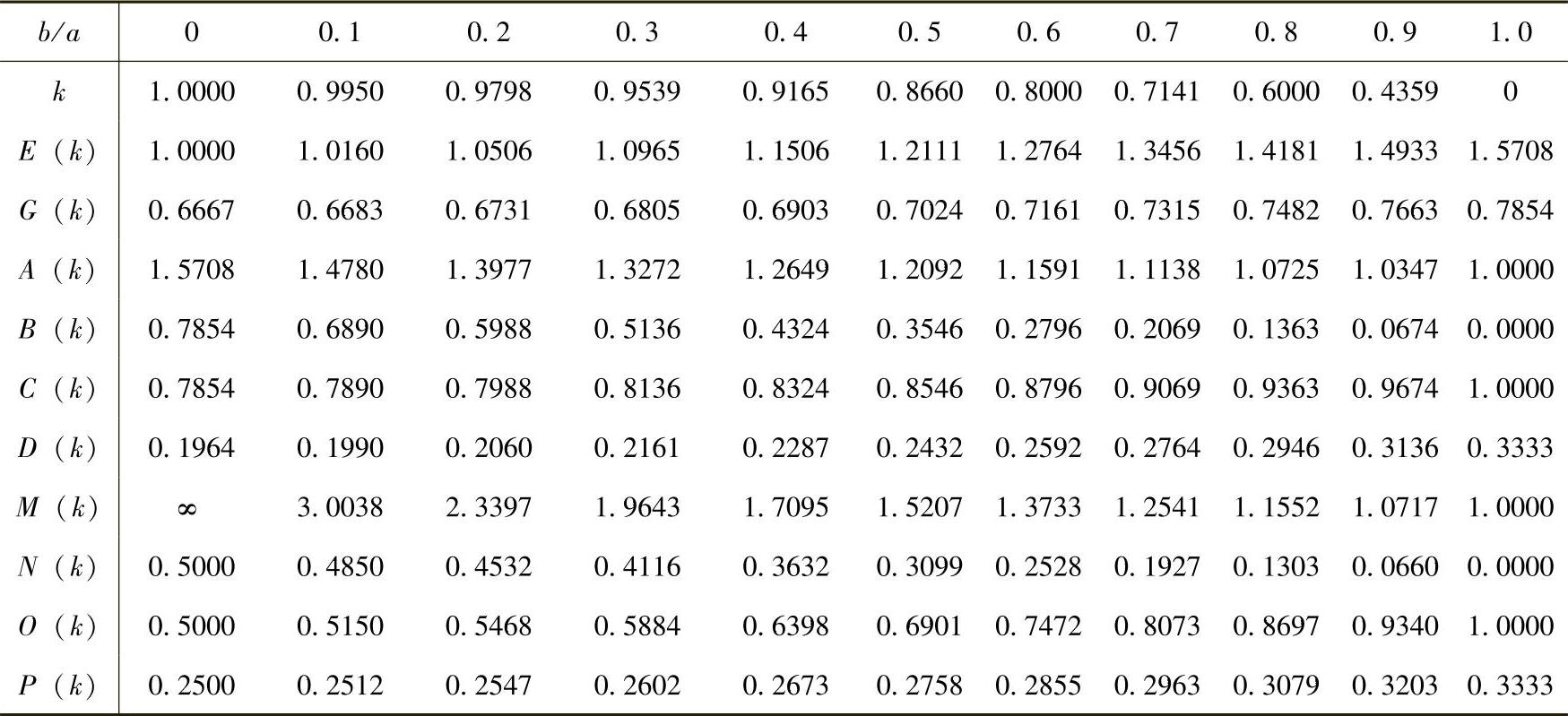
这里G（k）和E（k）可按前面的积分公式计算，两者都是椭圆离心率k的函数。表7-1列出了不同k值下的G（k）和E（k）的数值。当G（k）和E（k）查出后，可按式（7-11）计算M_b，有了M_b便可计算截面A的弯矩M_a和任意截面C的内力矩M。此时椭圆形曲梁的内力就全部解出了。

表7-1 椭圆形壳体的相关系数