开孔接管处应力集中优化

容器开孔接管部位的应力集中会造成壳体的强度削弱、不连续应力、局部应力、焊接缺陷和残余应力。开孔接管处的力学特征常用应力集中系数K_t来描述，即

式中 K_t——弹性应力集中系数；

σ——未开孔时的名义应力（最大薄膜应力）；

σ_max——开孔后按弹性方法计算出的最大应力（开孔边缘处最大应力）。

1.开孔的应力集中

（1）平板开小圆孔的应力集中

弹性力学中已有对无限板开小圆孔的集中应力的解，单向拉伸平板开小圆孔时的应力集中（板宽在孔径的5倍以上），孔附近任意点（r，θ）的应力分量为

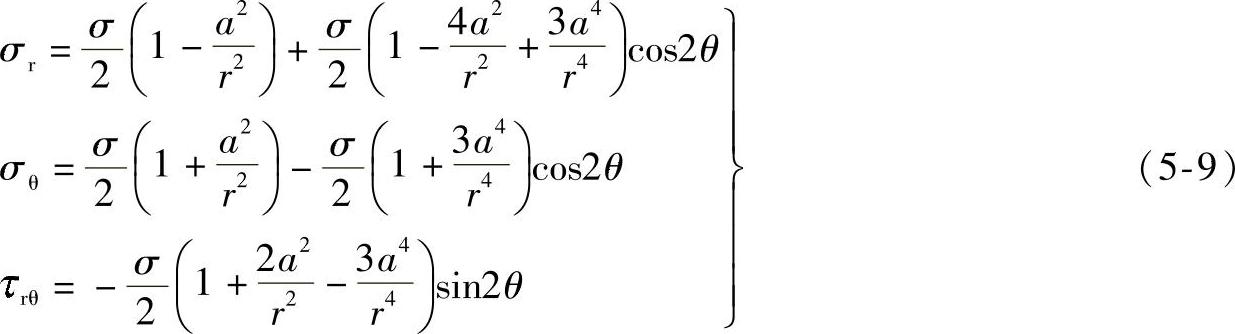
在孔边缘（r=a，其中a为孔半径）处：σ_r=0；σ_θ=σ（1-2cos2θ）；τ_rθ=0。当2θ=±π时（即θ=±π/2），σ_θ取极大值，即σ_θ︱_θ=±π/2=σ_max=3σ。所以，应力集中系数：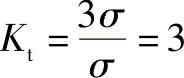

由此可见，平板开孔的最大应力在孔边θ=±π/2处，当r>a后应力便迅速衰减，表现出孔边应力集中和局部性的特点，如图5-9所示。

（2）薄壁球壳开小圆孔的应力集中

如图5-10所示，球壳受双向均匀拉伸应力作用时，孔边附近任一点的应力分量为

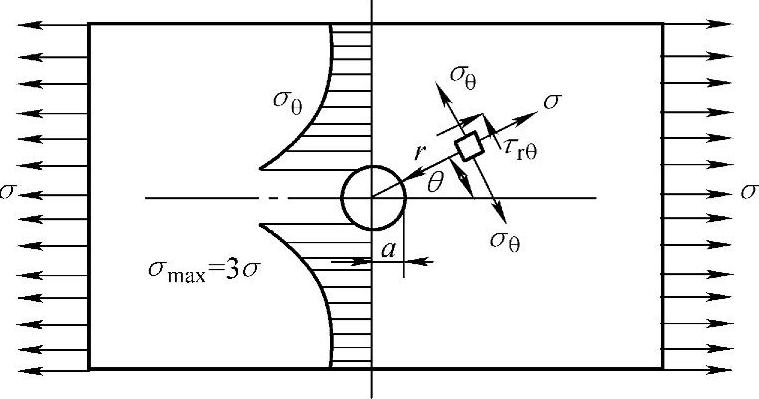
图5-9 单向拉伸平板开小圆孔的应力集中

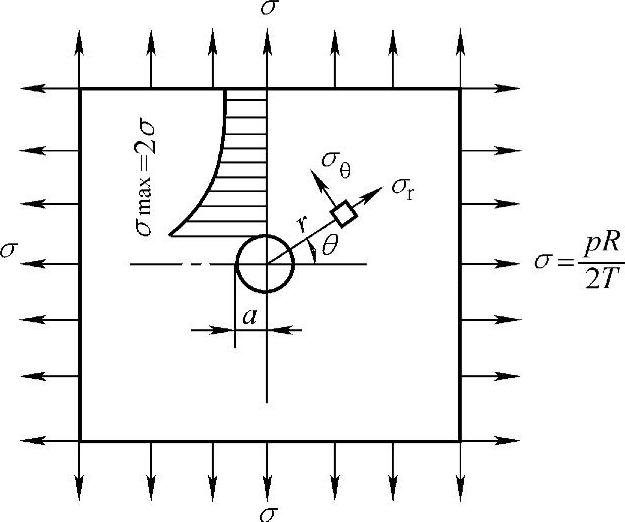
图5-10 球壳开孔的应力集中

在孔边（r=a）处：σ_r=0；σ_θ=2σ。则：孔边r=a处，σ_max=σ_θ=2σ，应力集中系数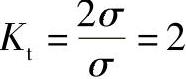

（3）薄壁圆柱开小圆孔的应力集中

如图5-11所示，薄壁柱壳受均匀内压作用，其孔边附近任意点的应力分量为

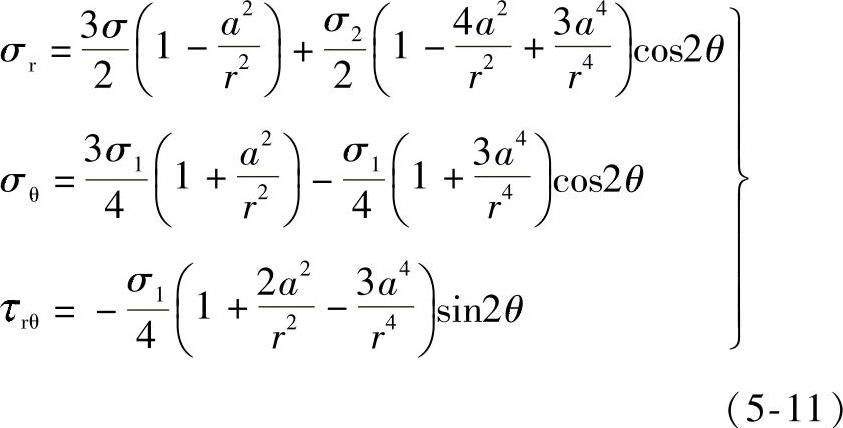
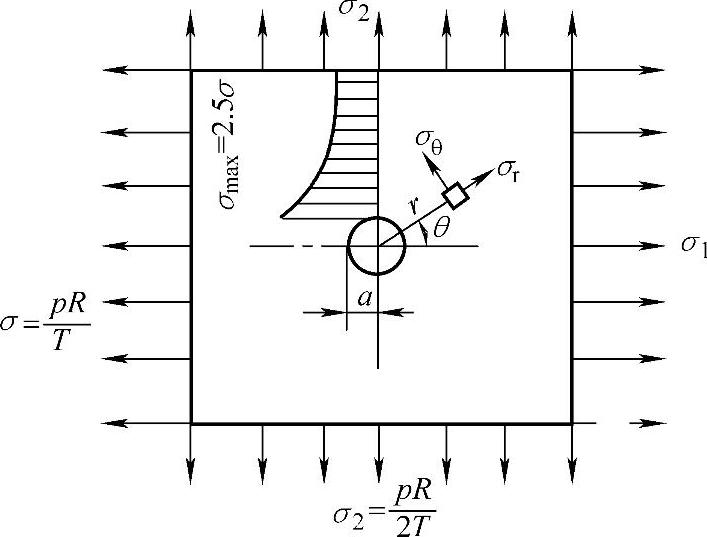
图5-11 圆柱壳开孔的应力集中

在孔边（r=a）处：σ_r=0；σ_θ=1.5σ₁-σ₁cos2θ=σ₁（1.5-cos2θ）；τ_rθ=0。当2θ=±π时，σ_θ取极大值，即σ_θ︱_θ=±π/2=σ_max=2.5σ₁。

1）孔边径向截面处的应力集中系数：

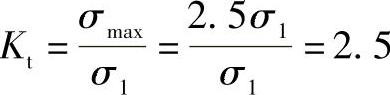
2）在另一截面，轴向截面的孔边θ=0及π时的最大应力：σ_max=σ_θ=0.5σ₁。此时的应力集中系数：

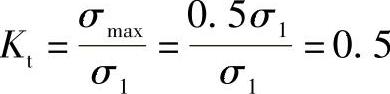
从以上计算结果可以看出，薄壁圆柱开小圆孔时，孔边经向截面的应力集中系数要比其轴向截面大得多。

通过以上三种典型开孔分析可知：

1）最大应力在孔边，孔边是应力集中最严重的地方。

2）孔边应力集中有局限性，并衰减很快。

2.开孔并带有接管时的应力集中

以上导出的是平板及壳体上开小圆孔引起的应力集中。若开孔处有接管连接，在内压作用下，壳体与开孔接管的连接处会出现变形协调而导致的不连续应力和附加弯矩。此外，由于容器的形状结构、承压状态和工作环境影响，它的受力比平板复杂，所以，在壳体开孔并带有接管的孔边缘出现的是多种应力叠加的较为复杂的应力状态，至今尚未有公认的解析解。目前的各种近似解也都是通过应力集中系数来表征。

球壳上开孔接管，如图5-12所示。图5-12a中虚线表示球壳与接管在内压作用下各自自由状态下的薄膜变形，变形前的A点在变形后球壳上应到B点，接管上应到C点。而在实际情况下如图5-12b所示，变形后A点同时到达D点，这就出现一个变形协调的过程。变形协调的结果如图5-12c所示，在球壳开孔处的边缘弯矩M₀和边缘剪力Q₀均会对壳体和接管端部产生附加弯曲应力。这种情况下的应力为局部应力，并很快衰减。最大应力是球壳开孔边外侧的环向应力，应力集中系数在2以上。

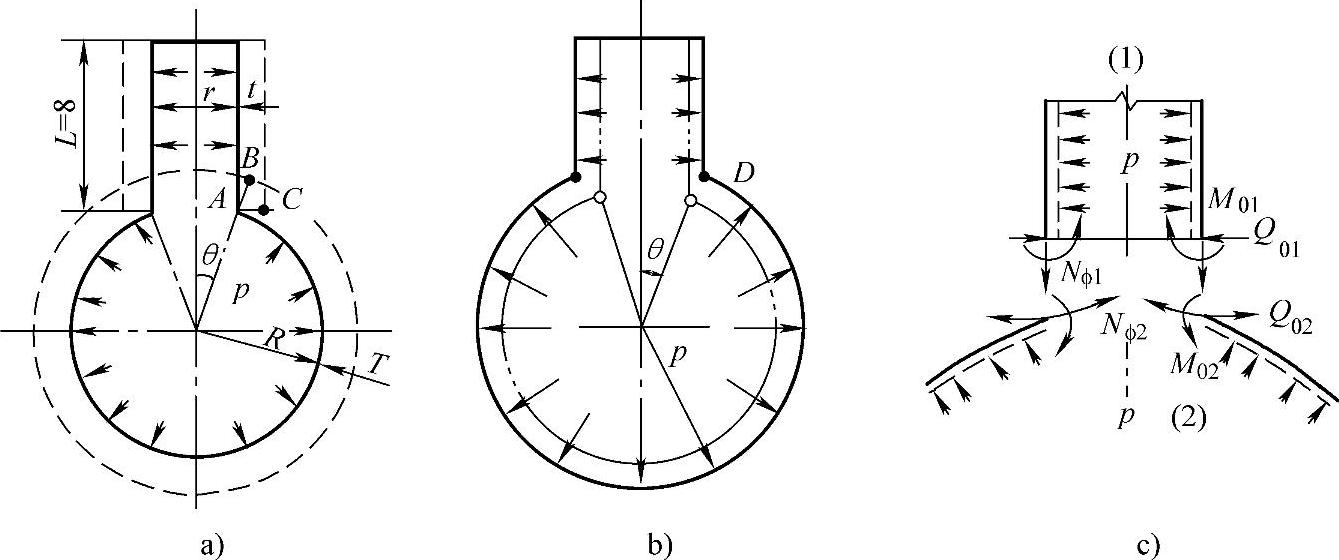
图5-12 球壳开孔接管处的变形协调与内力

3.应力集中系数的计算

在受内压的壳体上开孔并接管后，由于变形不连续会产生附加应力，另外还由于开孔带接管后，接管根部不等截面过渡（小圆角）而带来应力集中，以上这些应力想一一求解十分困难。

我们将以上原因所产生的接管部件的最大弹性应力称为应力峰值或集中应力。应力峰值与不开孔部位的薄膜应力之比称为弹性应力集中系数。下面介绍几种求解应力集中系数的方法。

（1）应力指数法

它是美国压力容器研究委员会在大量实验数据支持下的一种计算壳体和接管连接处最大应力的简易方法，它已被ASME Ⅷ-2篇、JIS B 8250及JB 4732—1995《钢制压力容器分析设计标准》所列入。它所考虑的接管处的三向应力包括：经向应力σ_t，径向应力σ_r，法向应力σ_n，如图5-13a所示。

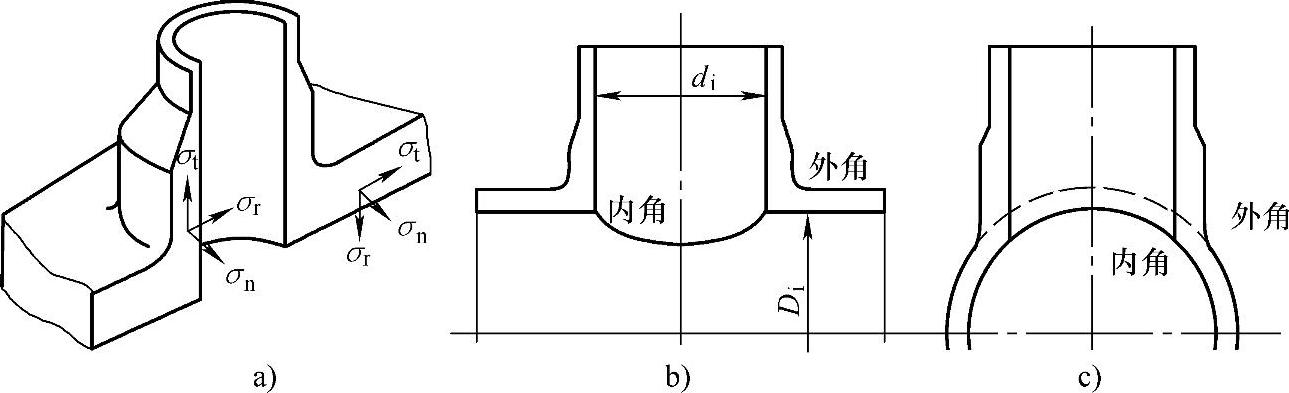
图5-13 单个接管连接处的各项应力分量定义及计算应力指数的位置

a）球形容器及凸形封头接管区的应力分量定义

b）圆筒接管的纵向截面 c）圆筒接管的横向截面

应力指数法仅适用于单个开孔接管。诸方向的应力中各有一最大值σ，该值用应力指数I表示为

1）对于球壳和成形封头，某一指定点的应力最大值：

(www.xing528.com)

2）对于圆柱壳，某一指定点的应力最大值：

式中 D_m——壳的平均直径（中径）；

p——内压；

t_n——名义厚度。

在我国JB4732中也推荐使用此工程计算方法，各应力指数来源于大量的实验数据和数值分析资料，对于开孔区的应力指数应按图5-13所示来定义各应力，指数I见表5-3。

表5-3 容器应力指数I示例

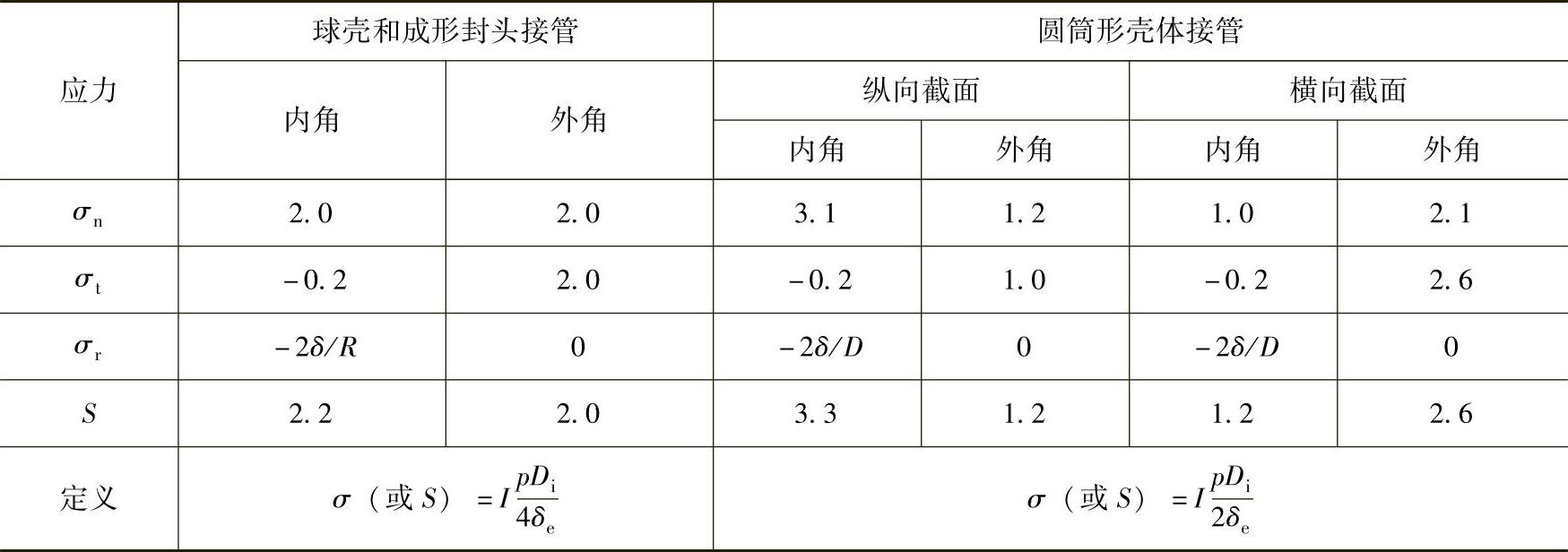
图5-13及表5-3中的符号含义：

σ_n——指定点的垂直于截面的法相应力分量；

σ_t——指定点的在截面内的且平行于截面边界的应力分量；

σ_r——垂直于截面边界的应力分量；

S——指定点的组合各应力分量的应力强度，S=σ₁-σ₃，其中σ₁为最大应力，σ₃为最小应力；

δ_e——壳体的有效厚度；

σ——指定点的应力分量。

用应力指数法求解指定点的最大应力及应力强度特别适用于工程设计中要做疲劳设计的容器，但应用该法时有以下限制：

1）该法仅适用于单个开孔接管，且D_i/t_n≤100，d_i/D_i≤0.5。

2）接管根部的内外侧均需按规范给出足够的过渡圆角及加强高度尺寸。

3）该法仅考虑受内压载荷时的应力集中。如有压力以外的载荷，如温度差、外力矩等引起的应力可以与压力引起的应力叠加，但必须注意所在部位和应力的方向。

4）该法不得用于接管区非整体补强及异种钢组成的补强结构。

从以上介绍可以看出，应力集中系数K_t与应力指数I具有相似的意义，但两者还是有所区别的。

①应力集中系数K_t更具有代表结构特性的含义，一个局部区域只有一个K_t值。K_t的大小可以衡量结构应力集中的优劣。

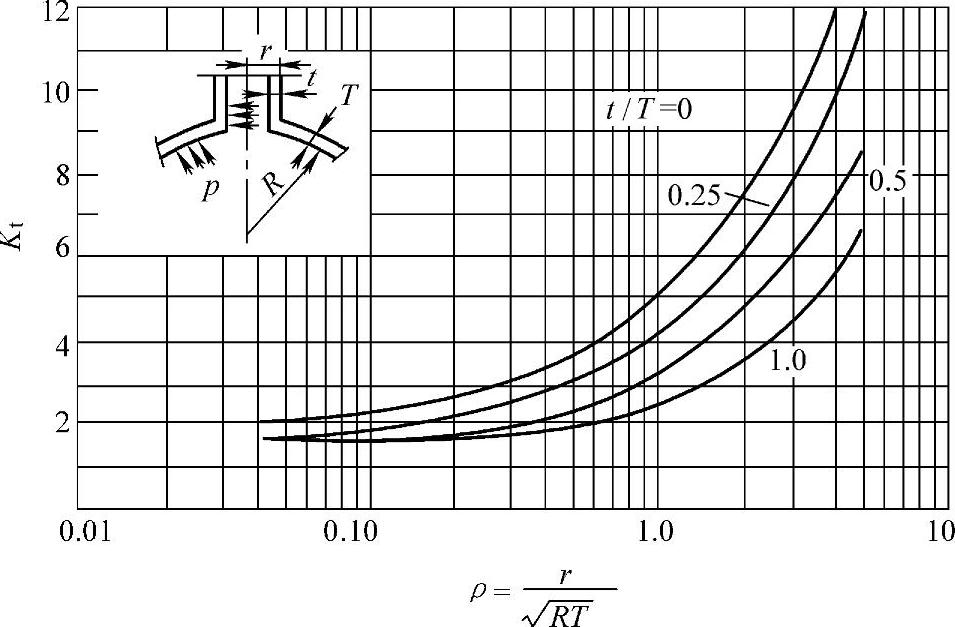
图5-14 球壳带平齐接管的应力集中系数曲线

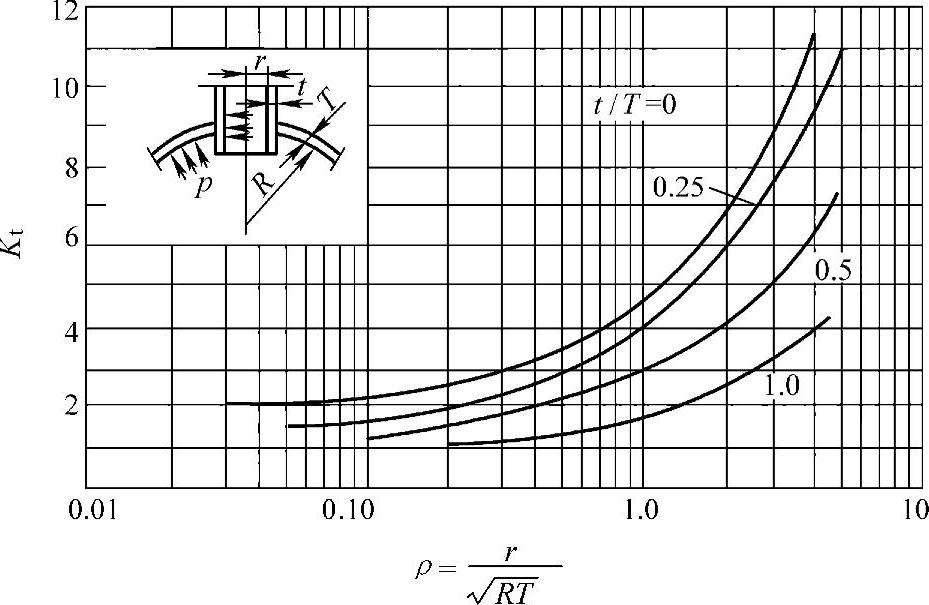
图5-15 球壳带内伸式接管的应力集中系数曲线

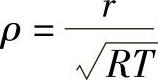
式中 r，R——接管与球壳的半径；

T——球壳厚度。

ρ仅反映了球壳开孔的影响，值越大，应力集中系数越高。而t/T反映的是接管的影响。

②应力指数I可以是多个（如拐角的内侧、外侧、不同方向），而且不一定是最大的。

（2）球壳开孔接管处应力集中系数曲线

为了便于计算，将不同直径、不同厚度的壳体，当它带有不同直径、不同厚度的接管时的应力集中系数按理论计算后，再结合大量的实验数据绘制成一组曲线。图5-14和图5-15所示就是球壳带平齐式接管和内伸式接管在内压作用下的应力集中系数图。图中采用了两个与应力集中系数有关的无因次结构几何参数，一个是开孔系数ρ，另一个是t/T。其中：

由图可知，当ρ越大，即开孔直径越大时，应力集中系数越高。相反，减小孔径，增大壳壁厚度均可降低应力集中系数。另外，内伸式接管的应力集中系数较低，尤其当内伸接管壁厚较厚时能有效的降低应力集中和补强。

上述应力集中系数曲线有一定的适用条件：

1）当r/R过小或过大时，应力集中系数曲线均会有较大的误差。

2）当R/T过小，即壁厚过厚，应力沿壁厚分布的不均匀性增大，应力集中系数明显比图示值减小；而当R/T过大，即壁厚太薄，不连续效应施加给壳体的附加弯曲效应更为明显，使K_t值明显增大。因此使用应力集中系数曲线时必须满足以下两个适用条件：

（3）椭圆形封头开孔的应力集中系数

椭圆形封头开孔的应力集中系数可以近似的采用上述球壳开孔接管的曲线，只要将椭圆中心处的曲率半径折算为球的半径即可。

R_i=K₁D_i（5-16）

式中 K₁——修正系数（见表4-2）；

D_i——椭圆封头的内直径；

R_i——折算为球壳的当量半径。

（4）圆筒开孔接管及其他情况的应力集中系数

圆筒上的开孔接管应力集中系数可采用上述球壳开孔接管的曲线近似的用于圆筒上，也有一些经验曲线可使用，如图5-16所示。

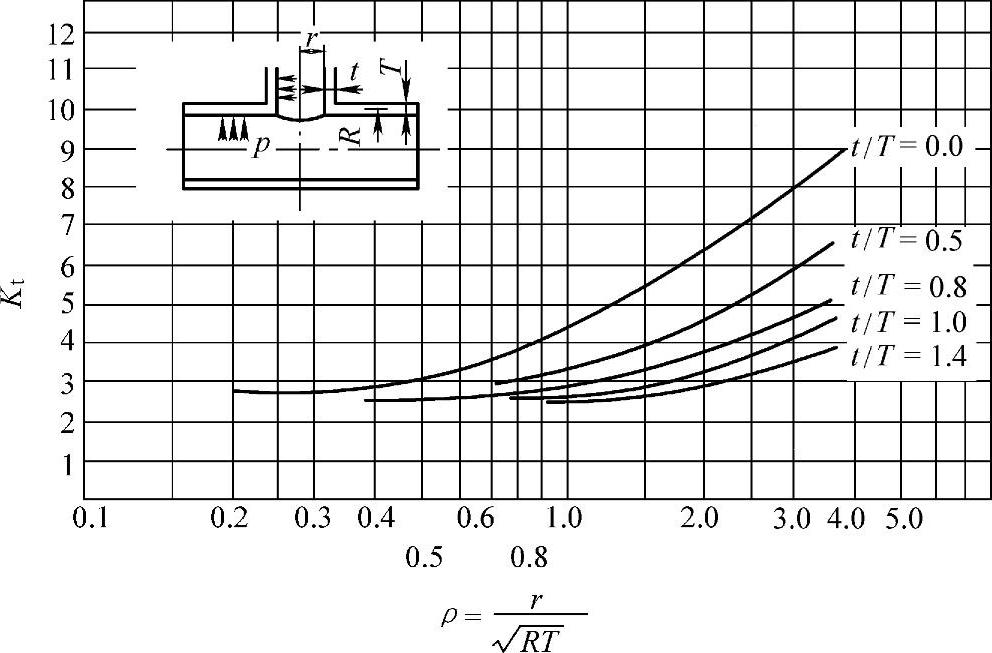
图5-16 圆柱壳开孔接管的应力集中系数曲线

当球壳或圆筒上的接管上作用有轴向力、剪力或弯矩时，可先求出各自的最大应力，再进行代数叠加而得到。