外压封头和球壳的稳定性计算

外压封头的形式主要有凸形封头和锥形封头两种，其中凸形封头的形式主要包括半球形封头、椭圆形封头和碟形封头等。这些封头的主要应力是压应力，故与筒体一样也存在稳定性问题。封头的失稳分析比圆筒复杂得多，因此在设计中仍采用一些近似方法，如以弹性失稳为基础，结合实验数据给出半经验临界压力计算式，再取近似值。外压球壳的计算与凸形封头中半球形封头的计算完全一样。

1.外压凸形封头

（1）半球形封头

1）半球形封头的临界压力。

按照弹性稳定理论，对于受均匀外压的球壳，其临界应力与同厚度、同半径的受轴向压缩圆柱壳相同。这样按小挠度弹性稳定理论，受均布外压球壳的临界压力经典公式为

对于钢材，取μ=0.3代入式（4-20）得：

式（4-21）即为经典小挠度解。

1939年Karman和钱学森采用非线性大挠度理论，导出下列临界压力值：

但通过实验得到的临界压力平均值为

取m=3和R≈R₀（用t_e代替t），得

式中 [p]——许用外压力（MPa）；

E——材料弹性模量（MPa）；

R₀——球壳外半径（mm）；

t_e——球壳有效厚度（mm）。

式（4-24）即为半球形封头或球壳的弹性失稳计算式。但设计时用图算法也比较简单，且可扩大到非弹性失稳计算。

2）半球形封头图算法原理。在球壳的设计中，首先定义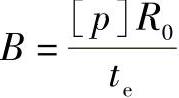，因为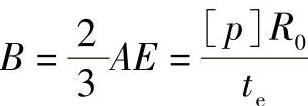，故代入式（4-24）中得：

于是

3）图算法计算外压半球形封头的过程：

①假设壁厚t_n，计算t_e=t_n-C。

②按式（4-25）计算出A。

③按所用材料，查外压应力系数选用表4-1确定对应的外压应力系数B曲线图，再按对应的外压应力系数B曲线图4-8～图4-14，由A值向上引垂线，查B值。若A值落在材料温度线左方，则直接按式（4-24）计算出[p]。

④按式（4-26）计算许用外压[p]。

⑤比较计算压力p_c与许用外压[p]，要求p_c≤[p]且比较接近。

（2）外压碟形和椭圆形封头的计算

外压碟形和椭圆形封头的计算可以直接用外压球形封头设计计算公式进行计算，只是需对公式中个别参数进行调整。

1）外压碟形封头。

对于碟形封头，过渡区承受拉应力，仅球冠部分为压应力，有发生失稳的可能性，因此以球冠的外半径作为计算半径R₀。(www.xing528.com)

2）外压椭圆形封头。

对于椭圆形封头，取当量球壳计算外半径R₀=K₁D₀来计算，系数K₁可由表4-2查得（对于标准椭圆形封头a/b=2，由表4-2可知：K₁=0.9）。

表4-2 系数K1

2.外压锥形封头

圆锥壳受均布外压的稳定性问题是一个很复杂的问题，因此在工程上还需要依靠大量的实验数据。

（1）半锥角α≤60°的外压锥形封头

在实验中发现，锥壳的失稳类似于一个等效的圆柱壳失稳，锥壳大端直径（D_L）和小端直径（D_S）之比对失稳影响很大。等效圆柱的高度等于锥壳的母线长度（L_x），而等效圆柱的半径等于锥壳两端第二曲率半径的平均值，因此锥壳的临界压力可表示为

式中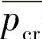——等效圆柱壳的临界压力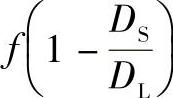；——与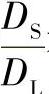有关的函数，

对于α≤60°的外压锥形封头，按承受外压的等效圆柱形筒体计算。变换式（4-9）后可得锥壳的临界压力为

式中 L_ε——等效圆筒长度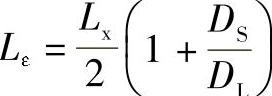，，L_x的取法如图4-15所示；

D_L——锥壳大端外直径；

D_S——锥壳小端外直径；

t_ε——等效圆筒壁厚，t_ε=tcosα。

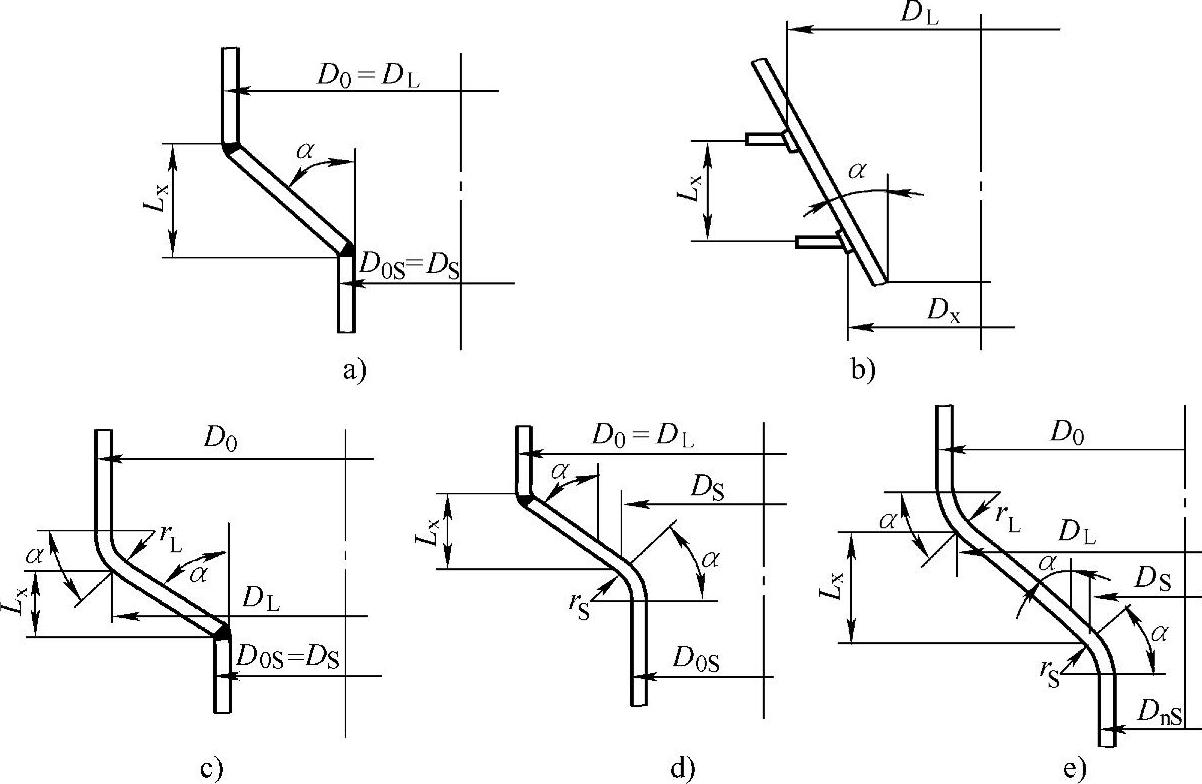
图4-15 锥壳的相关计算尺寸

a）无折边锥壳 b）锥壳上相邻两加强圈之间锥壳段c）大端折边锥壳 d）小端折边锥壳 e）折边锥壳

半锥角α≤60°的外压锥形封头的计算过程如下：

1）假设壁厚t_n，计算t_e=t_n-C。

2）计算：

①等效圆筒壁厚t_ε。

②等效圆筒长度L_ε。

③等效圆筒外径D₀=D_L。

3）由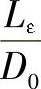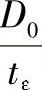，查图4-7（以Lε代替L，tε代替δ_e）得到A。

4）按所用材料，查外压应力系数选用表4-1确定对应的外压应力系数B曲线图，再按对应的外压应力系数B曲线图4-8～图4-12，由A值向上引垂线，查B值。

5）由公式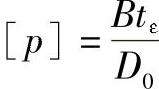，得到许用外压[p]。

6）比较计算外压p_c和许用外压[p]，要求p_c≤[p]且较接近。

（2）半锥角α＞60°的外压锥形封头

半锥角α＞60°的外压锥形封头按平板封头计算，圆平板直径取锥壳最大直径。