外压应力系数B曲线用于外压圆筒计算原理

从外压容器的失稳分析可知，对于设计计算来说外压圆筒的壁厚是一个未知量，所以需要一个反复试算的过程。显然用解析法进行外压容器的计算比较繁杂，因此GB150.1～150.4—2011推荐使用比较简便的图算法。

1.图算法的原理

外压圆筒按照圆筒的长度可以分成以下3类：

（1）长圆筒（L＞L_cr）

1）这类圆筒有以下特征：临界压力p_cr与材料的E和μ、壁厚t_e、直径D₀有关，和长度L无关。

2）临界压力p_cr的计算公式：任意材料圆筒用式（4-3），钢制圆筒用式（4-4）。

3）失稳波数n=2。

（2）短圆筒（L≤L_cr）

1）临界压力p_cr与材料的E和μ、D₀/t_e、L/D₀有关。

2）临界压力p_cr的计算公式：任意材料圆筒用式（4-6），钢制圆筒用式（4-9）。

3）失稳波数n＞2。

（3）刚性圆筒

失效是由于器壁中的压应力达到材料的屈服极限而引起的塑性屈服破坏，因此不存在稳定性问题，只需校核强度是否足够，L的影响不计。

假定材料的应力-应变曲线为理想弹塑性模型，则对不同的t/D₀值可在双对数坐标纸上标绘强度和失稳失效曲线，如图4-6所示。这种曲线由三部分组成，分别代表了上述三种圆筒的力学特征。

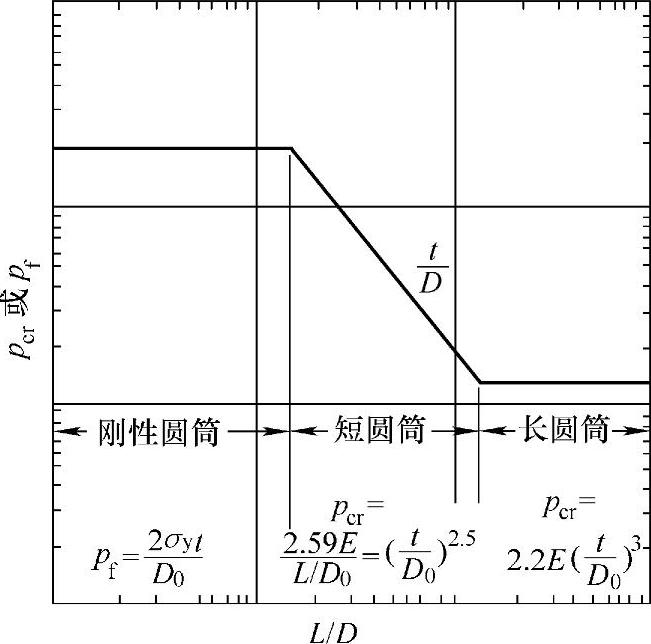
图4-6 外压圆筒的失效曲线

这种曲线还可以用另一种标绘法，由式（4-5）和式（4-10）知：

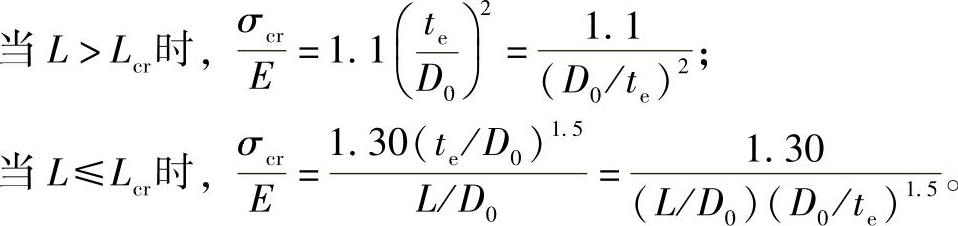
从以上两个公式可以看出：等式左侧为材料性能参数，等式右侧为几何尺寸参数。因为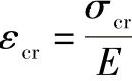，令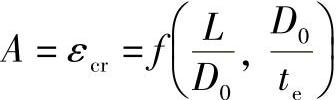，若以A=ε_cr为横坐标，以L/D₀为纵坐标，可以得到不同（D₀/t_e）比值的一簇曲线，如图4-7所示。

若已知L、D₀、t_e，在图4-7中就可查得A值。因为A代表临界应力所对应的周向应变，即

而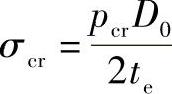，则得

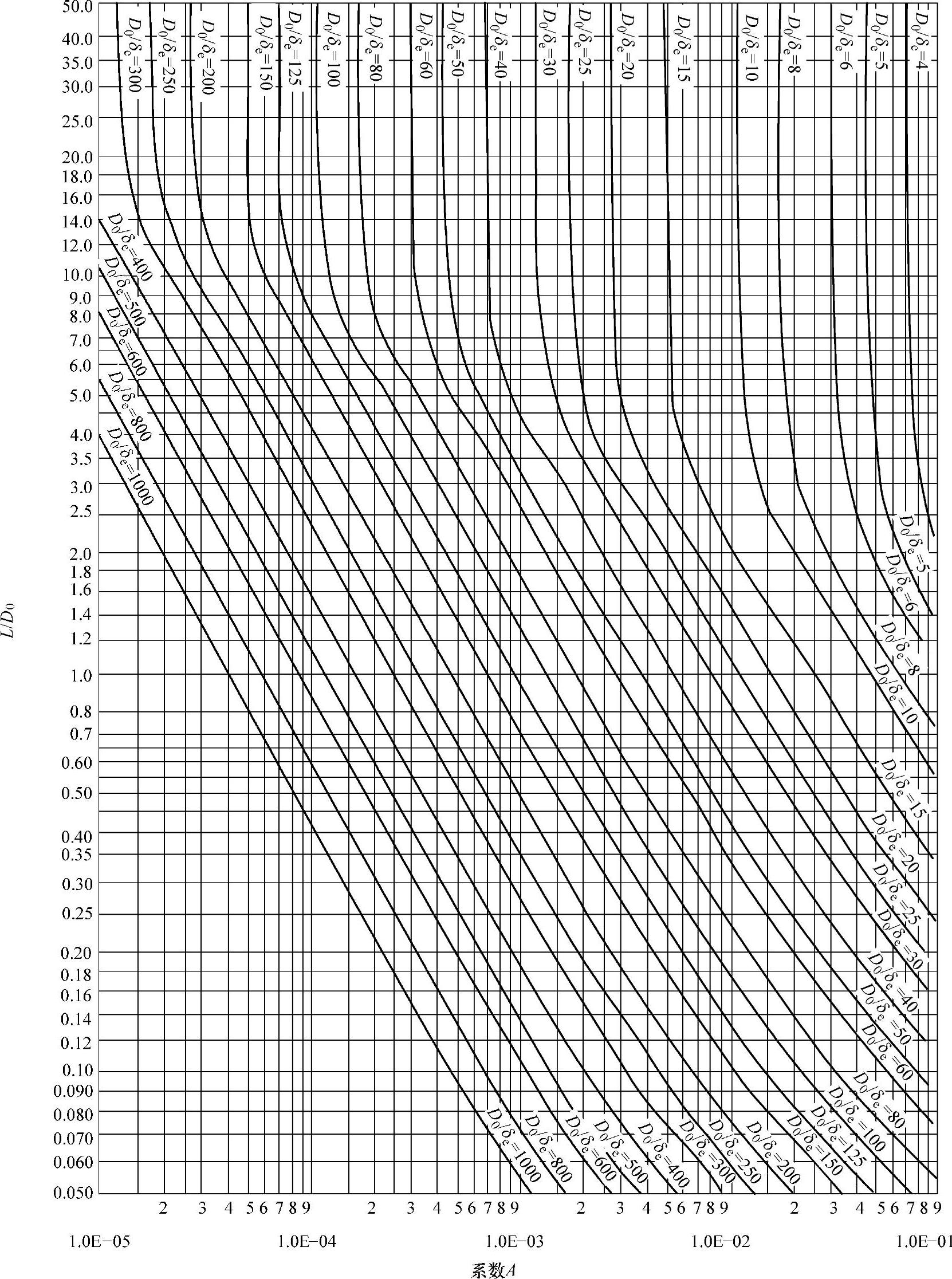
图4-7 外压应变系数A曲线

我国稳定系数m=3，将m=3代入式（4-14）中，得

令

将式（4-15）代入式（4-16）中，得

因为A=ε_cr，所以B与A的关系就是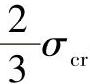与ε_cr的关系。利用材料单向拉伸的应力-应变关系（对于钢材应力-应变曲线与压缩曲线大致相同），将纵坐标乘以2/3，即可作出B与A的曲线，如图4-8～图4-14所示（因为同种材料在不同温度下的应力-应变曲线不同，所以图中考虑了一组不同温度的曲线，或称材料温度线）。在GB150.1～150.4—2011中绘制了更多材料的厚度计算图，在这里只摘取了其中常用的7张图，如有需要可查GB150.1～150.4—2011获取。

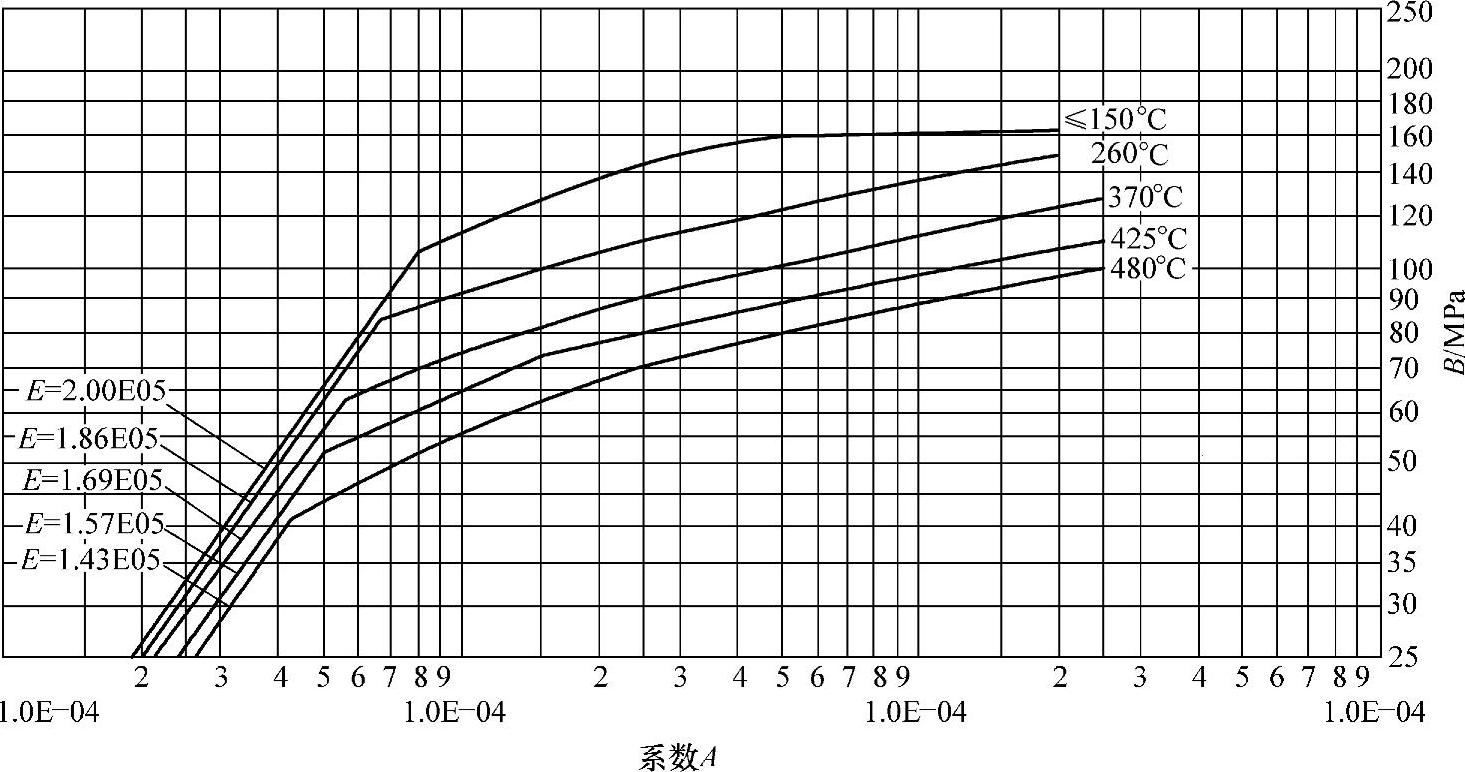
图4-8 外压应力系数B曲线（除Q345R外的R_eL>207MPa的碳钢、低合金钢和S11306钢等）

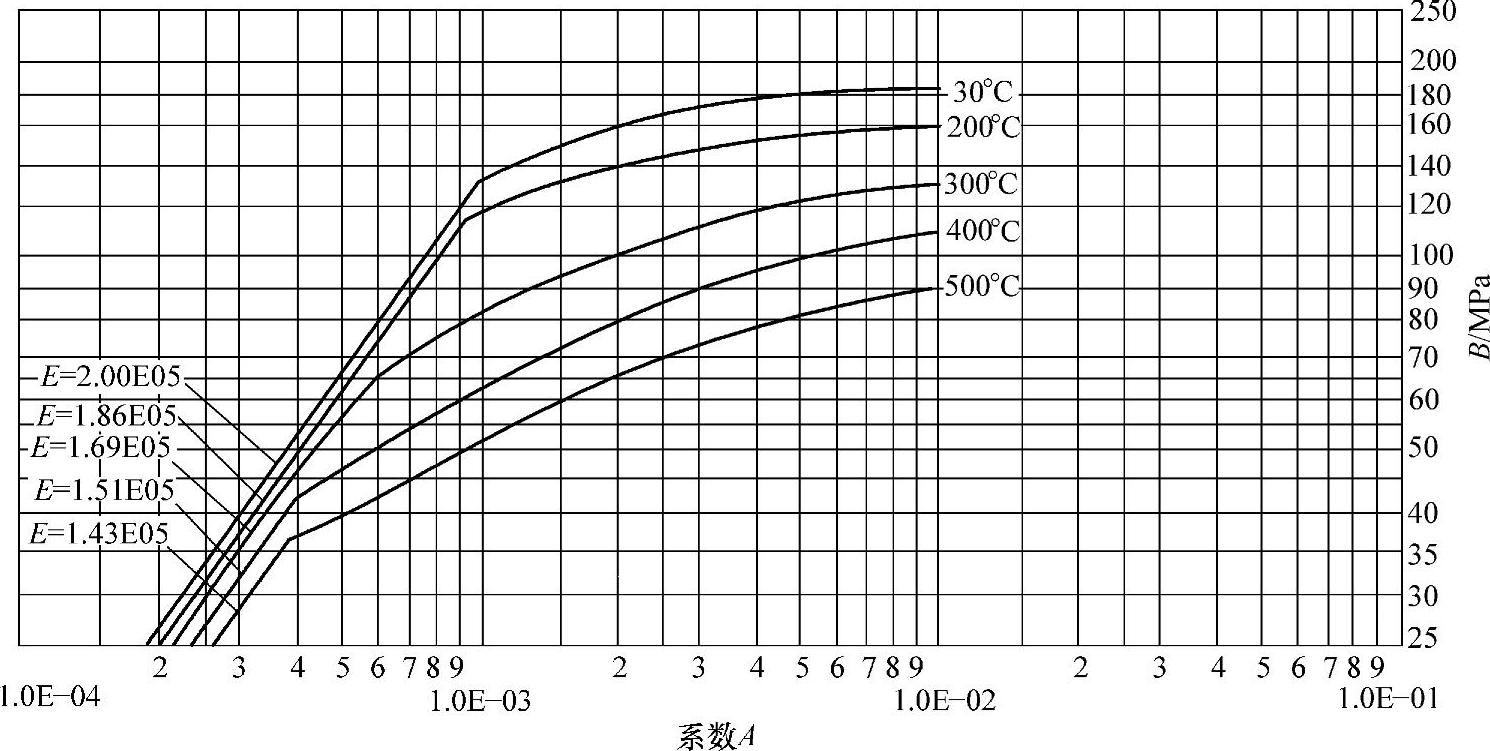
图4-9 外压应力系数B曲线（Q345R材料）

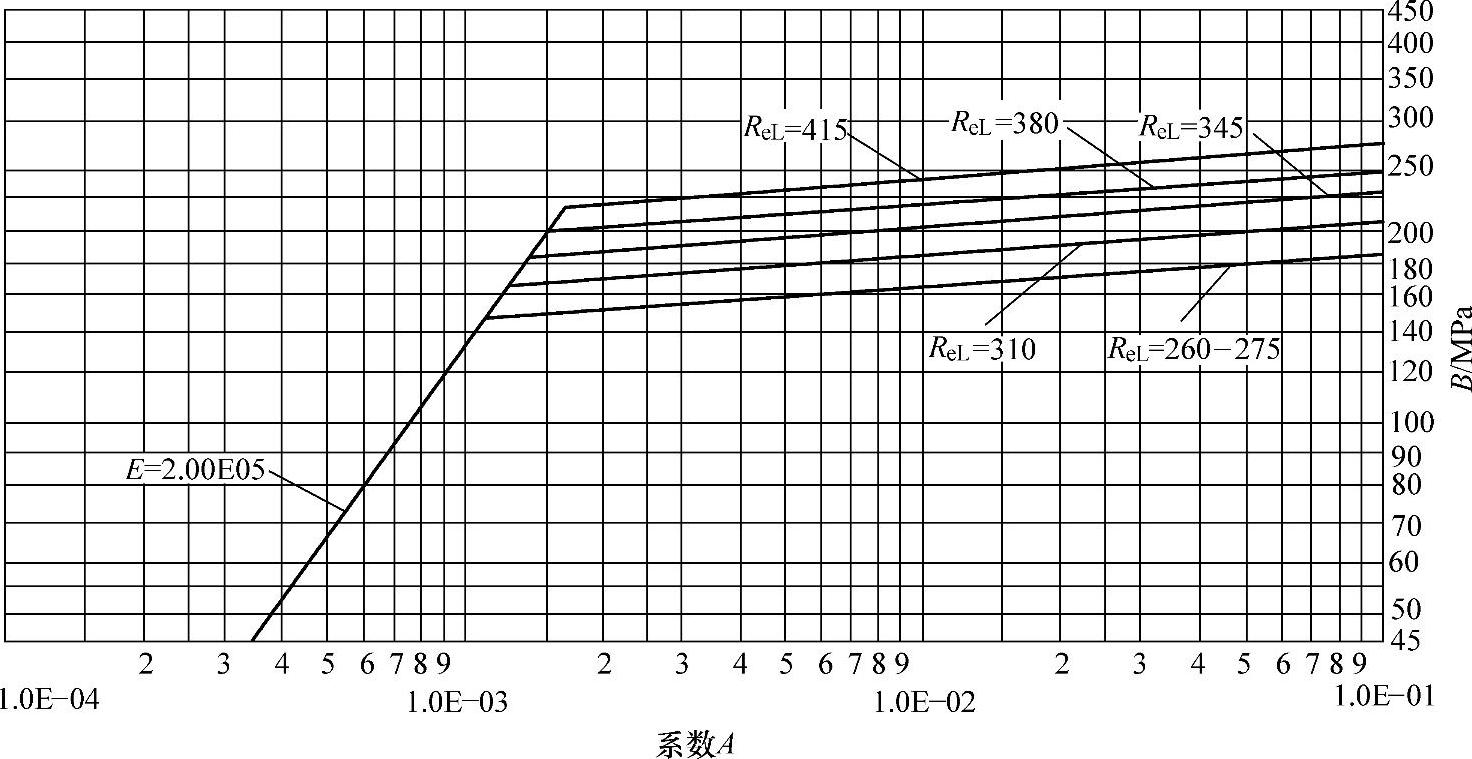
图4-10 外压应力系数B曲线（除Q345R外的R_eL>260MPa的碳钢、低合金钢等）

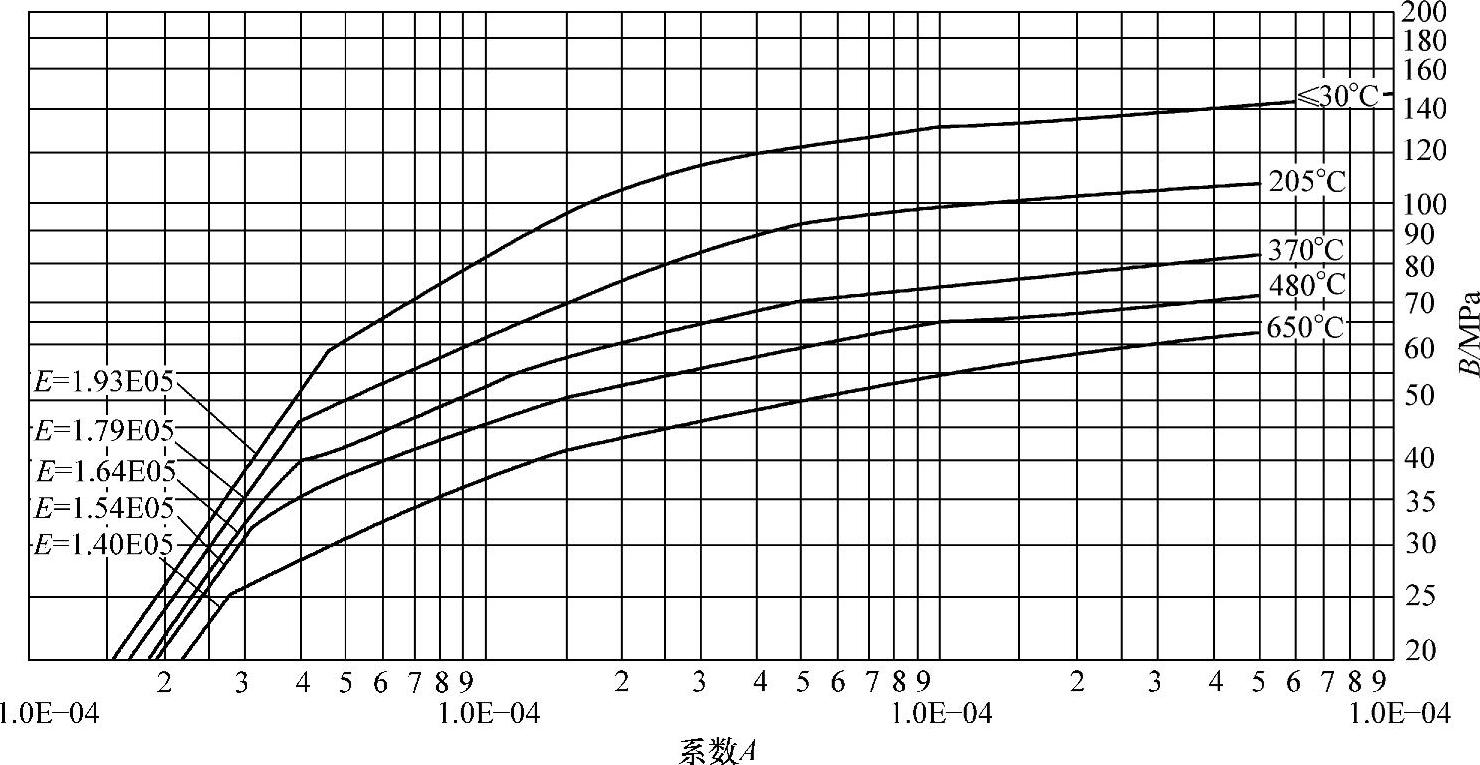
图4-11 外压应力系数B曲线（S30408钢等）

(www.xing528.com)

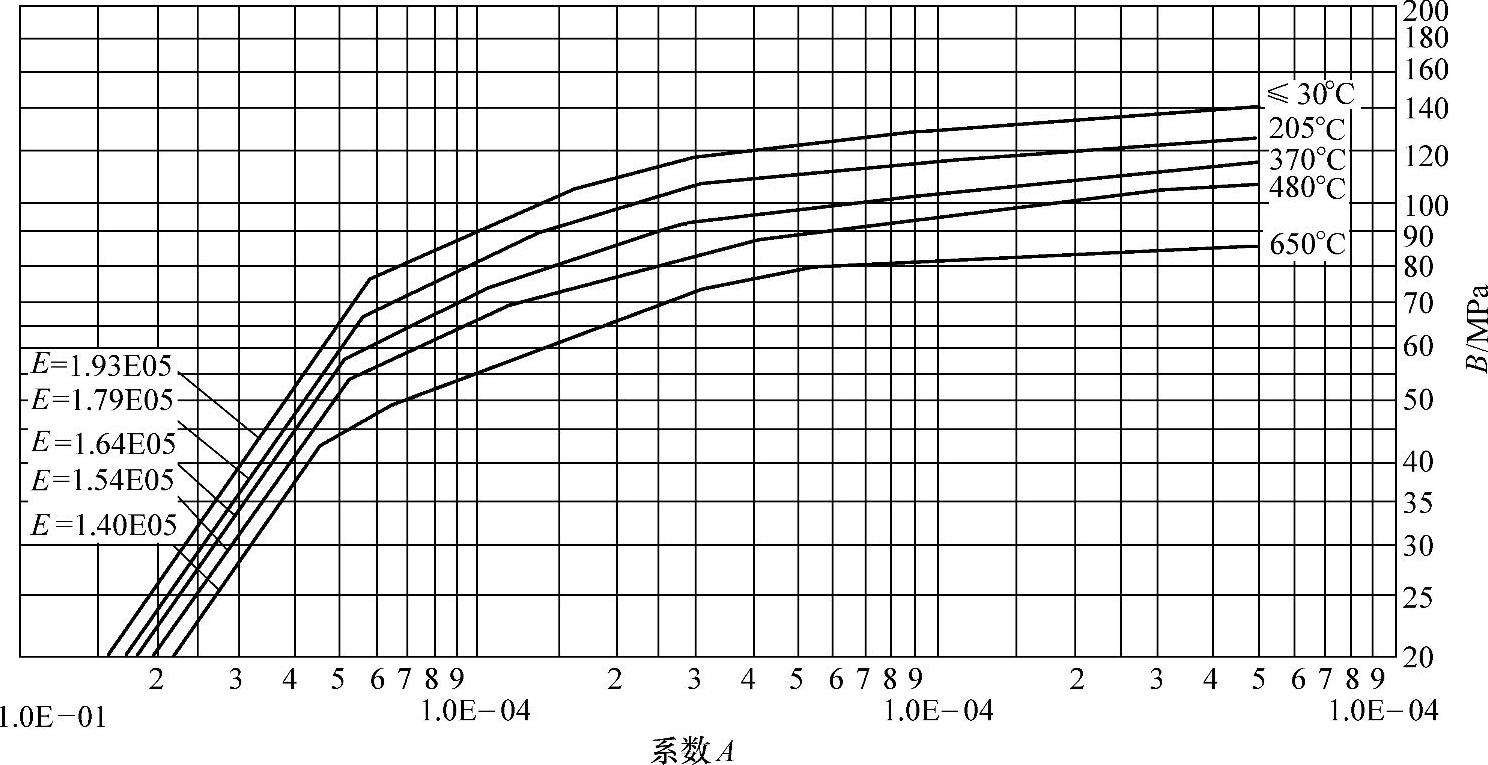
图4-12 外压应力系数B曲线（S31608钢等）

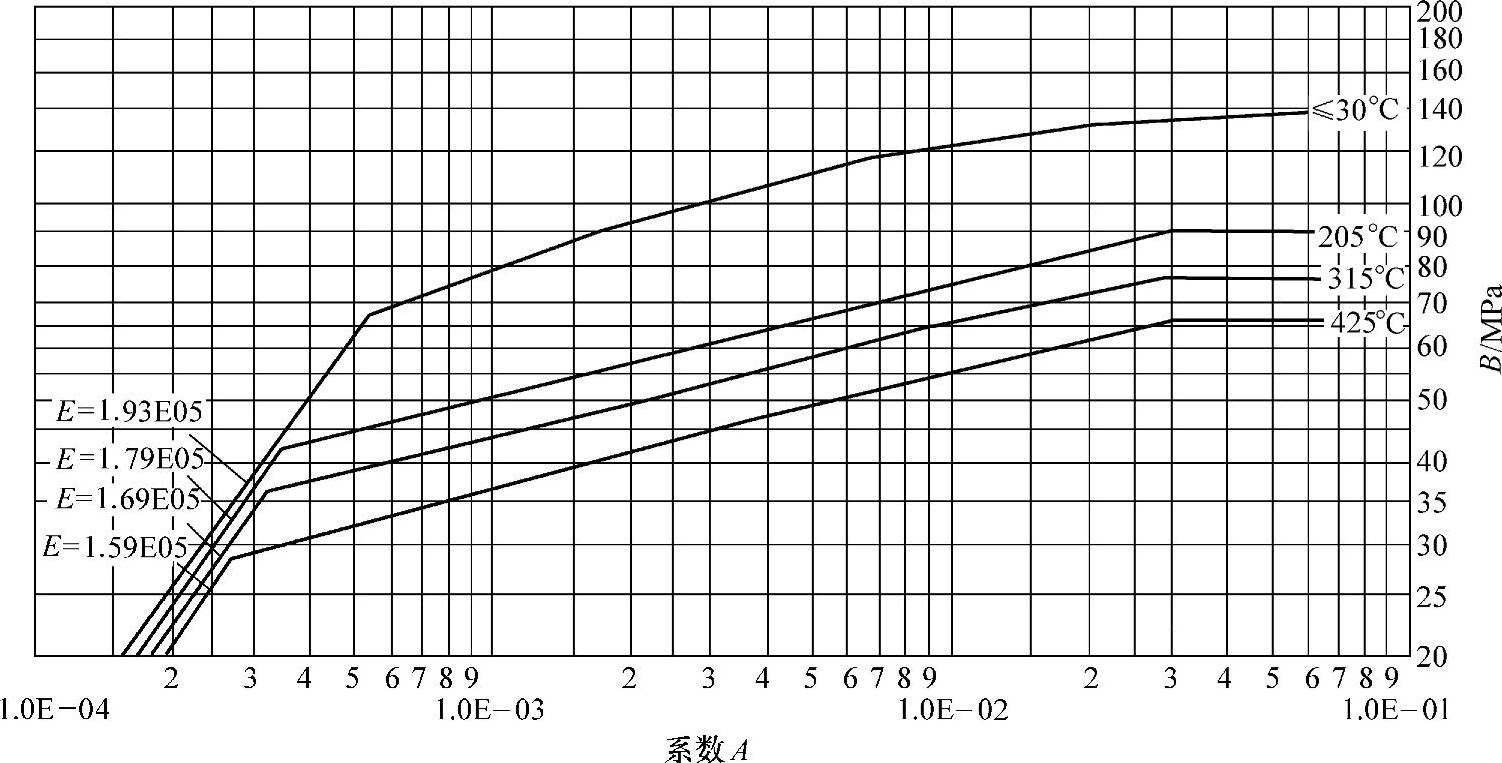
图4-13 外压应力系数B曲线（S30403钢等）

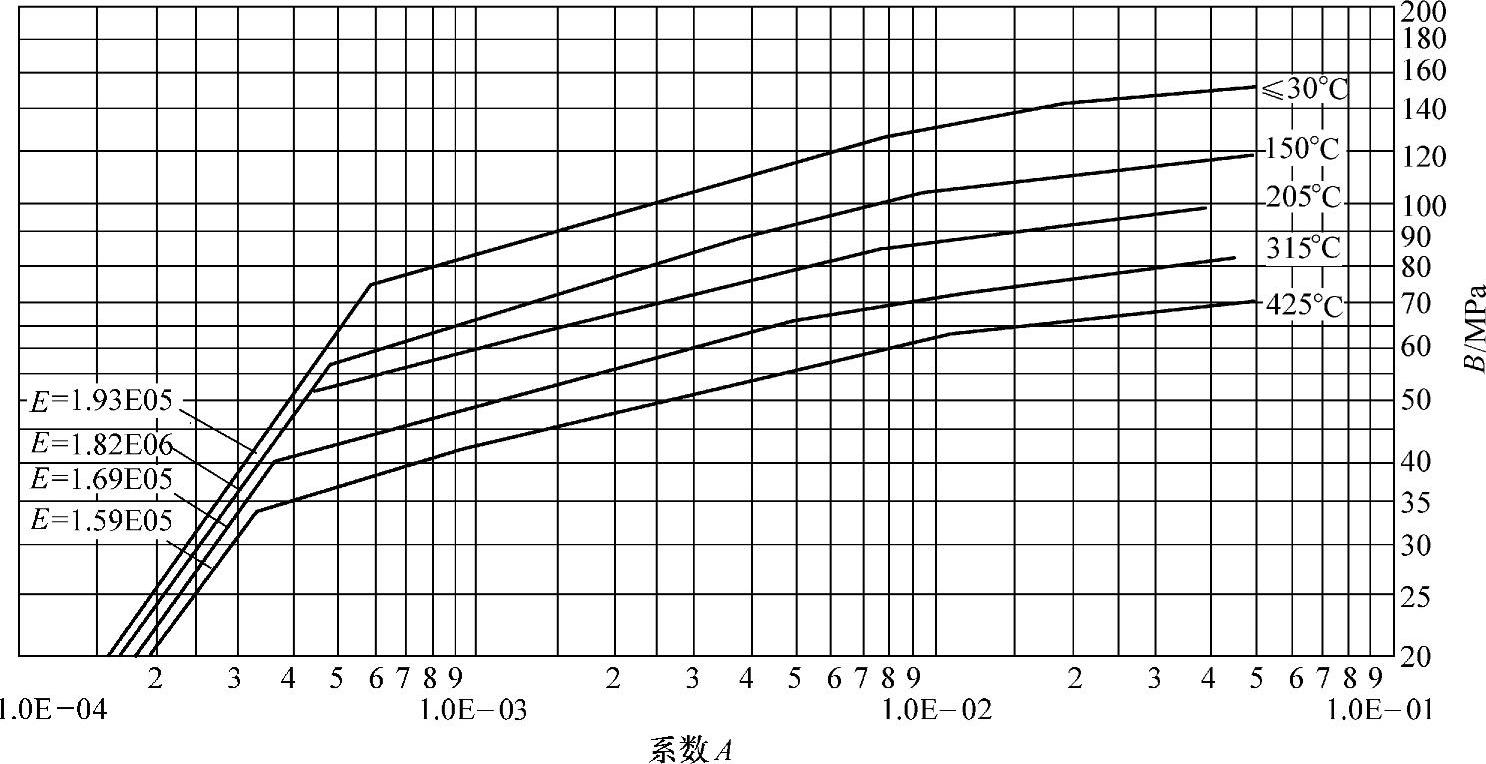
图4-14 外压应力系数B曲线（S31603钢等）

图4-8～图4-14与图4-7有共同的横坐标A，因此由图4-7中查得A值后，再在图4-8～图4-14中查得相应设计温度下的B值，继而由式（4-16）计算出[p]，这就是利用图算法计算外压圆筒的基本原理。

计算时还应注意以下几点：

1）图4-8～图4-14中左下方直线大部分被省略掉了，因为在弹性范围内许用外压力可直接由A值通过式（4-15）直接计算出。

2）若查图4-8～图4-14时，A值超出设计温度下曲线的最大值，则取对应温度下曲线的右端点的纵坐标值为B值。

3）在塑性范围内，因为使用正切弹性模量，即曲线上任一点的斜率为E_t=dσ/dε，所以上述图算法对非弹性失稳也同样适用。

4）由图4-7（以t_e代替δ_e）可知，D₀/t_e＜10的圆筒，其A=ε_cr>1%（ε_cr=σ_cr/E＞10^-2，则σ_cr＞E×10^-2，得σ_cr＞10⁵×10^-2=10³），此时σ_cr已超过了材料的屈服极限R_eL，则圆筒可能发生塑性失稳或塑性屈服破坏，所以要求从稳定性和强度两方面来考虑，即许用设计外压取下列两个压力的较小值。

①由强度导出：

②由稳定性导出：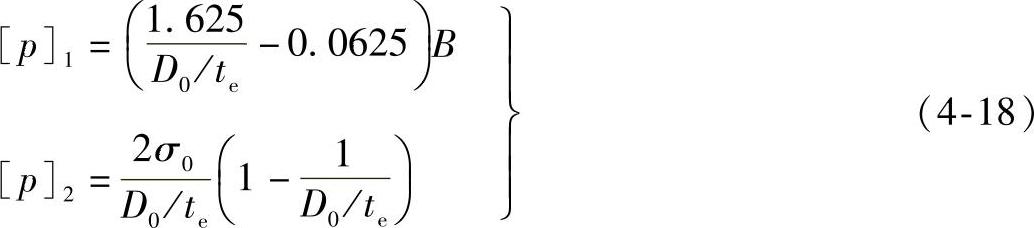

其中σ₀取2[σ]^t和0.9R^t_eL的较小值。

5）对于D₀/t_e＜4的外压圆筒，无论长或短圆筒，其A=ε_cr＞6.875%，已进入屈服，故B值都一样，因而可以按长圆筒式（4-5）计算A值，即

6）当A>0.1时，已超出图算范围，均按A=0.1计算。

2.图算法的计算步骤

在图算法中，都以有效厚度t_e=t_n-C代替式中t。计算分以下三种情况：

1）以D₀/t_e≥10为例说明一般的计算步骤。

①假设壁厚t_n，计算筒体长度L和t_e。

②计算L/D₀、D₀/t_e。

③在图4-7中查A（遇中间值用内插法），若L/D₀值大于50，则用L/D₀=50查A；若L/D₀值小于0.05，则用L/D₀=0.05查A。

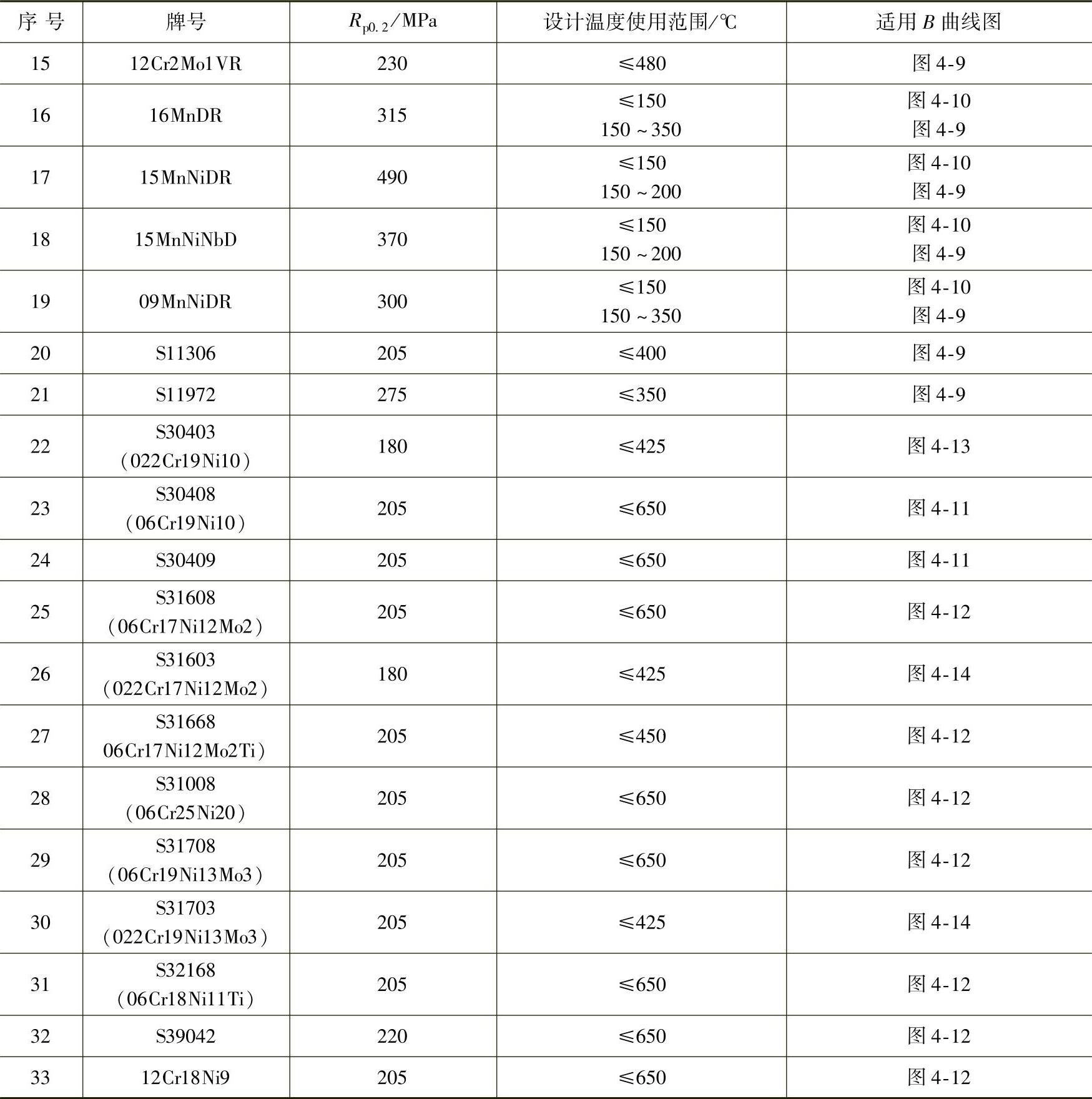
④按所用材料，查外压应力系数选用表4-1确定对应的外压应力系数B曲线图，再按对应的外压应力系数B曲线图4-8～图4-14，由A值向上引垂线，查B值。

表4-1 外压应力系数B曲线图选用表

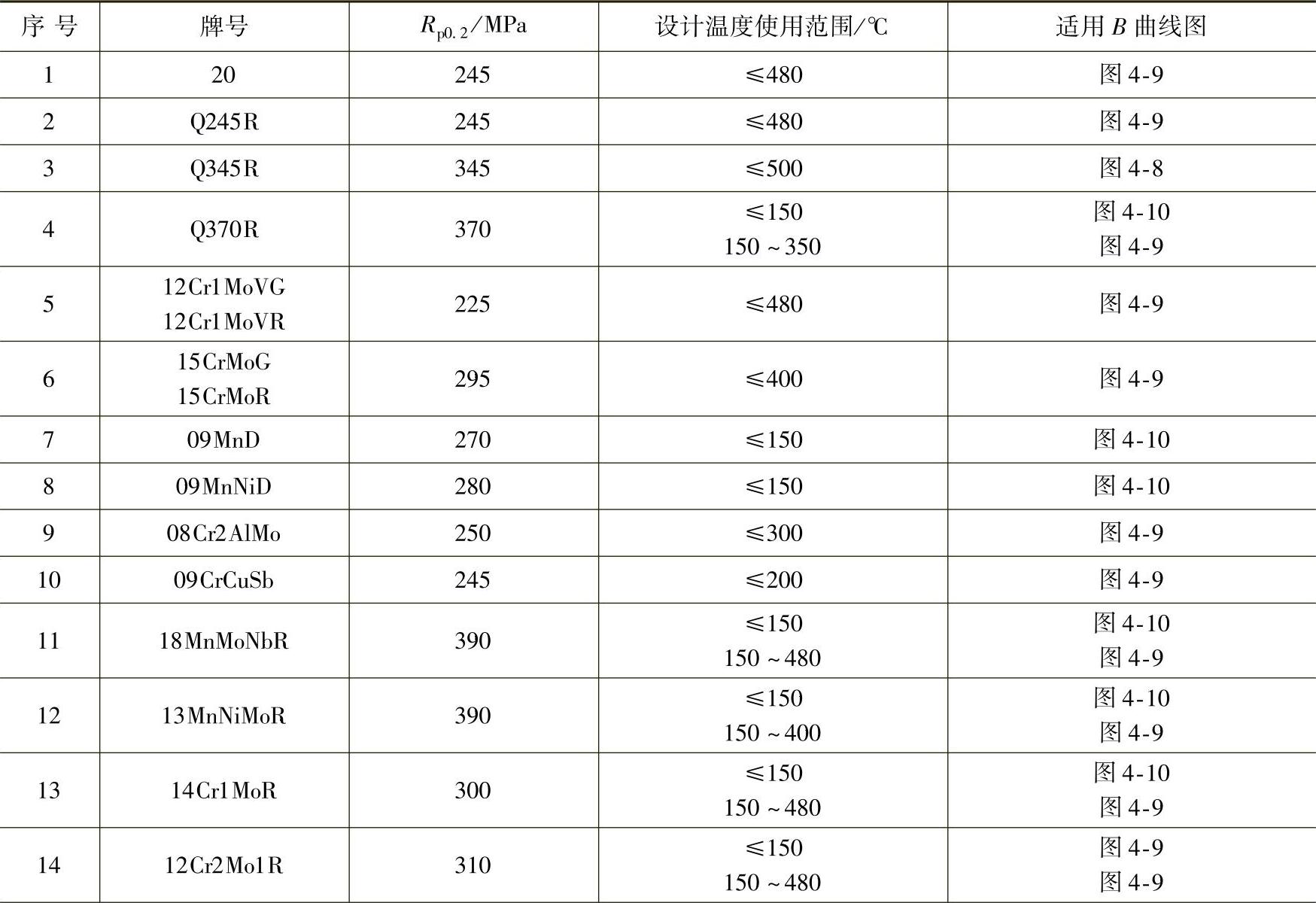
（续）

若A在设计温度的材料线右方，则垂直移动与材料温度线相交（遇中间温度用内插法），再水平右移，在图的右方纵坐标上得到B值，并按下式计算许用设计外压[p]：

若A值在材料温度线左方，说明发生的是弹性失稳，可按下式计算许用设计外压[p]：

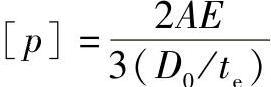
⑤比较p_c和[p]，若p_c≤[p]且较接近，则假设的t_n符合要求。

2）若D₀/t_e＜10的圆筒，其A=ε_cr＞1%，此时σ_cr已超过R_eL，圆筒可能发生塑性失稳或塑性屈服破坏，所以要求按稳定性和强度两方面来考虑。

①同上步骤求出B值。

②按式（4-18）计算[p]₁和[p]₂，最终取较小值作为许用设计外压[p]。

3）若D₀/t_e<4的圆筒，无论长、短圆筒，其A=ε_cr>6.875%，已进入屈服，故B值都一样。

①按照长圆筒的式（4-19）计算A；当A>0.1时，已超出图算的范围，均按A=0.1计算。

②按照式（4-17）计算B值。

③按式（4-18）计算[p]₁和[p]₂，取较小值作为许用设计外压[p]。