如何计算临界压力？

外压圆筒按其相对长度可分为以下3类：

（1）长圆筒：当圆筒的长度与直径之比较大时，其中间部分将不受两端封头或加强圈的支持作用，弹性失稳时形成n=2的波数，这种圆筒称为长圆筒。长圆筒的临界压力与长度无关，仅与圆筒的壁厚与直径的比值有关。

（2）短圆筒：当圆筒的长度与直径之比较小时，两端的约束作用不能忽视。临界压力不仅和圆筒的壁厚与直径的比值有关，而且和长度与直径的比值有关，失稳波数大于2，这种圆筒称为短圆筒。

（3）刚性圆筒：圆筒的长度与直径之比较小，而壁厚与直径比很大，即圆筒刚性很大，此时圆筒的失效形式已不是失稳，而是压缩强度破坏，这种圆筒称为刚性圆筒。

这里我们主要讨论长圆筒和短圆筒的临界压力。

1.受均布侧向外压长圆筒的临界压力

对于长圆筒来说，它的失稳不受圆筒两端的约束作用，因此我们可以从远离筒体端部处取一单位长度的圆环，用圆环的临界压力计算代替长圆筒的临界压力计算，只是要求在计算中采用不同的轴向抗弯刚度。

（1）圆环的临界压力

用静力平衡法求解圆环的临界载荷时，首先假设：当圆环的径向均布压缩载荷q达到某一值时，其原横截面的圆形形状处于不稳定状态，发生了微小的弹性弯曲变形，变成近似椭圆形状，如图4-3所示。于是可以列出在这种弯曲变形状态下的力平衡微分方程组，然后求出线性微分方程式，最后求出圆环失去稳定的最小临界压力（详细推导过程可查相关文献）。

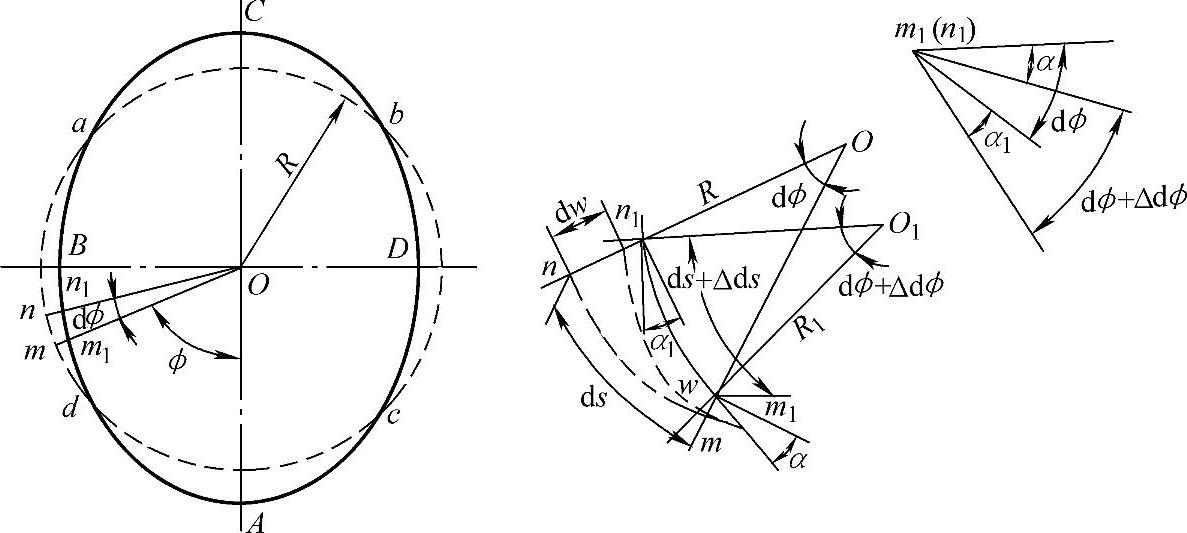
图4-3 圆环变形的几何关系

圆环的挠度曲线微分方程：

式中 M——弯矩；

EJ——圆环的抗弯刚度；

R——圆环半径；

w——变形前后m点的径向位移；

ds——变形前圆环上切出任意弧的弧长。

圆环受力与变形的关系如图4-4所示。

圆环临界压力计算表达式（圆环截面惯性矩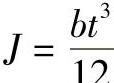，取b=1，其中b为圆环的单位厚度）：

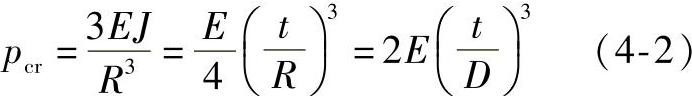
图4-4 圆环受力与变形的关系

式中 p_cr——沿圆环单位周长上的载荷；

t——圆环的壁厚；

R——圆环中性面的半径，D=2R；

E——圆环材料的弹性模量。

（2）长圆筒的临界压力

对于仅受周向均布外压的长圆筒来说，由于圆筒的抗弯刚度大于圆环，故在式（4-2）中用圆筒的抗弯刚度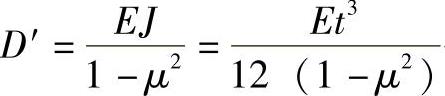代替EJ，得

式中 D——圆筒的中面直径（一般取圆筒外径D₀≈D）；

t——圆筒的厚度（不包括厚度附加量）。

式（4-3）即为长圆筒受周向均布外压失稳的临界压力计算式，此式在1866年首先由Bresse导出。

对于钢制圆筒，可取_μ=0.3，并以D₀代替D，t_e代替t，则式（4-3）改写为(www.xing528.com)

式中 D₀——圆筒的外径；

t_e——圆筒的有效厚度。

临界应力在圆筒器壁中引起的周向压缩应力，称为临界应力。临界应力可用式（4-5）来表示：

式（4-5）即为长圆筒受周向均布外压失稳的临界应力计算式。

要注意的是，式（4-4）仅适用于弹性范围，即临界应力σ_cr小于材料的比例极限σ^t_p，一般取σ^t_p≈R_eL。当临界应力σ_cr超过材料的比例极限σ^t_p时，应力与应变不再呈线性关系，筒体将发生非弹性失稳或塑性屈服失效。

2.受均布侧向外压短圆筒的临界压力

对于短圆筒来说，它两端的约束或刚性构件对筒体的变形支承作用较为显著，因此它失稳时会出现两个以上的波数，它的临界压力的计算比较复杂。短圆筒的临界压力公式是米赛斯（Mi_- ses）首先在1914年按线性小挠度理论导出的。

米赛斯（Mises）公式：

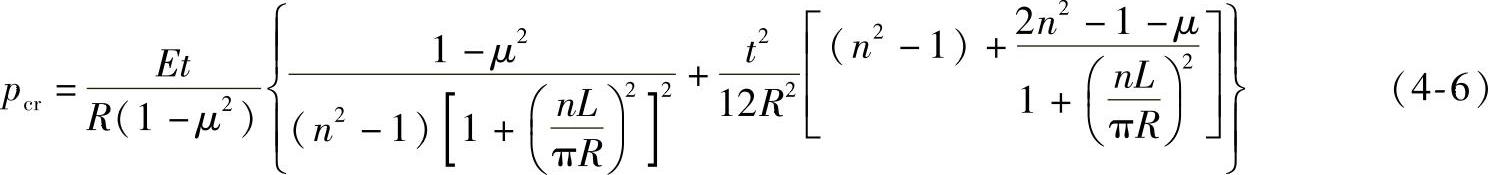
式中 p_cr——短圆筒临界压力；

L——圆筒的计算长度；

t——圆筒的壁厚；

R——圆筒中间面的半径；

n——圆筒失稳时的波数；

E——圆筒材料的弹性模量；

μ——圆筒材料的泊松比。

从式（4-6）可以看出，如果筒体的几何尺寸和材料为定值，则不同的波数n会对应不同的临界压力p_cr，且p_cr不随n的增大而单调增大，p_cr会有一个极小值，而p_cr的极小值才是筒体真正的临界压力。

用微分法计算p_cr的极小值十分复杂，常用试算法求解。为简化计算，在工程中常用近似方法。认为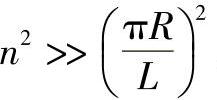，故式（4-6）中的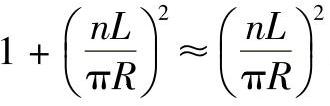，并略去方括号中第二项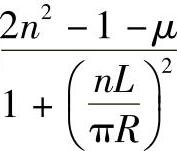，得

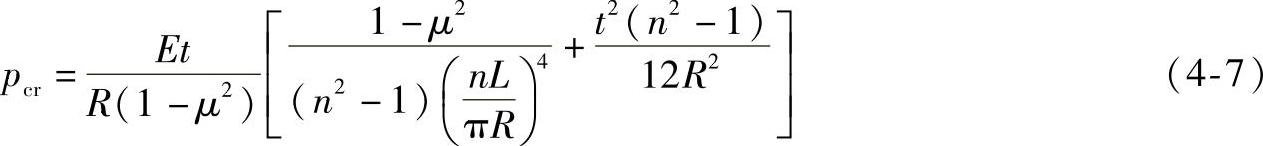
式（4-7）是由R.V.Southwell首先推出的短圆筒临界压力计算简化式。

要求p_cr极小值时的波数，令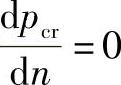，并取n²-1≈n²，μ=0.3，可得与最小临界压力相应的波数：

将式（4-8）代入式（4-7）中，考虑到短圆筒n值较大，所以仍取n²-1≈n²，μ=0.3，D=D₀，即得短圆筒最小临界压力的近似计算式：

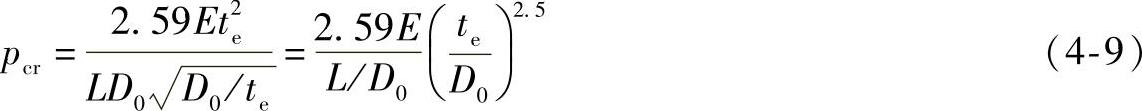
式（4-9）亦称拉姆（B.M.Pamm）近似式，它的计算结果比米赛斯（Mises）公式低12%，故偏于安全。

临界压力下，短圆筒的周向压缩应力称为临界应力，可表示为

式（4-9）仅适用于弹性失稳，即σ_cr<σ^t_p的场合。

3.临界长度

对于给定D和t的圆筒，有一特征长度作为区分长圆筒和短圆筒的界限，此特性尺寸称为临界长度，以L_cr表示。当圆筒的计算长度L>L_cr时，属于长圆筒；当圆筒的计算长度L<L_cr时，属于短圆筒；当L=L_cr时，则按长、短圆筒求得的临界压力应相等，即