圆板均布载荷下的应力和变形分析

如果圆板上作用的为横向均布载荷，p_z=p，则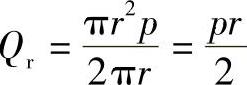，将弯曲微分方程式（3-29）

对r连续两次积分，得到挠曲面法向转角：

对上式再次积分，得到中面在弯曲后的挠度：

式中C₁、C₂、C₃均为积分常数。

对于圆平板，在板中心处（r=0）挠曲面转角与挠度均为有限值，因而要求积分常数C₂=0，C₁、C₃由边界条件确定。工程中，有两种典型支承情况（两种边界条件）：周边固支圆平板和周边简支圆平板，如图3-21所示。

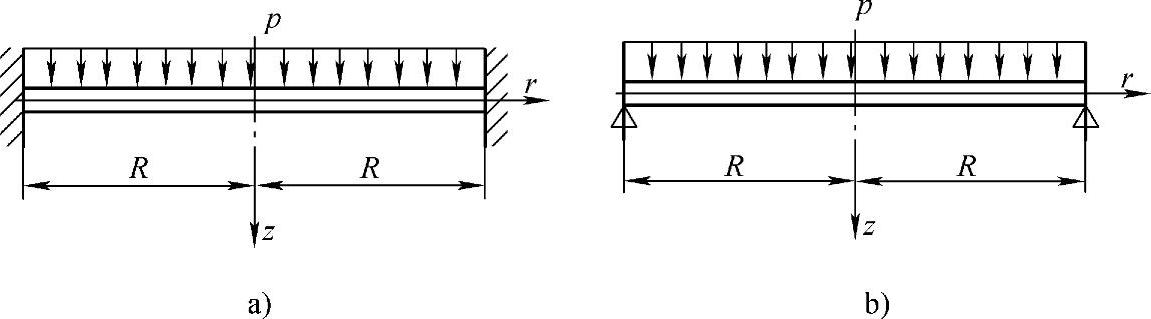
图3-21 不同周边支承条件下的圆平板

1.周边固支圆平板（图3-21a）

在支承处不允许有挠度和转角，即

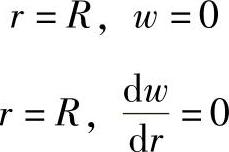
将上述边界条件代入式（3-30）和式（3-31），解得积分常数：

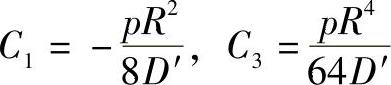
得到转角和挠度表达式：

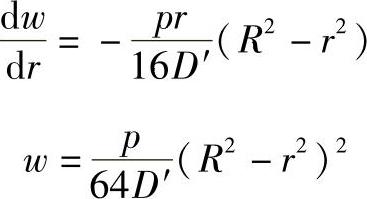
将上式带入弯矩表达式（3-27），得固支条件下的周边固支圆平板弯矩：

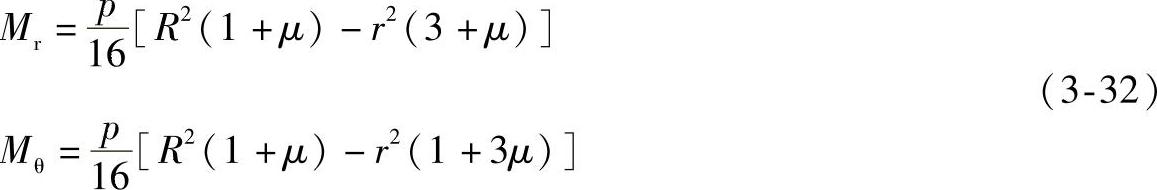
代入弯曲应力计算式（3-28b），可得任意半径r处上、下板面的应力表达式：

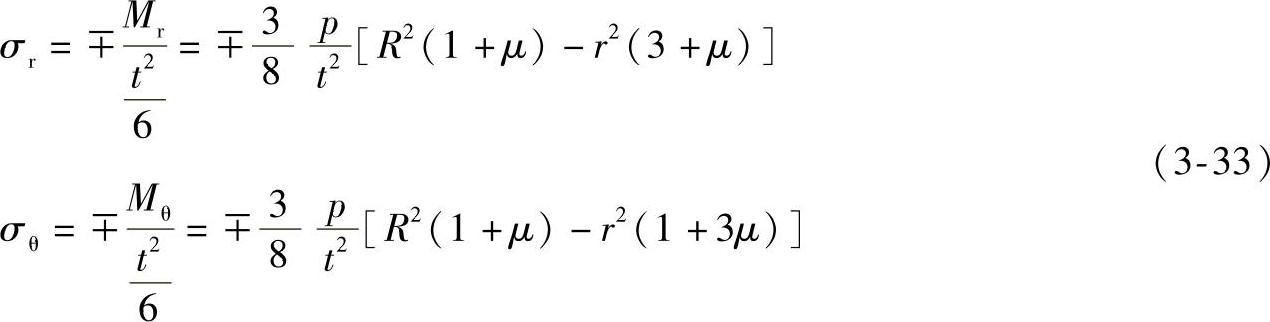
均布载荷下，周边固支圆平板下表面的应力分布，如图3-22a所示。最大应力在板边缘上下表面，即

(www.xing528.com)

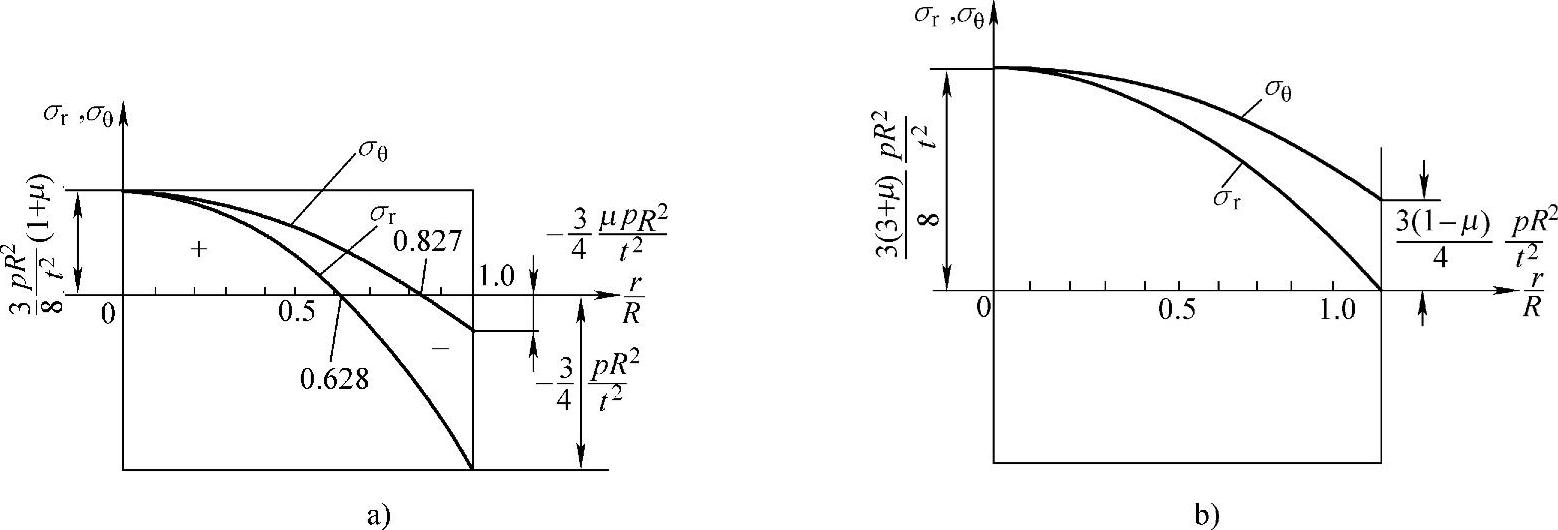
图3-22 均布载荷圆平板的弯曲应力分布（板下表面）

a）周边固支 b）周边简支

2.周边简支圆平板（图3-22b）

r=R，w=0

r=R，M_r=0

同理可推得弯矩表达式为

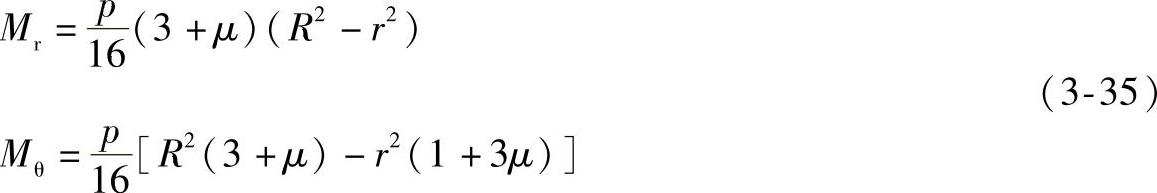
应力表达式为

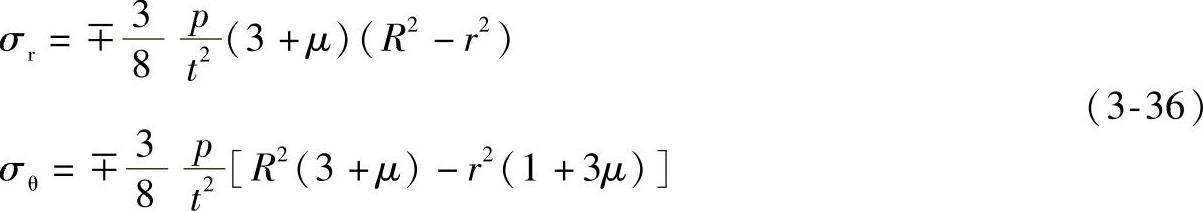
最大弯矩和相应的最大应力均在板中心r=0处：

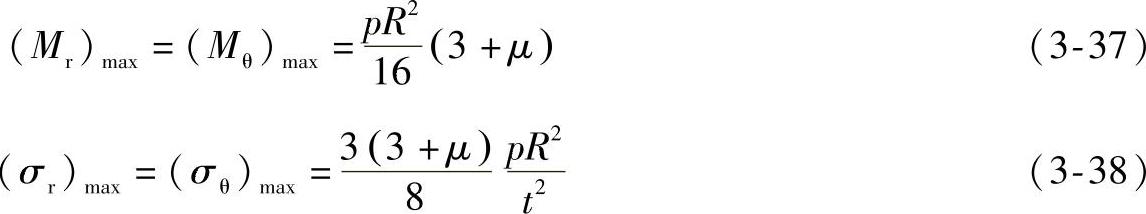
3.支承对平板刚度和强度的影响比较

周边简支时，最大挠度在板中心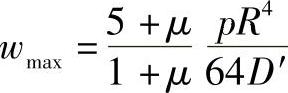

周边固支时，最大挠度在板中心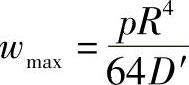

对于钢材μ=0.3，周边简支板的最大挠度约为周边固支板的最大挠度的4.08倍。

周边固支圆平板中的最大正应力为支承处的径向应力，其值为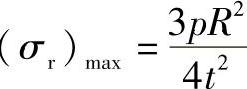，周边简支圆平板中的最大正应力为板中心处的径向应力，其值为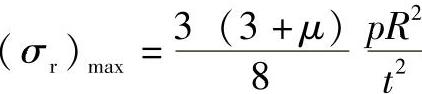。对于钢材μ=0.3，周边简支板的最大正应力约为周边固支板的最大正应力的1.65倍。

可见，周边固支的圆平板在刚度和强度两方面均优于周边简支圆平板。实际工程中，平板的周边支承结构介于周边固支和周边简支之间。

通常最大挠度和最大应力与圆平板的材料（E、μ）、半径、厚度有关。因此，若构成板的材料和载荷已确定，则减小半径或增加厚度都可减小挠度和降低最大正应力。当圆平板的几何尺寸和载荷一定时，则选用E、μ较大的材料，可以减小最大挠度。然而实际上由于钢材的E、μ变化较小，故采用此法并不合理。较多的是采用改变其周边支承结构，使它更趋近于固支条件；增加圆平板厚度或用正交栅格、圆环肋加固平板等方法来提高圆平板的强度与刚度。

薄板结构正应力σ_r、σ_θ沿板厚度呈直线分布，在板的上下表面有最大值，是纯弯曲应力。最大弯曲应力σ_max与（R/t）2成正比，而回转薄壁壳体的薄膜应力与R/t成正比，故在相同R/t条件下，薄板所需厚度比薄壁壳体大。