如果将回转薄壁壳体看成气球，当气球被吹胀时，其经线方向和周向（平行圆）方向的长度都将增大。受内压的薄壁容器与气球受力类似。作用在薄壁壳体的压力将使壳体经线被拉长，经线方向可能断裂，即在垂直经线的断面分布有应力，其作用方向是沿着容器的经线的切向，称为“经向应力”，用σϕ表示。同时，该压力将使薄壁壳体周向线破裂，这种沿圆周的切线方向产生的应力，称为“周向应力”或“环向应为”，用σθ表示（见图3-2和图3-3a）。受内压作用时，经向应力和周向应力为拉应力，而受外压作用时，这两项应力为压应力。
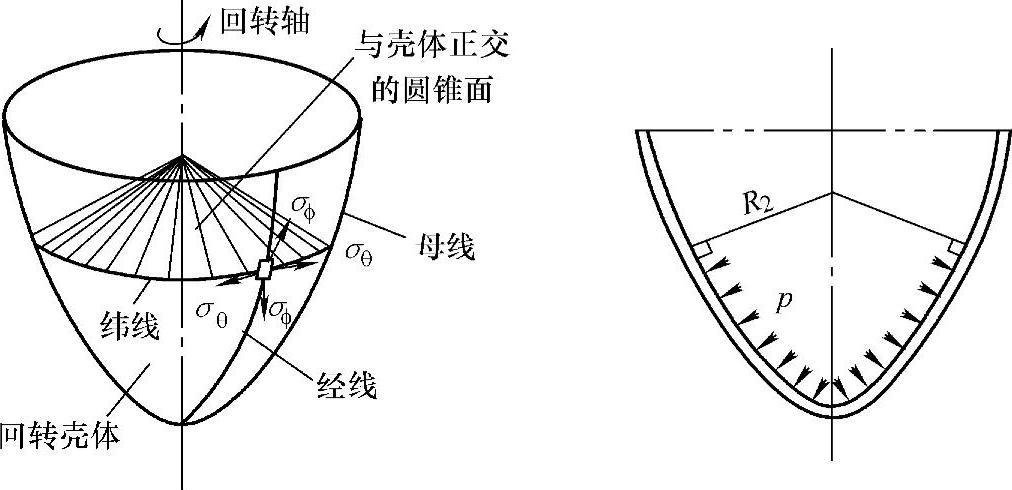
图3-2 回转壳体上的薄膜应力
介质压力作用在壳体壁上，还引起壳体厚度方向各层材料的挤压，由此产生沿半径方向的径向应力，用σr表示。径向应力为压应力。
此外，薄壁容器在介质压力作用下，除经线长度变化外，经线的曲率也将发生变化，这意味着经线方向还作用有弯矩和剪力。同样，圆周方向也作用有弯矩和剪力。由此产生弯曲应力和剪应力（见图3-3b、c）。由于这里研究的是轴对称问题，图3-3中剪力Nϕθ=Nϕθ=0，Qθ=0，扭矩Mϕθ=0，Mϕθ=0。
分析求解回转薄壁壳体中的应力值可以用两种理论，即无力矩理论和有力矩理论。
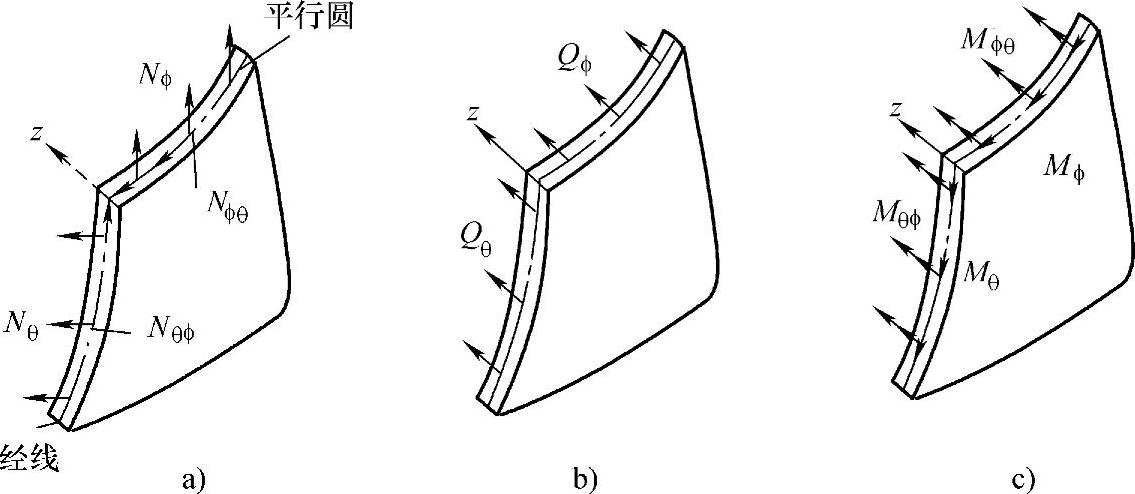
图3-3 一般壳体上的内力
无力矩理论又称为薄膜理论。它假定壁厚t与直径相比很小，认为壁厚很薄，几乎像薄膜那样，抗弯刚度非常小，或者中面的曲率改变非常小，弯矩产生的弯曲应力很小。故薄壁壳体只承受经向应力σϕ和周向应力σθ，不承受弯矩和剪力，且认为壳体内的经向应力和周向应力沿厚度是均匀分布的。在壳体很薄时，沿厚度方向的应力σr与上述两相应力相比很小而忽略。这种分析理论中，器壁的应力称为“薄膜应力”。
在壳体理论中，若同时考虑薄膜应力和弯曲、剪切应力，这种理论称为有力矩理论或弯曲理论。经分析发现，薄壁壳体中，弯曲应力与周向应力相比较是一个很微小的数值。为了简化计算，采用无力矩理论的假定，其计算结果的精度同样可以满足工程需要。
1.无力矩理论的基本方程
（1）微元平衡方程
要研究回转薄壁壳体某一点a的应力，需要在该点取微元体。如图3-4a所示，用两个夹角为dθ的经线截面1截取回转壳体，再用过经线上的某点a及相邻点b的法线分别绕回转轴OO′旋转一周而形成的锥截面2截取回转壳体，得到微元体abcd（图3-4b）。
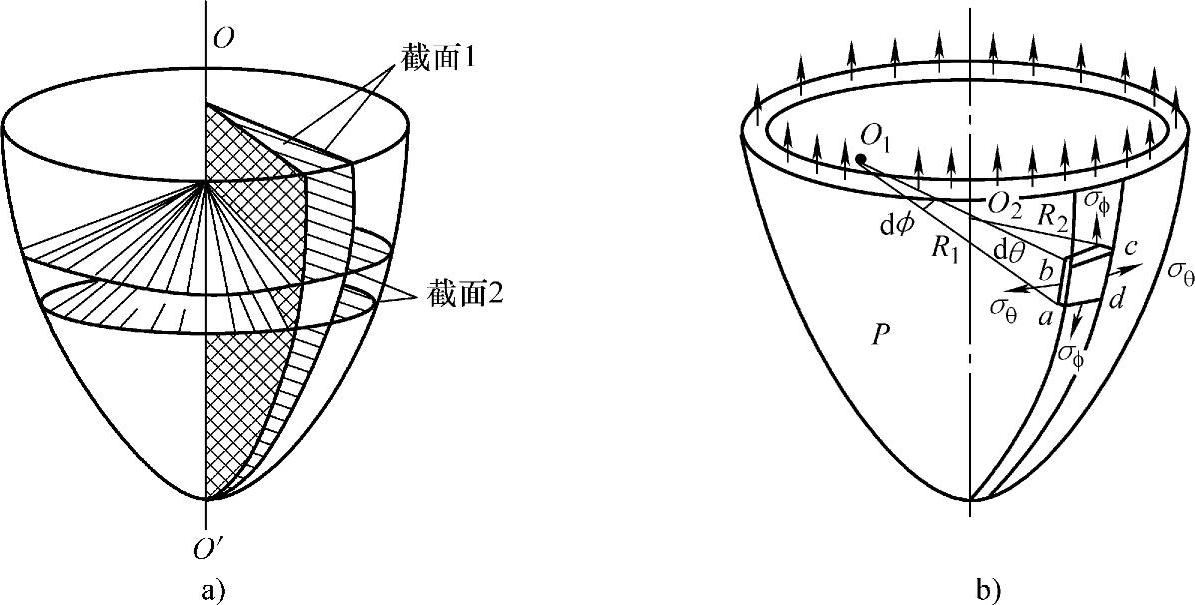
图3-4 微元体的取法及微元体应力
根据薄膜理论的分析，微元体abcd的截面ab和cd上有周向薄膜应力σθ，截面ad和cb上有经向薄膜应力σϕ。在微元体中心建立直角坐标轴XYZ，如图3-5所示。
由图3-5a可知，截线ad长dl2=rdθ，截线bc长dl2′=（r+dr）dθ，其截面上经向薄膜力分别为σϕtrdθ，（σϕ+dσϕ）t（r+dr）dθ，在Z轴投影和为（图3-5b）
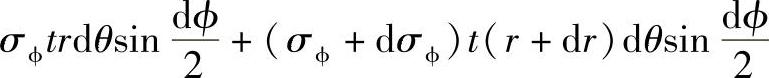
经线ab、cd弧长均为dl1=R1dϕ，经线ab、cd所在截面的周向薄膜力均为σθtR1dϕ，在同一平行圆上，将其合成，得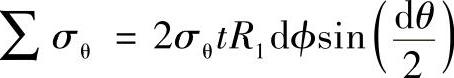
，如图3-5c所示，在Z轴投影（图3-5b）为
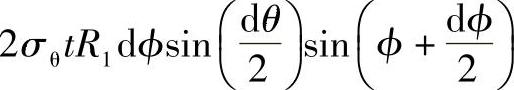
abcd的面积：dA=R1rdϕdθ
压力载荷p在Z轴的投影：pR1dϕrdθ
建立微体中上述力在Z方向的力平衡方程：
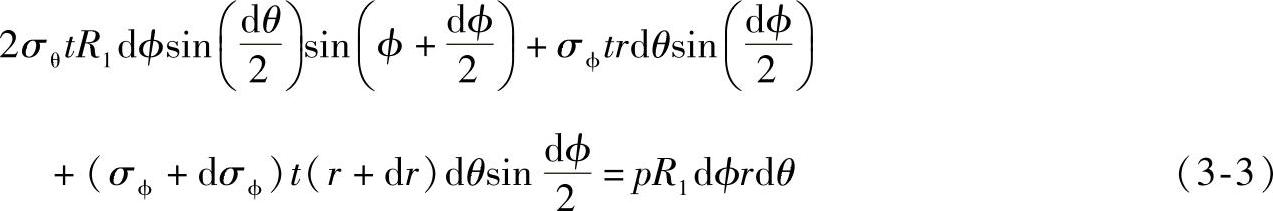
忽略高阶微量，且sin（dϕ/2）=dϕ/2、sin（dθ/2）=dθ/2，考虑式（3-1）r=R2sinϕ化简得
式（3-4）即为微元体平衡方程式或称拉普拉斯（Laplace）方程式。
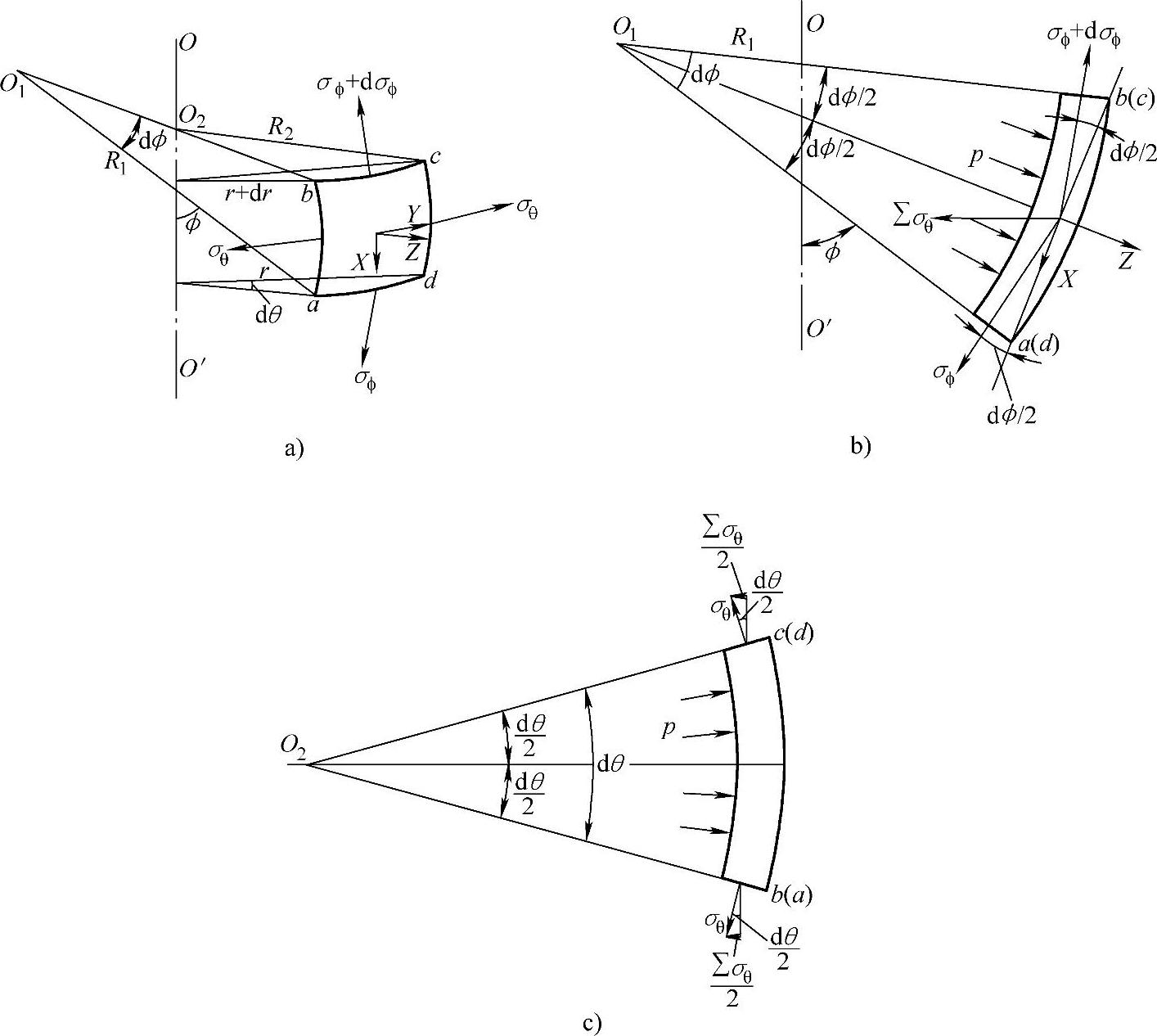
图3-5 微元体的应力分析
（2）区域平衡方程
以经线上一点M的法线绕回转轴旋转一周形成的锥截面M—M截取回转壳体（图3-6）。保留截开的壳体下部研究，压力载荷垂直于壳壁。壳体截面处各点内力沿经线的切向，为经向应力σϕ沿壳体载面一周作用的内力。
压力在回转轴方向产生的合力为
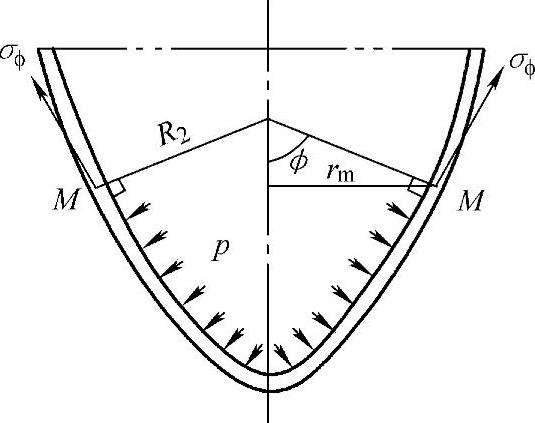
图3-6 区域平衡分析
作用在截面M—M上内力的轴向分量为
V′=2πrmσϕtsinϕ （3-6）
截开后保留的壳体部分内力与外力在轴向达到平衡，即所谓的区域平衡关系式：
V=V′=2πrmσϕtsinϕ （3-7）
由上式可求得σϕ，代入拉普拉斯方程可解出σθ。微元平衡方程式（3-4）与区域平衡方程式（3-7）是无力矩理论的两个基本方程。求解回转壳体的薄膜应力关键在于求V。
2.受均匀气体内压作用的回转薄壁壳体的薄膜应力
回转薄壁壳体仅受气体内压作用时，各处的压力p相等，压力产生的轴向力V为
由式（3-7）得
将式（3-9）代入式（3-4）得
（1）薄壁圆筒壳（图3-7）
薄壁圆筒中各点的第一曲率半径和第二曲率半径分别为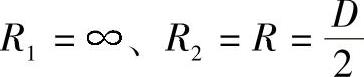
，将曲率半径
R1、R2代入式（3-9）和式（3-10）得
有 σθ=2σϕ
可见，薄壁圆筒中，周向应力是轴向应力的2倍。所以在筒体上开椭圆孔时，从受力的角度考虑，其长轴应垂直于筒体轴线，如图3-8所示。
（2）球壳
球形壳体上各点的第一曲率半径与第二曲率半径相等，即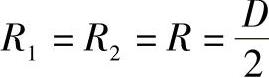
，将曲率半径代入式（3-9）和式（3-10）得
可见球壳的两向薄膜应力相等，为圆筒壳中周向应力σθ的一半。
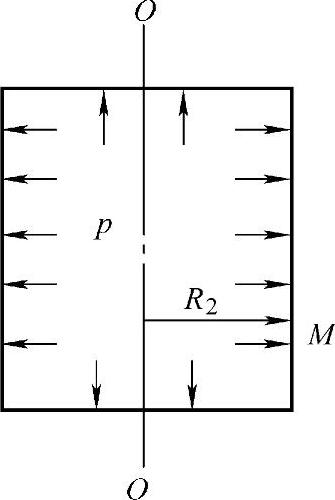
图3-7 受内压作用的圆筒形壳体
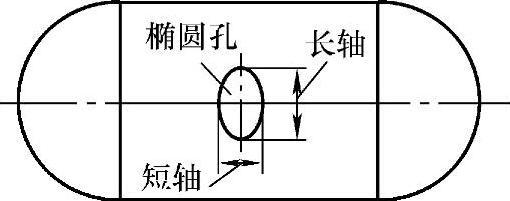
图3-8 圆筒上的椭圆开孔
（3）锥形壳体（图3-9）
锥形壳体中，R1=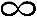
，R2=r/cosα=xtanα，代入式（3-9）和式（3-10）得
由式（3-13）可知周向应力和经向应力与x呈线性关系，锥顶处应力为零，离锥顶越远应力越大，且周向应力是经向应力的两倍。锥壳的半顶角α是确定壳体应力的一个重要参量。当α趋于0°时，锥壳的应力趋于等于圆筒壳体应力；当α趋于90°时，锥体变成平板，应力趋于无限大。所以在设计制造锥形容器时，α角要选择合适，不宜太大。同时还可以看出，周向应力和经向应力是随r改变的，在锥形壳体大端处，应力最大，在锥顶处，应力为零。因此，一般在锥顶开孔。(www.xing528.com)
（4）椭球形壳体（图3-10）
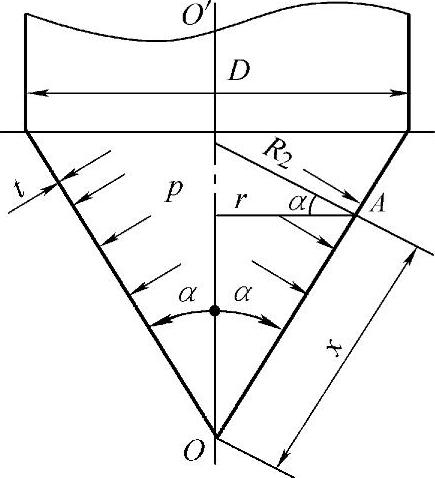
图3-9 锥形壳体的应力
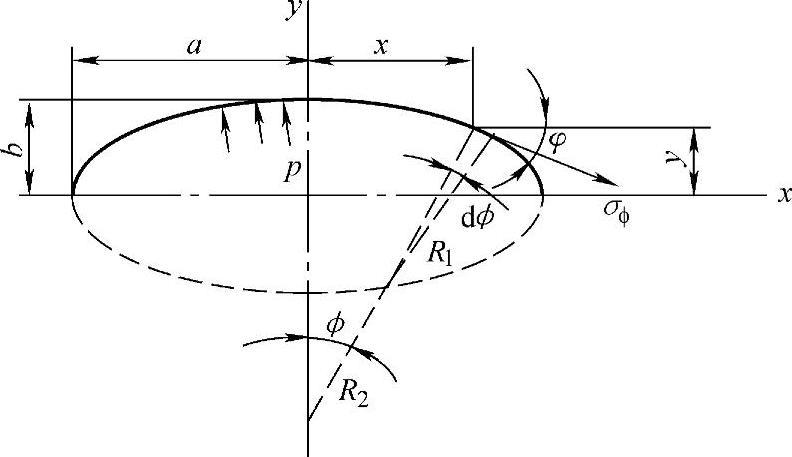
图3-10 椭球形壳体
由椭圆曲线方程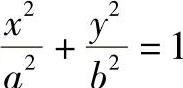
，得
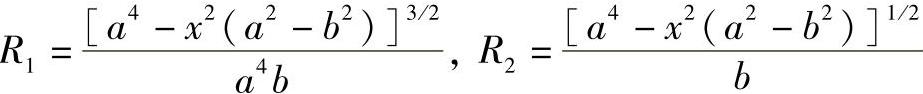
将R1、R2代入式（3-9）和式（3-10）得
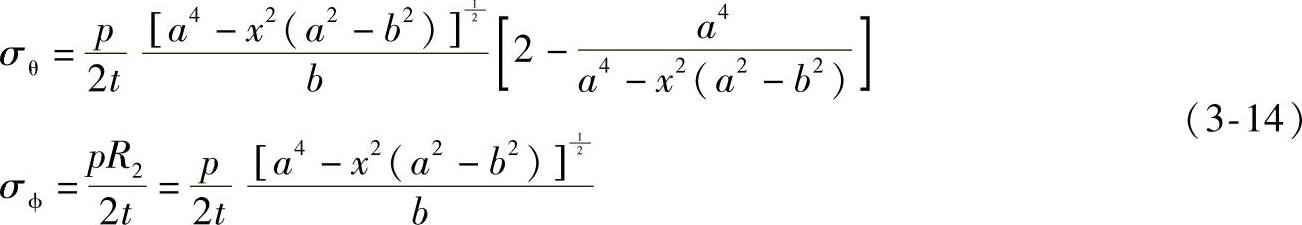
式（3-14）又称胡金伯格方程。
可以看出：椭球壳上各点的应力是连续变化的，其值与各点的坐标有关。椭球壳应力还与长轴与短轴之比a/b有关，a=b时，椭球壳变成球壳。随着a/b值增大，椭球壳中最大应力增加，如图3-11所示。椭球壳承受均匀内压时，在任何a/b值下，σϕ恒为正值，即拉伸应力，且由顶点处最大值向边缘处（赤道）逐渐递减至最小值。当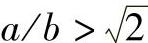
时，应力σθ将变号，从拉应力变为压应力。随着周向压应力的增大，大直径薄壁椭圆形封头赤道附近将出现局部屈曲，即局部失稳。为避免局部失稳的发生，可采取整体或局部增加厚度，局部采用环状加强构件等措施。
图3-11 椭球壳中的应力随长轴与短轴之比的变化规律
工程上常用标准椭圆形封头，其a/b=2。σθ的数值在顶点处和赤道处大小相等但符号相反，即顶点处为pa/t，赤道上为-pa/t，σϕ恒为拉应力，在顶点处达最大值为pa/t。此种封头由于应力水平总体不高，而制造较为方便，应用较为广泛。
3.受液体静压回转薄壁壳体的薄膜应力
受液体静压的回转壳体，液体的压力垂直于壳壁，各点的压力值随液体的深度而变，离液面越远，所受的液体静压越大。下面分别讨论圆筒在底部支承和上部支承两种情况下以及上部悬挂支承圆锥壳应力的表达式。
（1）底部支承的圆筒
图3-12所示为一底部支承的密闭圆筒，筒壁上任一点M的压力为
p=p0+ρgx （3-15）
式中 p——筒壁上任一点M处的液体压力（MPa）；
p0——液面上方的气体压力（MPa）；
ρ——液体密度（kg/m3）；
g——重力加速度（m/s2）；
x——M处距离液面的深度（m）。
忽略壳体质量，由于圆筒的R1=
，R2=D/2，根据微元平衡方程（3-4）可得
为了求壳体的经向应力，用过M点的横截面将壳体截开，考虑上部壳体的轴向力平衡。对于底部支承的圆筒，由于液体的重量由支承传递给基础，液体在圆筒壁不施加轴向力，只有气体压力p0产生轴向力，则横载面上部的壳体所受轴向外力
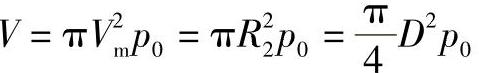
过M点的法线与回转轴ϕ=90°，轴向内力V′=2πrmtσϕsinϕ=πDtσϕ，由式（3-7）得
若为敞口容器，则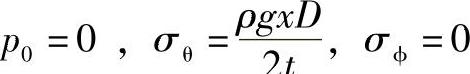
。
（2）上部支承的圆筒
图3-13所示为一上部支承的密闭圆筒，由于筒壁上任一点M处的液体压力与支承方式无关，所以其周向应力同底部支承的圆筒周向应力：
为了求壳体的经向应力，用过M点的横截面将壳体截开，考虑下部壳体的力平衡。对于上部支承的圆筒，除了气体压力p0产生轴向力外，液体的液柱静压也使圆筒壁受轴向力作用，则
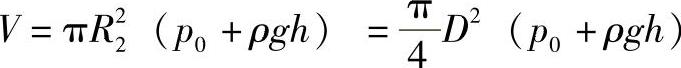
过M点的法线与回转角交角ϕ=90°，V′=2πrmtσϕsinϕ=πDtσϕ，由区域平衡关系式（3-7）得
若为敞口容器，则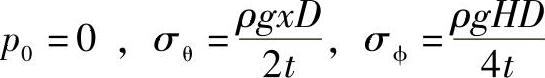
。
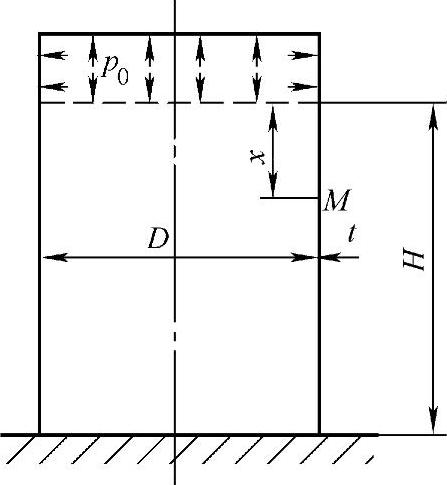
图3-12 底部支承的圆筒
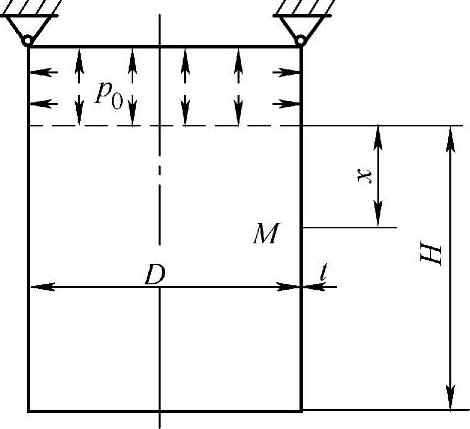
图3-13 上部支承的圆筒
（3）上部支承的敞口圆锥壳应力极值
图3-14a为一上部支承的敞口圆锥壳，忽略锥壳质量。R1=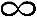
，R2=ytanα/cosα壳体上任一点M处的压力为
p=ρg（H-y）
将R1、R2代入（3-4）得
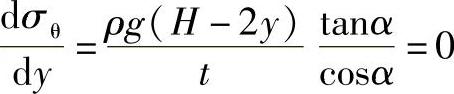
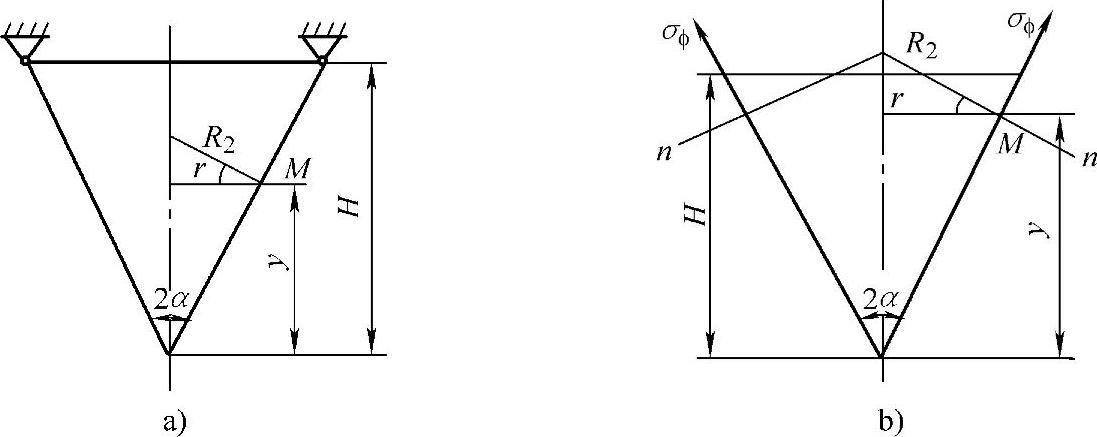
图3-14 上部支承的锥壳
解得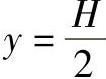
将y代回式（3-20）可得
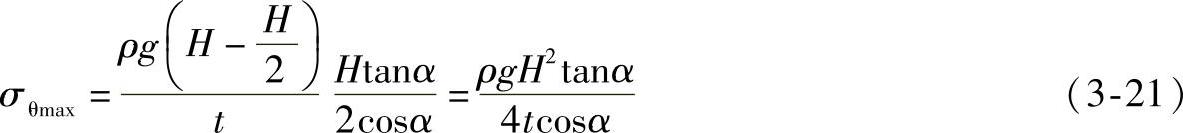
再用过M点的法线为母线绕回转轴旋转而成的锥截面n-n，将锥壳截开（见图3-14b），求解经向应力。考虑下部分壳体的力平衡，液体静压作用在这部分壳体的轴向外力为
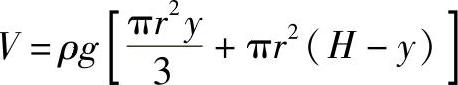
过M点的法线与回转轴交角ϕ=90°-α，轴向内力V′=2πrmtσϕsinϕ=2πrtσϕcosϕ，由区域平衡关系式（3-7）得
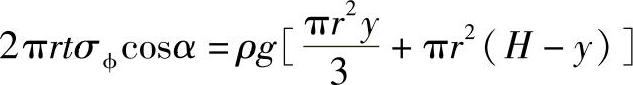
由r=ytanα推得
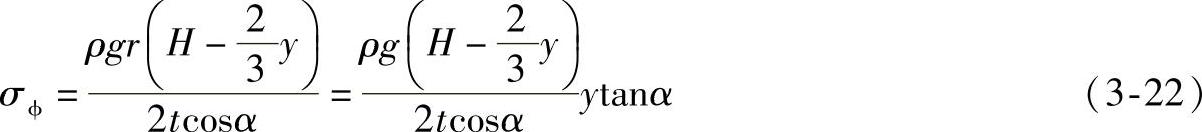
对上式求导，并令其一阶导数为零，得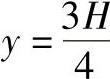
，则
比较式（3-21）和式（3-23）可见，在液体压力作用下，锥壳的两向应力的最大值不在同一位置。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
