塑化过程螺杆计量段三维流场数值模拟优化

塑化过程螺杆计量段三维流场的数值模拟^[76]

马德君，陈晋南

注塑螺杆的塑化过程就是熔体的输送过程，即熔体的计量过程。目前，该过程普遍按照挤出机的熔体输送机理进行近似的研究，与注塑机中的真实状况有较大的偏差。本文采用CROSS模型表示聚氯乙烯(PVC)熔体的黏度特征，使用Polyflow软件分别数值模拟了塑料注塑成型机头部无螺纹和有螺纹的螺杆计量段流道内PVC熔体在塑化过程的三维等温流场，求解和分析了不同时刻两种不同螺杆计量段的速度场、剪切速率场、黏度场和剪切应力场，研究了注塑螺杆的挤出机理，以期对注塑螺杆的设计和聚合物加工提供理论指导。

1注塑机计量段的几何构型

根据机筒静止、螺杆旋转并周期性往复运动的条件，建立螺杆计量段流道的三维有限元模型。注塑螺杆的行程为150mm，本文对塑化阶段最初75mm行程的流场进行模拟研究。选取机筒314mm的局部为流体域，选取注塑螺杆计量段232mm的局部作为计算域，以螺杆初始位置时入口端截面的圆心为原点，以螺杆中心轴线为z轴建立直角坐标系。图1(a)给出了头部不带螺纹的注塑螺杆（以下简称为螺杆元件1）的几何造型，图1(b)给出了头部带螺纹的注塑螺杆（以下简称为螺杆元件2）的几何造型。

为了提高计算的精度，在GAMBIT中对机筒的边界层进行了加密，采用八点六面体单元网格划分机筒，采用四面体单元网格划分注塑螺杆。再将划分网格的螺杆和机筒组合在一起。由于螺杆的运动导致流道的形状随时间变化，需要在每一个时刻重新生成流道实体并对其划分网格。为了克服因螺杆运动而带来网格划分的重复工作量，使用Polyflow软件包提供的网格叠加技术来生成有限元网格。

图1 注塑螺杆的几何造型

(a)螺杆元件1 (b)螺杆元件2

2 数学模型

假设聚合物熔体为不可压缩流体，流动为等温拟稳态流动，流道全充满。由于聚合物熔体的高黏性，惯性力和质量力相对于黏性力很小，忽略不计。假设机筒内壁和螺杆表面无滑移。在以上假设条件下，描述流场的基本微分方程有：

连续性方程

运动方程

本构方程

CROSS方程

式中，u为速度向量，p为压强，τ为应力张量，D为形变速率张量，η₀为零剪切黏度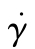，为剪切速率，t_λ为自然时间，m为指数。

数值计算中采用的工艺条件由某企业提供，数值如下：塑化时螺杆转速95r/min，退行速度7.5mm/s，螺杆行程75mm，入口压强为5MPa，出口压强随时间呈线性变化，遵循公式y＝－82.5+4.25t(MPa)，t为塑化时间。塑化熔料PVC的物性参数η₀＝3.32×10⁴Pa·s，t_λ＝0.2288s，m＝0.7438。

网格生成后，在GAMBIT中定义边界条件，然后导入POLYDATA。在POLYDATA中输入计算初始条件和其他计算参数，使用软件POLYFLOW3.10在HP xw6000工作站上完成全部计算工作。计算的收敛精度设为10^－4，完成所有计算需要两周时间。

3 结果与讨论

根据数值计算的结果，本文重点分析了塑化时刻t＝0.1，2.1，4.1s的流场，讨论了螺杆与机筒的组合流道的yz平面上和xy截面上的流场。图2给出了yz平面和三个xy截面A—A(z＝0.050m)、B—B(z＝0.140m)和C—C(z＝0.230m)截面在流场中的位置。通过对数值计算结果的分析，发现在yz平面上t＝2.1，4.1s时两种螺杆元件产生的流场基本相同，文中仅给出了t＝0.1，4.1s两个时刻yz平面上的流场；在xy截面上仅给出了头部螺纹对PVC熔体流场影响比较显著的t＝0.1s时的流场。图3-6给出了典型的计算结果。

图2 参考面在流场中的位置

3.1 速度场(www.xing528.com)

图3给出了在塑化时间t＝0.1，4.1s时两种螺杆元件yz平面内的z方向分速度场，熔体区域图中的曲线为速度等值线。对于两螺杆元件，头部熔体均产生逆流，螺棱顶部产生漏流。随着塑化的进行，对于螺杆元件1，塑流速度最大值约是螺杆退行速度的2倍；漏流速度最大值略小于螺杆退行速度；螺槽中PVC熔体正流速度比较稳定，速度最大值约是螺杆退行速度的5倍。头部速度等值线比较均匀，形状规则上下基本对称。另外，随塑化的进行，螺杆头部等值线变得稀疏，表明速度梯度减小。

在t＝0.1s时，可看出螺杆头部的螺纹对z方向分速度场产生明显的影响，螺杆元件2螺杆头部附近熔体的逆流速度最大值出现在头部螺棱的顶部，是螺杆元件1头部逆流速度最大值的2.6倍；随着塑化的进行，逆流速度最大值减小，到4.1s时降低了65%，小于4.1s时螺杆元件1的最大值。螺杆元件2的螺槽中PVC熔体运动速度随时间没有明显变化。由此可见，螺杆头部螺棱的存在明显改变了PVC熔体的逆向流动，延长了物料的塑化时间，提高了螺杆的挤出质量。

图3 在不同时刻两种螺杆元件yz平面上的z-速度场

(a)螺杆元件1 (b)螺杆元件2

同时，对t＝0.1s时两种螺杆元件在xy截面上的z方向分速度场也进行了分析。在A—A截面上，两种螺杆元件在螺棱顶部均存在漏流，螺杆元件1漏流速度的最大值约是螺杆元件2的2倍。两种螺杆元件在螺棱以外的区域均以正流为主，速度差别不大。螺杆元件1的B—B截面与A—A截面的速度场相比，速度等值线比较稀疏，螺杆附近区域逆流最大值没有变化，螺槽中正流速度最大值减小30%，与螺杆元件2的速度场相比差别显著。由于螺纹的存在，螺杆元件2的B—B截面与A—A截面的速度场相比，漏流速度最大值增加13倍，螺槽中正流速度最大值略有减小，速度梯度明显增大。在C—C截面上，两种螺杆元件均表现为逆流，螺杆元件1中的速度最大值略大于螺杆元件2。

3.2 压强场

首先对t＝0.1，4.1s时两种螺杆元件yz平面内的压强场进行了分析对比。螺杆元件1仅在头部熔体的压强指向负z方向，并在螺杆头中部形成一个负高压区域。从0.1s到4.1s，该区域的压强值降低40%。另外，等值线分布较均匀，上下对称形状规则，说明压强值平稳变化；随塑化的进行，在螺杆不断向后移动的同时，压强等值线变得稀疏。由于螺杆头部增加了螺纹，螺杆元件2与螺杆元件1相比螺杆头部螺纹附近的压强等值线形状不规则、上下对称性较差，并在螺杆头螺棱后缘面形成一个负高压区域，其最大值是螺杆元件1的2倍。随塑化的进行，螺杆元件2在4.1s时压强值降低80%。

图4给出了t＝0.1s时两种螺杆元件在xy截面上的压强场，熔体区域图中的曲线为压强等值线。从图4中看到，在A—A截面上，两种螺杆元件的压强场等值线分布与形状比较一致，均为正值，螺杆元件1的压强最大值是螺杆元件2的1.3倍。在B—B截面上，两种螺杆元件均出现正值和负值。螺杆元件2在螺棱附近产生负压的最大值是螺杆元件1的5倍；螺杆元件2的正压最大值只有螺杆元件1的40%。在C—C截面上，两种螺杆元件均产生负压，螺杆元件1的最大值是螺杆元件2的1.4倍。

图4 两种螺杆元件xy平面上的压强场

(a)螺杆元件1 (b)螺杆元件2

3.3 剪切应力场

图5给出了在塑化时间t＝0.1，4.1s时yz平面上两种螺杆元件的剪切应力场，熔体区域图中的曲线为剪切应力等值线。从图5中可以看出，螺杆元件1在螺棱顶部的剪切应力最大，出口中心处剪切应力最小，而且在塑化过程中保持不变。由于螺纹的存在，使在0.1s时螺杆元件2头部的最大剪切应力出现在螺棱顶部，是螺杆螺棱的80%，是螺杆元件1的1.5倍。随着塑化的进行，螺杆元件2头部的PVC熔体承受的最大剪切应力从0.1s时的0.659MPa减小到4.1s时的0.330MPa，与螺杆元件1的区别越来越小。由于螺杆头部增加螺纹以后，速度场发生明显变化，引起速度梯度场和压强场的变化，从本构方程(3)中可以看出，当PVC熔体的速度梯度和压强值减小时，剪切应力随之降低。

计算时，对t＝0.1s时两种螺杆元件在xy截面上的剪切应力场也进行了分析，比较了各个截面剪切应力的值，在A—A截面上的螺棱顶部，两种螺杆元件的剪切应力没有明显区域。在B—B截面上的筒壁附近，螺杆元件1最大剪切应力是A—A截面上的0.5倍。由于螺杆头螺纹的存在，螺杆元件2在B—B截面上和A—A截面上的剪切应力场近似，螺杆元件2剪切应力最大值是螺杆元件1的2倍。在C—C截面上，螺杆元件1的剪切应力最大值是螺杆元件2的1.7倍。这进一步说明，由于螺杆头部增加螺纹后，流速场发生明显变化，引起速度梯度和压强场的变化，由本构方程(3)可以看出，当PVC熔体的速度梯度和压强值增大时，剪切应力值随之增大。

3.4 黏度场

对t＝0.1，4.1s时刻两种螺杆元件的yz平面上的黏度场进行分析，得知两种螺杆元件的最大黏度均出现在出口中心区域，最小值出现在螺棱附近。随着塑化的进行，熔料的黏度略有增大。从CROSS黏度方程可知，黏度η随着剪切速率减小而增大。图6给出了t＝0.1s时刻两种螺杆元件在B—B截面上的黏度场。从图6可以看出，螺杆头部的螺棱使B—B截面上黏度的最大值从17623Pa·s减小到6538Pa·s，更加有利于PVC熔体的进入模具的流动。由剪切应力场的分析，可知在B—B截面螺杆元件2的剪切应力大于螺杆元件1，这是黏度值降低的一个原因。

图5 不同时刻两种螺杆元件在yz平面上的特征剪切应力场

(a)螺杆元件1 (b)螺杆元件2

图6t＝0.1s时B—B截面上的黏度场

(a)螺杆元件1 (b)螺杆元件2