数值模拟汽车密封圈口模内的非等温流动优化方案

数值模拟汽车密封圈口模内的非等温流动^[69]

陈晋南，胡敏，吴荣方

引言

随着计算机和计算方法的飞速发展，科学计算已经与理论研究和试验研究并列成为科学研究的重要方法。利用计算流体力学数值模拟研究橡胶熔体在模具中的流动行为，可优化加工过程，调控产品的结构和性质，有助于实现加工的自动化控制，提高劳动生产效率。2007年，戴元坎等采用纯黏性模型数字设计了简单口型，用试验验证了数值模拟结果。郭吉林等数值研究了物料黏弹性和工艺参数对橡胶异型材挤出胀大的影响。柳和生等采用PPT黏弹性模型数值模拟了L型挤出口模内聚合物熔体的三维等温流动。朱敏采用Carreau模型数值研究了口模内橡胶熔体的等温流动。

本文使用聚合物计算流体力学软件Polyflow，数值计算了F01型汽车密封圈挤出口模内和离模后橡胶熔体的三维等温和非等温流场，讨论温度对口模结构和橡胶熔体流变行为的影响，为模具设计提供了理论依据和技术支持。

1 数学物理模型和计算方法

用幂率模型和近似Arrhenius式的乘积描述橡胶表观黏度的本构方程为

式中，η为表观黏度，Pa·s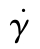；为剪切速率，s^－1；T为温度，K；t₀为自然时间，s；K为黏稠系数，Pa·s；n为非牛顿指数，1；β为Arrhenius指数；T₀为参考温度，373K。使用Polymat软件拟合实验测试数据，确定本构方程式(1)中的系数，t₀为130s；K为2592449.1Pa· s；n为0.214；β为0.00617。

根据F01型汽车密封圈口模内橡胶的流动情况，假设橡胶熔体为不可压缩纯黏性非牛顿流体，口模内的熔体是三维非等温稳态流动，流道全充满，流道壁面无滑移。橡胶熔体是高黏度流体，黏性力远大于惯性力和质量力，后者可忽略。描述F01型汽车密封圈口模内橡胶熔体流动的控制方程为：

连续性方程

运动方程

应力张量

变形速率张量

能量方程

黏性热

式中，u为速度，m·s^－1；p为压力，Pa；I为单位张量；τ应力张量，Pa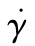；为剪切速率，s^－1；D为变形速率张量，s^－1；ρ为密度，1600kg·m^－3；导热系数κ为0.15J/(m·K)；c_p为比热容，取值为2400J/(kg·K)；ϕ为黏性热，W·m^－3。

根据实际产品截面尺寸，逆向挤出设计F01型汽车密封圈口模，建立其几何模型，如图1(a)所示。选取橡胶熔体ACDF为模拟研究对象，坐标原点选在口模进口截面的右下角，流体流动方向为z轴，其中口模ABEF长15mm和挤出橡胶熔体BCDF长25mm。用四面体网格划分熔体ACDF。在口模出口和壁面附近熔体流场变化剧烈处网格适当加密，网格总数为17350个。图1(b)给出了F01型汽车密封圈口模的网格划分。

采用橡胶表观黏度的本构方程(1)，设置进口体积流量为q_V＝3.5×10^－5m³·s^－1，等温的条件为进口、壁面和出口温度为373K，非等温的条件为进口温度为373K，出口和自由表面温度为303K。采用有限单元法，使用Polyflow软件，流速采用Mini-element插值，压力采用线性函数，能量方程采用上风法插值，黏度采用皮卡迭代。引入罚函数项修正动量方程(3)和能量方程(6)，将连续性方程(2)作为求解动量方程的一个约束条件，用隐式欧拉法联立数值求解离散化非线性耦合的控制方程式(1)~(7)，分别数值模拟F01型汽车密封圈橡胶熔体的口模等温和非等温挤出过程，计算了口模内外橡胶熔体的等温和非等温流场，比较了等温与非等温流场的各物理量，讨论了温度对熔体的速度、压力、剪切应力和黏度等物理量的影响。在HPXW6000工作站上完成全部的计算，计算的收敛精度为10-3，最长一次运算机时为10h。

图1 几何模型和网格划分

(a)口模的几何模型(b)几何模型ACDF网格划分

2 结果与讨论

为了深入地分析温度对口模挤出过程的影响，计算了口模内和离模后橡胶熔体等温和非等温流场各物理量平均值沿挤出方向的变化。横截面上各物理量的平均值定义为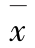(www.xing528.com)

式中，x分别代表了温度，流速、压力，剪切应力和黏度等物理量。

下面分两部分讨论了数值研究的结果。

2.1 流道内熔体的非等温流场

为了考察口模内和离模出口处的熔体温度变化，图2(a)和(b)分别给出了z＝9mm和z＝40mm横截面上橡胶熔体的温度场。由图2可知，在口模内部横截面上熔体的温度变化不大，在出口横截面上温度变化较大，温度差为62K。因此考虑温度对离模后熔体流场的影响是必要的。

图2 横截面橡胶熔体的温度场，K

(a)z＝90mm横截面，K(b)z＝40mm横截面，K

图3(a)、(b)、(c)和(d)分别给出了z＝9mm横截面熔体的黏度场、速度场、压力场和剪切应力场，由图3(a)~(d)可知，截面上熔体的黏度、速度和压力均在截面中心区域最大，向外逐渐减小，剪切应力从中心区域向外逐渐增大。口模截面黏度差为11kPa·s，熔体的速度差为0.27m/s，压力差为0.22MPa，剪切应力差为0.65MPa，最大剪切应力出现在截面上的拐角处。橡胶熔体在高剪切速率下黏度降低，出现剪切变稀的现象。

2.2 熔体非等温与等温流场的物理量比较

沿z轴每间隔3mm截取口模横截面，用公式(8)分别计算了等温和非等温流场的横截面物理量的平均值。图4给出橡胶熔体平均温度沿z轴的变化。由图4可知，在蛎等温条件下，沿着熔体流动的方向，熔体受到模具阻力，在口模内(z＝0~15mm)熔体的温度略微升高，熔体离模后受环境温度的影响，其平均温度降低到349K，由于温度降低熔体黏度变大，黏性生热效应显著，温度在急剧下降之后出现缓慢的回升。

橡胶熔体在口模内沿着熔体流动方向，等温和非等温熔体的平均压力均降低，非等温熔体平均压力略高于等温熔体，但差别不是很大。熔体离模后受到环境温度影响，非等温和等温流体速度和压力不相等。图5(a)和(b)分别给出z＝18mm橡胶熔体的等温和非等温的平均压力和平均速度沿z轴的变化。沿着熔体流动的方向，由于熔体离模后温度降低，熔体黏度增大，其黏滞力增强，非等温熔体的平均速度小于等温熔体，平均压力低于等温熔体。在z＝21mm处，非等温熔体和等温熔体的平均压力均出现最低点，此时熔体对外界有一定的压力，且在此处达到最大。在z＝24mm处等温和非等温熔体的平均速度趋于一个定值，非等温熔体的平均速度比等温的小了5%，非等温熔体的平均压力比等温的小了8%。

图3 口模内z＝9mm截面橡胶熔体的流场

(a)橡胶熔体的黏度场，Pa·s (b)橡胶熔体的速度场，m/s (c)橡胶熔体的压力场，MPa (d)橡胶熔体的剪切应力场，Pa

图4 口模内外橡胶熔体的平均温度沿口模z轴的变化

图5 口模外橡胶熔体的平均速度和平均压力沿口模z轴的变化

(a)平均压强，kPa (b)平均速度，m/s

在z＝18mm处，等温和非等温熔体的平均黏度和平均剪切应力的差别不是很大，从z＝30mm开始有较大差异。图6(a)和(b)分别给出z＝30mm等温和非等温的橡胶熔体平均黏度和平均剪切应力沿z轴的变化。沿着熔体流动的方向，等温和非等温熔体的黏度上升，剪切应力下降，非等温熔体的平均剪切应力和平均黏度均略大于等温熔体。在z＝36mm处非等温熔体的平均剪切应力比等温的大3%，平均黏度比等温熔体大5%。

图6 口模外橡胶熔体的平均黏度和剪切应力沿口模z轴的变化

(a)平均黏度，MPa·s (b)平均剪切应力，kPa

3 结论

本文使用polyflow软件，用幂率模型和近似Arrhenius式的乘积描述橡胶表观黏度的本构方程，分别数值求解了F01型汽车密封圈口模内外橡胶熔体的非等温和等温流场，研究了熔体的非等温流场中各物理量的分布，分析讨论了温度对橡胶口模挤出过程的影响。结果表明，在口模内，横截面上橡胶熔体的速度、压力和黏度均从中心区域向截面周围逐渐减小，剪切应力从中心区域向截面周围逐渐增大。横截面上中心处橡胶熔体的速度最大，截面拐角处速度最小。沿着熔体流动的方向，平均压力降低。等温熔体和非等温熔体流场差别不大。离模后，非等温熔体受到环境温度的影响，温度骤降。由于温度降低后熔体黏度变大，黏性生热铲应显著，温度急剧地下降之后出现缓慢的回升。由于温度和剪切速率的综合影响，熔体的平均黏度逐渐升高。沿着熔体的流动方向，离模后熔体的平均黏度增大，剪切应力降低。非等温熔体的平均剪切应力和平均黏度都略高于等温熔体，平均速度小于等温熔体。温度较大影响熔体离模后的平均速度。挤出产品截面和实际产品截面尺寸误差很小，采用幂率模型和近似Arrhenious式乘积的非等温本构方程数值模拟更接近口模挤出的实际情况。