数值模拟聚合物加工成型过程的基本方法

目前，各国广泛地使用成熟的Polyflow软件数值模拟仿真聚合物的加工成型过程，模拟仿真聚合物熔体的流变行为，从两个方面研究聚合物加工成型机理：

① 在设备结构一定的条件下，拟合物料流变测试的数据，确定物性参数和本构方程，研究物性参数和工艺条件对聚合物材料加工成型的影响；

② 在物性参数和本构方程一定的条件下，数字设计螺杆、模具等设备，数值研究设备结构和工艺条件对聚合物材料加工成型的影响。

由于在一台螺杆挤出机上可完成输送、混合、捏合、塑化和挤压等过程，螺杆挤出机从上个世纪问世以来，在聚合物、生物、食品加工方面得到了广泛应用。聚合物螺杆挤出过程已成为世界范围内的研究热点。在聚合物加工成型领域中，双螺杆挤出机作为一种连续混合设备，以其诸多的优点而具有很大的应用市场。

本小节以螺杆挤出加工成型为例，介绍数值模拟聚合物材料加工成型过程的基本知识，包括聚合物材料加工成型的控制方程、数值模拟聚合物材料加工成型过程的相关知识、数值研究聚合物加工成型问题的基本步骤和方法、使用软件数值模拟聚合物加工成型过程容易出现的错误等4部分。

定量研究聚合物材料加工成型过程，预测过程的特性，需对加工聚合物材料的过程模型化。数学模型是物理系统的理想数学描述，它用数学语言表达了过程诸物理变量和自变量之间的关系，是计算机数值计算模拟的基础。

根据聚合物螺杆或模具加工成型过程的特点，假设：

① 螺杆或模具流道内全充满高黏度聚合物材料熔体，在每一流道横截面均为充分发展的流体流动；

② 流体流动速度缓慢，属于小雷诺数流动，忽略惯性力和质量力；

③ 熔体为不可压缩流体，ρ为常数；

④ 熔体稳定流动，所有的物理量不随时间变化，方程中不含时间自变量＝0；

⑤ 熔体流动为稳定不可压缩的层流，不存在涡旋流动，即u·▽u＝0；

⑥ 根据具体问题，决定流体对固体壁面无滑移或有滑移的条件；

⑦ 由于设备流道横截面尺寸大大小于流动方向的长度，因此横截面的速度梯度较流动方向的速度梯度大得多；

⑧ 由于熔体的流动，流动方向的对流传热大于热传导，视设备的加热情况，给出壁面温度的边界条件；

⑨ 熔体的导热系数和热扩散系数为常数。

基于以上假设，具体简化第3.3.1节黏弹性不可压缩流体简化的控制方程(3.3.6)，得到描述螺杆或模具流道聚合物熔体流动控制方程

连续性方程

运动方程

本构方程

或

能量方程

黏性热

式中，u为速度向量，m/s；p为压力，Pa；I为单位张量；τ为应力张量，Pa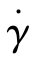；为剪切速率，s^－1；D为变形速度张量，s^－1；η为黏度，Pa·s；η₀为零剪切黏度，Pa·s；τ_y为屈服应力，Pa；为临界剪切速率，s^－1；t_λ为松弛时间，s；n为非牛顿指数（幂律指数）；b为热敏系数（温度修正系数），K^－1；T₀为参考温度，即测试温度，K；T为任意温度，K；c_p为比热容，J/(kg·℃)；κ为导热系数，W/(m·K)；Φ为黏性热，Pa·s^－1。

这里注意几点： a.软件中，变形速度张量用D表示，热敏系数β用b表示；b.式(9.1.5a)和式(9.1.5b)给出本构方程的例子。根据具体问题，使用第5.3节介绍的方法在软件中选择合适的本构方程；c.如果研究等温问题，不需要考虑能量方程。

描述聚合物材料实际加工成型过程的控制方程(9.1.1)至式(9.1.7)是耦合的非线性偏微分方程组，不能求解析解，只能数值求解。由于在螺杆流道内，聚合物熔体的流动是黏性流体的小雷诺数层流，可以使用Polyflow软件。

这里以聚合物材料螺杆挤出加工成型为例介绍数值模拟的相关基本知识。本部分从数值模拟对象和问题、数学模型和求解域、数值模拟的迭代方法和计算精度等3个方面简介数值模拟的相关知识。

(1)数值模拟的对象和问题

根据工程的具体问题，确立数值模拟研究的对象和问题。根据研究的问题分类，聚合物螺杆挤出过程的数值模拟对象大致分为三方面。

① 螺杆功能段的数值模拟。在聚合物螺杆挤出加工过程的数值模拟中，相对于固体输送段、熔融段、排气段以及其他功能段，熔体计量段、捏合段、过渡段和输送段被研究得较多。因为在这些功能段，聚合物熔体的流动和传热可以由经典的理论来描述。聚合物螺杆挤出加工过程的数值模拟，所研究的内容是螺杆的几何参数、组合构造和操作工艺条件（螺杆转速、压力、温度、流量等）对流场的各个特征量（速度场、剪切速率场、应力场、压力场、温度场、黏度场、应变分布函数SDF、停留时间分布函数RTD等）和熔体输送特性参数（流量、回流量、扭矩、轴功率等）的影响规律。如图9.1.2所示。

② 螺杆混合特性的数值模拟。在聚合物的加工过程中，混合也是一个非常重要的方面。捏合块在一定程度上决定了双螺杆挤出机的混合效率。比如聚合物热的均化、相对分子质量分布的均化、排气和化学改性等都与混合分不开。对于物理改性中机械流变混合过程，一般将其分为两种，即分散性混合(dispersive mixing)与分布性混合(distributive mixing)。数值模拟双螺杆挤出螺杆元件的混合性能分两步：第一步算出流场；第二步利用已求出的流场特征量定义一些混合指标，由此来衡量各元件的混合性能。以长度拉伸比、面积拉伸比和应变分布等作为分布混合程度的衡量指标，使用粒子示踪技术数值研究分布混合情况。

③ 螺杆反应挤出的数值模拟^[16]。在共混反应挤出等领域，双螺杆挤出机得到了广泛的应用。反应挤出的研究是近年来的一大热点。由于双螺杆挤出流道流体的流动很复杂，若再与化学反应耦合，将使这一过程的数值模拟更加困难。假设物料已呈完全熔融状态，将双螺杆挤出流道作为该反应的生物反应器，将挤出流道看成一个封闭的管状系统，使用一级反应动力学方程式，数值模拟了生化反应，研究聚合物停留时间分布(RTD)的信息。在不同螺杆构造和不同工艺条件下，考察了聚合物单体沿着双螺杆流道轴向的转化率；忽略化学反应对体系黏度的影响，模拟聚合物双螺杆挤出过程的热降解反应，分析不同螺杆构造和螺杆转速对反应特性的影响；研究啮合同向旋转双螺杆挤出机作为三相反应器的工作特性，探讨将催化剂固定在螺杆表面的可行性；使用自清式双螺杆正向输送元件，研究过氧化物引发的一种商用聚丙烯树脂的降解反应，考察螺杆转速、入口处过氧化物分布和压力流与拖曳流之比对其混合特性的影响，研究重均相对分子质量的变化对反应体系黏度的影响，通过重均相对分子质量将剪切黏度与反应动力方程联系起来。

(2)数学模型和求解域(www.xing528.com)

数值模拟的首要条件是建立准确的数学模型和反映实际工程问题的边界条件。根据功能的不同，挤出螺杆被划分为不同的区段。不同的区段对应不同的流动和输送机理，用不同的数学型来描述各段的流动规律。在聚合物熔体不可压缩、流动状态为稳定层流流动、流道全充满、流道壁面无滑移或壁面滑移的假设条件下，建立双螺杆挤出聚合物的数学模型。

① 本构模型。早期的研究大多使用的本构模型是牛顿模型、幂律模型。虽然绝大多数聚合物熔体都是非牛顿流体，早期对双螺杆的模拟大都采用牛顿模型来简化分析。幂律模型是最简单的非线性模型，该模型能较准确地反映黏度曲线上的剪切变稀区域。但是，忽略了在较低和较高剪切速率时的牛顿平台区域，在低的剪切速率时，黏度趋于无穷大，而在高的剪切速率时，黏度趋近于零。在这两种情况下使用该模型导致模拟结果与实际情况有很大误差。Carreau模型能够准确地反映出较低和较高剪切速率的两个牛顿平台区以及中间的剪切变稀区域。因此，适用于较大的剪切速率变化范围。近年来，不少论文用了该模型。

当模拟非等温流动时，大多都使用Carreau模型和近似Arrhenius定律的乘积描述熔体表观黏度与温度、剪切速率的关系。也有使用Power或Cross模型与Arrhenius定律的乘积，描述熔体表观黏度与温度、剪切速率的关系。研究聚合物黏弹性流动问题常使用黏弹性PTT模型，例如用PTT模型描述ABS熔体的离模膨胀流变性质^[71]。

经过多年的发展和完善，Polyflow软件包涵了很多模型供使用，可以根据第5.3节介绍的本构模型选择的方法确定被研究聚合物的本构方程。

② 求解域、边界条件和网格划分。求解域的大小与计算机的内存有关。由于计算机的内存问题，早期的研究沿螺杆轴向截取一个螺槽流道、螺纹块和捏合块等螺纹元件作为研究对象，数值模拟一维或二维等温牛顿流体的流动，这样选取计算域比较直观便于分析。但是，由于使用数学模型过于简化的牛顿流体模型，计算域太短不足于反映真实问题。因此，研究的结果不能真实反映实际问题。20世纪末，陈晋南课题组最初仅购置了一个软件证书，仅能模拟螺杆一段螺纹元件的求解域。

2003年，陈晋南课题组使用SGI-O₂工作站和软件Polyflow3.7，数值模拟双螺杆挤出螺纹元件的三维等温流场，螺纹元件轴向长度是48mm，计算精度设定为10^－3，完成一次计算大约需要48h。陈晋南课题组购置了有8个核的计算工作站，购置了8个软件证书，可以并行运算，研究复杂聚合物加工成型问题。2012年，数值模拟螺杆长60mm、机筒内壁开有螺旋沟槽构成的混炼段的混合过程，计算相对误差不超过10^－3，完成一次计算大约需要8h。由此可见，尽管使用了8个核的工作站，数值计算域还是很短。需要建立大型计算工作站，资源共享必将推动塑料行业应用信息技术的深入和快速发展，最终推动行业新技术、新设备和新材料的创新发展。

边界条件反映实际问题的特性，对于数值计算的结果往往具有决定性的影响。双螺杆挤出流道的形状随着螺杆的转动而发生变化，使运动边界问题成为数值分析的一大难点。如果对流道形状的每一微小改变都重新进行网格划分，那么，工作量将会非常大。早期为解决这一问题，假设机筒运动、螺杆静止，则使用准静态假设，根据流道形状变化的周期性，绘出一系列相差一定角度的流道来代表一个旋转周期，并分别计算每一几何体。后来Ployflow软件研发了网络叠加技术(Mesh superposition technique)，模拟了螺杆转动、机筒静止的真实情形，与使用准静态假设相比，大大减少了网格处理的工作量、机时和计算误差。图9.1.2为Polyflow软件双螺杆流计算域。图9.1.2(a)给出双螺杆元件横截面选取的参考位置。图9.1.2(b)给出流道网格划分和边界条件。该图显示双螺杆计算域流道入口和出口边界条件可给定流量或压强，假设螺杆表面和机筒内壁无滑移。

图9.1.2 Polyflow软件双螺杆计算域

(a)双螺杆元件横截面选取的参考位置(b)流道网格划分和边界条件

2001年，彭炯和陈晋南^[22]在国内首次使用网格叠合技术，数值模拟同向旋转双螺杆挤出机计量段聚合物挤出的过程，用Carreau和近似Arrhenius公式的模型描述熔体的流变特性，数值计算计量段的三维非等温流场，分析熔体速度、温度、压力、黏度、黏性耗散热的分布，分析了螺杆转速、轴向压差对挤出量的影响。

在聚合物工程挤出过程中，壁面存在滑移，否则将出现物料堆积、滞流、烧焦等问题。实验研究不易研究壁面滑移的问题。2004年，Hu和Chen^[23]首次引入Navier slip law定义壁面有滑移边界条件，用Carreau模型模拟双螺杆挤出螺纹元件的三维等温流场。对于不同的系数，计算了螺旋通道的等速度曲线和相互啮合区域的剪切速率分布，分析讨论不同壁面滑移系数的轴压差、平均剪切速率和分散混合指数。近年来，在壁面滑移条件下，研究聚合物螺杆的三维非等温非牛顿流体的流动日见增多。

由于不能模拟整个螺杆，数值模拟双螺杆挤出聚合物的流场，流道进出口边界条件的设置一直是一个颇具争议的问题。由于事先无法获得计算域进出口平面上的真实边界条件，在数值模拟聚合物螺杆挤出过程时，大都采用放松边界条件。为了考察放松边界条件数值模拟结果的影响。2005年，在流量恒定的条件下和进出口给定三种不同分布形式的速度边界条件下，胡冬冬和陈晋南^[24]用Carreau模型数值模拟双螺杆挤出流道。数值计算结果表明，在体积流量恒定的条件下，流道进出口不同分布形式的速度边界条件对流场的影响主要集中在进出口附近区域。但是，对离进出口边界较远的流场影响很小。一般而言，当计算域所对应的螺杆较长时，可以忽略流道进出口的放松边界条件所引起的误差。当计算域较短时，不宜直接采用放松边界条件，应在计算域进出口增加适当长度的流体流动发展段。考虑边界效应的影响，不要取进出口边界计算值分析讨论计算结果。

商业软件提供了各种网格划分的方式，可以根据研究问题的复杂性和计算内存，选取网格划分的方式。例如，用正四面体网格划分形状不规则的螺杆和螺筒，用正六面体网格划分形状规则的流体区域。先分别生成螺杆和螺筒的网格，然后通过Polyflow软件中的网格叠加技术，将螺杆和螺筒流体区域的网格组合，生成真实流道的网格，如图9.1.2 (b)所示。

(3)数值模拟的迭代方法和计算精度

商业成熟的软件包括了不同的插值函数、计算迭代方法和计算精度。使用数值计算软件时，一定要选择合理的迭代方法和计算精度。例如，使用Polyflow软件数值求解非线性耦合方程组式(9.1.1)至式(9.1.7)时，数值研究聚合物螺杆挤出过程的计算中，速度采用mini-element插值，压力采用线性插值，黏度采用Picard迭代。将方程式(9.1.1)至式(9.1.7)离散，用隐式欧拉法联立求解离散化的方程。若选择计算精度太高，由于被研究聚合物流变性能和设备结构问题的复杂性，计算机的内存不够，计算将不会运行或中途终止。选择的计算精度过低，得到的结果不好，无法分析流场的物理量。考虑到流道结构复杂，计算周期长，迭代误差大，一般选择计算精度为10^－3，略高于工程允许的误差范围。从数值模拟与实验比较的结果来看，在误差允许的范围内，绝大多数模拟结果与实验结果是一致的，从而有力地证实了利用CFD及其软件包，数值研究聚合物加工成型的可靠性和先进性。

图9.1.3给出数值模拟聚合物螺杆挤出加工过程的示意图。图9.1.3中左方框是输入的物理量，包括螺杆流道几何结构、实验测试确定的物性参数、边界条件和工艺条件，以螺杆挤出为例，输入转速、温度、压力或流量等；使用CFD软件数值求解非线性的控制方程，可得到图9.1.3中右方框的输出物理量，包括速度场、压力场、剪切应力场、剪切速率场、黏性热场、黏度场和温度场。可模拟物料粒子的运动轨迹，模拟双螺杆挤出中物料动态混合过程，得到应变分布函数SDF、物料停留时间分布函数RTD。试验测试流量、压力、温度、扭矩和轴功率等特性参数。用流变学的理论分析试验测试数据和数值计算的结果，分析聚合物挤出加工过程，深入研究聚合物加工成型的机理。

图9.1.3 数值模拟聚合物螺杆挤出加工过程的示意图

下面介绍数值模拟研究工程问题的基本步骤和方法：

第1步 根据研究的问题，用物理准数选用成熟可靠的商业软件，例如低雷诺数高黏性聚合物流体的流动选择Polyflow软件；或开发相应的计算机程序，根据研究问题的需要，编制部分软件与通用软件接口使用。

第2步 根据实际工程问题，在软件的前处理器中建立研究对象的物理模型，选取合适的坐标系，画出研究对象结构图。选取网格划分的方式，先分别生成螺杆和螺筒的网格，然后用软件网格叠加技术，组合螺杆和螺筒流体区域的网格，生成流道计算网格。

第3步 实验测试物料的流变性能，使用软件和实验测试材料流变数据，确定材料本构方程的参数。

第4步 建立研究对象的数学物理模型，由实验测试的数据和工艺条件，确定相应的边界条件和初始条件。

第5步 选择适当的数学计算方法和计算精度，数值求解数学物理模型，应用软件处理数值计算结果，确定流场特殊点的物理数值，根据分析问题的需要，画出速度场、压力场、剪切应力场、剪切速率场、黏性热场、黏度场和温度场，以及粒子动态混合过程，画出应变分布函数SDF、物料停留时间分布函数RTD的曲线。

第6步 将数值近似解与实验测试结果比较，分析所求数值近似解的精确性和可靠性，必要时修正数学模型，重复上面的第3步至第5步。

第7步 最后，理论上深入分析解释数值近似解的物理意义，分析研究聚合物材料加工成型的机理，从理论和技术上指导生产本质安全过程的设计，优化设备结构、工艺条件和试验方案，指导工程开发过程。

早期，陈晋南课题组师生使用软件数值模拟聚合物加工成型过程，在研究工作中，师生曾遇到不少问题走过弯路，不断总结经验成长。留学回国以来，陈晋南曾担任国家自然科学基金的面上项目和青年基金项目评审邀请（有机聚合物材料学科）的通讯评审专家，有幸学习审核了不少申请报告，审核了不少国内核心期刊有关数值模拟的论文，学习了不少好文章，也学习了解国内研究情况，也发现一些共性的问题。这里分析容易出现的问题：

① 物料流变性能确定的错误。发生这种情况有几种可能，使用单一流变仪测试物料的性能，没有测试低剪切速率和高剪切速率的物料的流变性能，或测试数据太少，仅得到线性的流变本构方程；或随便从软件的数据库，随意选择数学模型和本构方程，描述自己研究的问题；或认真测试了物料的流变数据，但是没有修正处理测试的实验数据，直接把测试的物料表观黏度当物料黏度使用，计算误差就会大一些。当时国内不具备测试特殊材料的设备和修正的条件，陈晋南课题组也曾使用表观黏度数值计算研究问题，相对分析讨论问题。早期，国内有的流变仪处理流变数据的软件也没有考虑表观黏度的修正问题。由于物料流变性能测试数据有问题，最终导致数值模拟的结果误差大，或者是错误的。

② 控制方程和边界条件的错误选择。研究对象搞错了或选择不合理，把非等温场处理成等温场。没有选择计算精度，有的没有艺条件和边界条件，就有了计算结果。

③ 数值模拟结果的分析错误。由于数学物理基础知识不够，无法应用聚合物流变学分析数值模拟的结果，没有与实验研究分析对照，错误地分析了数值模拟的结果，无法指导工程实际。

数值计算已与理论分析、实验被并列公认为当代科学研究的3种手段之一。这3种方法有机结合，才能推动聚合物材料加工成型新技术、新设备、新材料的发展。提高使用数值计算的水平是行业发展和创新的需要。

下面的9.2节至9.5节介绍陈晋南课题组使用Polyflow软件研究聚合物加工成型过程的典型工作^[11-90]，包括聚合物螺杆挤出加工成型过程的数值模拟、聚合物模具挤出成型过程的数值模拟、聚合物挤出注塑成型过程和聚合物挤出吹塑成型过程的数值模拟。