聚合物流变主曲线探析

每种流变仪的测量系统都可以覆盖一个相应的时间跨度，频率范围很少能超出3个数量，即ω＝0.01～10s^－1，技术上规定最小和最大值通常为ω＝0.001s^－1和ω＝100s^－1。影响测量范围下限值的原因是，每种流变仪设定了有效最小应力值能产生被检测的最小变形。另外，实际流变测量的局限性来源于实验时间超长，长到基本实验不能承受的地步。还有一种局限性，在低温下样品非常黏，用现有流变仪不能测试其黏度。Schramm^[2,3]举例分析了这一情况。测试低剪切速率10^－4s^－1胶状糊填料对材料流变性能的影响，实验要等待3h。若需要ω＝10^－5s^－1的数据，则要等待24h才能得到第一个测试点的数据，要得到完整的G′、G″对频率的曲线，至少不能少于两天。

这样长的测试时间是不切实际的。由于聚合物的流变性对温度和剪切速率都很敏感，因此要表征一种聚合物的流变行为就需要大量的数据，所以有必要寻找一种有效的方法。只需通过少量实验数据就能预计聚合物的流变性质。同时还能比较各种聚合物的流变行为。为了实现这一点，就需绘制流变主曲线^[2-3]。

本小节介绍绘制流变主曲线的方法，包括WLF时间—温度等效原理、流变主曲线的绘制2部分。

这里介绍WLF时间—温度等效原理(Time-temperature equivalence principle)。当对材料施加正弦波方式施加剪切应力，黏弹性流体的力学响应与该材料的分子体积元的可移动性有关。用松弛时间谱图来表征这种移动性。材料的流动性与流体的主要成分种类和含量百分比有关，也与材料所有其他混合成分的种类有关。低温下材料的可移动性下，这类液体的响应缓慢。若提高温度，增加了分子的移动性，可以提高黏弹性流体的响应速度，从而可以研究热塑性熔体被包围的填料聚集体或类似橡胶的体积元的作用。可见，流变测试样品的温度与响应时间（测试视频）之间存在很强的表征流体特征的相关性。

早在1955年，Williams，Landel和Ferry等人研究了这一相关性，推导了一个数学公式——WLF方程来描述之一相关性，即时间—温度叠加原理。时间温度叠加原理以这三位科学家名字的头一个字母命名。WLF方程的理论基础是流体物理结构对温度的依赖性。他们用理论支持了经验的曲线位移的方法。

从聚合物的变形—温度曲线可知，改变温度，可使同一聚合物从一种力学状态过渡到另一种力学状态。从聚合物的黏弹性中也知道，改变力的作用速率，也可使聚合物的力学性质发生改变。那么，温度和力的作用速率这两个因素的效果是否相当？在恒定外力作用下，观察在不同温度下聚合物的变形值，如图8.4.12中所示。由图中看出，变形总值与温度的变化关系不大。温度变化只影响它们的变形速率。如果把同样的数据改绘成不同作用时间下变形与温度的关系，详见图8.4.13，可以清楚看出，不同温度和作用时间的组合，都可以达到同一变形值。如图8.4.13中所示，虚线ABC标出的同一变形，可在作用时间t₁和温度T_A时得到，也可以在作用时间t₂和温度T_B得到，或作用时间t₃和温度T_C得到。

换言之，在高温度下和较短时间得到材料的同一变形，也可在较低温度下和较长时间得到。就是说作用时间和温度这两个因素对变形有着等效的影响。这个重要的结论，就是所谓的时温等效原理。

根据这个原理，难以用实验测定的作用时间非常短的载荷，可以用降低温度的方法来模拟，作用时间长的载荷，可以用升高温度的方法来模拟。这样就可以利用现有实验手段获得力的作用时间范围比较宽的实验数据。运用这一叠加原理，可以减少实验次数，避免在不合适的条件下做流变测试实验。应用时温等效原理，用有限的实验测试数据绘制流变主曲线，进而研究材料的流变性能。

图8.4.12 在恒应力作用下，不同温度时变形与时间的关系

图8.4.13 在恒应力作用下，不同作用时间时变形与温度的关系

由于聚合物的流变性质与温度和时间这两个因素密切相关。所以，表征聚合物的流变性质时，应严格规定温度和时间。例如，要全面反映聚合物的流变性质，应该在聚合物的使用温度范围内各种温度下，以不同的剪切速率测定的结果来表征。但是，这种方法太繁琐，如果选择5个实验温度和5种剪切速率，结果可得出25条曲线。如果把温度和剪切速率的范围划分得更小一些，就会有更多的曲线，而且还不能很全面地反映聚合物的流变性质。

为了简单而全面地反映聚合物地流变性质，根据时温等效原理提出了一个时间—温度换算的处理方法，用来反映聚合物地流变情况。利用时间—温度转化因子，将不同温度和作用力速率下所得到的数据转换成一条曲线，把这条曲线称为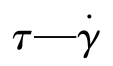“主曲线”，或称“组合曲线”“总曲线”“换算曲线”。

图8.4.14给出低密度聚乙烯在各种不同温度下的一组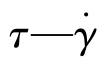曲线。要将其绘制成为主曲线，根据时间等效原理，首先选定一参考温度曲线，然后将其他曲线向参考温度曲线方向平行移动，使它们叠加到参考温度曲线上去。(www.xing528.com)

将高于参考温度的曲线向左边移动，低于参考温度的曲线向右边移动。经这样叠加后就可得到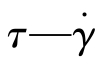主曲线，详见图8.4.15。重要的是要知道每条曲线必须移动多少量才能叠加到参考温度曲线上去，以及曲线的移动量与温度有何关系？沿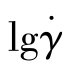坐标轴的移动量α_T叫移动因子。移动因子为10时，意味着曲线沿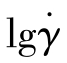坐标轴平移了一个数量级；当移动因子为100时，意味着曲线沿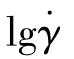坐标轴平移了两个数量级。

图8.4.14 不同温度低密度聚乙烯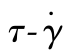曲线^[14]

图8.4.15 200℃的LDPE主曲线^[14]

α_T的数字表达式为

式中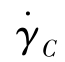，为参考温度曲线上的一定剪应力所对应的剪切速率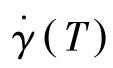；为温度T时，与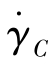对应着同一剪切应力的剪切速率。

可以证明，移动因子也可表示为

式中，η_C(T)为参考温度曲线上的一定剪应力所对应的黏度；η(T)为温度T时与η_C(T)对应着同一剪应力的黏度。

流变主曲线得出后，就可以利用流变主曲线估算任意温度下的流变行为。在缺少数据的情况下，可以估算分子不同、结构相似的聚合物流变行为，有了各种聚合物的主曲线，就可比较各种聚合物的流变行为。由此可知，主曲线对研究聚合物的流变行为是十分方便的。

用WLF时温叠加法能研究宽范围流体的流变性。但是，一定要记住，在整个温度范围内测得的曲线只能随着温度逐渐变化，即材料的流变行为不能突变。例如，在接近玻璃化转化温度T_g时，材料分子流动急剧变化，不能将玻璃化转化温度T_g以下的温度曲线外推至T_g以上的温度。这样是没有任何意义的。另外还要注意，若混合物中高百分比填充物与基质物料差异很大，应该严格检验测得的位移因子。当讨论主曲线时，不可忽略的事实是，在扩展范围的边界处，数学近似结果比实际测量数据有所降低。

这里没有介绍详细绘制主曲线的步骤，有兴趣的读者可以参看有关文献^[2,3]。

本章仅介绍几种常用流变仪的工作原理，读者有兴趣或工作的需要，可深入学习专门流变学测量和相关仪器的书籍和参考文献。