完全发展区流场分析

在毛细管的完全发展区，在柱塞压力下，物料做充分发展等温稳定的轴向层流，即做测黏流动。本小节重点分析毛细管中完全发展区熔体的流场，深入讨论恒速型毛细管流变仪的测量原理^[2-6]，包括剪切应力的计算、Weissenberg-Rabinowtsich剪切速率公式、Ostwald-de Waele幂律方程3部分。

设毛细管半径为R，完全发展区长度为L′。在柱塞压力下，不可压缩的黏弹性流体作等温稳定的轴向层流。因为毛细管是圆柱型的，所以选取柱坐标系r，θ，z分析物料的流动行为，见图8.2.3。可以看出，流速方向（1方向）在z方向，速度梯度方向（2方向）在r方向，θ方向（3方向）为中性方向。

该流体流动与6.1.2节长圆管流道流体的压力流相同。根据分析流动的特点，不可压缩黏弹性流体的等温稳定层流，可以忽略质量力和惯性力；流速只有u_z分量不等于零，速度梯度分量仅有∂u_r/∂r不等于零，偏应力张量可能存在的分量有τ_zr，τ_zz，τ_rr，τ_θθ。于是得到连续性方程为

图8.2.3 流动完全发展区结构示意

简化柱坐标系的运动方程式(3.2.28b)，可分别写出3个坐标方向运动方程

r方向

θ方向

z方向

在毛细管流道中，由于熔体或流体的黏性，最贴近管壁的一层流体是紧贴着管壁不流动的。可假定毛细管壁面无滑移，有边界条件

由于物料流速较高，通过毛细管的时间很短，可以忽略与外界的热量交换，熔体等温流动，不考虑能量方程。

分析运动方程的各式，式(2)含法向应力分量，主要描述材料的弹性行为；式(3)显示法向应力不是θ的函数，因此τ_θθ＝0；式(4)含有一个剪切应力分量，主要描述材料黏性行为。设沿z轴方向的压力梯度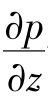恒定不变，可以直接积分式(4)，得到毛细管内的剪切应力分布为

由此求出管轴心处和管壁处的剪切应力分别为

由上式可见，在毛细管内物料流动时，同一横截面内各点的剪切应力分布并不均匀。轴心处剪切应力为零，而管壁处取最大值τ_w。可以看出，只要毛细管内的压力梯度确定，管内任一点的剪切应力也随之确定。这样，一个测剪切应力的问题被归结为测压力梯度的问题，而后者是较易测定的，只要测出毛细管两端的压力差除以毛细管长度即可，得到管壁处最大剪切应力的简单公式

式中，Δp是管长L的压力降。

毛细管中任一点的剪切应力为

1851年，Stockes导出公式(8.2.3)，该式称为Stockes关系。在一定压力梯度 Δp/L下，剪切应力同离开轴的距离成正比，且与流体性质无关。对任何一种流体，无论是牛顿型流体还是非牛顿型流体均成立。计算过程中并不涉及流体的类型。

剪切速率的测量和计算不像剪切应力那样简单，它与流过毛细管的物料种类有关。首先讨论牛顿型流体的简单情形，第6章详细推导了长圆管流道流体流动，得到速度分布式(6.1.25)和体积流量式(6.1.26)，分别为

可见，速度曲线是一个抛物线。在管轴心处，物料流速最大，管壁处物料流速为零。由流量式得到

将式(8)代入式(8.2.2)，得到管壁的剪切应力为

由式(8.2.4)确定在毛细管壁处牛顿型流体所承受的剪切速率

式中，D为毛细管直径；u_Zb为物料流经毛细管的平均流速。

式(8.2.5)的物理意义是只要测量体积流量q_V或平均流速u_Zb，则可直接求出牛顿型流体在毛细管壁处的剪切速率。这里再强调一下，式(8.2.5)求得在毛细管管壁处牛顿型流体的剪切速率，它与式(8.2.2)求得的管壁处的剪切应力相对应。必须对同一流体元测量剪切应力和剪切速率，计算出的黏度才能反映真正的物料性能。

不指明流体的具体类型，对于非牛顿流体黏度为η，剪切速率的计算比较复杂^[4]。实验中通常测量体积流量q_V，需要计算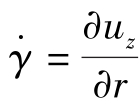。q_V与速度有直接关系，对速度体积分，运用管壁无滑移边界条件u_z|_r＝R＝0，得体积流量为

由式(8.2.2)和式(8.2.3)，有(www.xing528.com)

将式(2)的r和dr代入式(1)，作变量替换，得到

积分上式，得到

由式(4)得到

由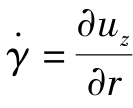，得到

将式(8.2.5)的管壁处牛顿型流体的剪切速率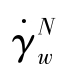记为表观剪切速率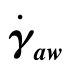，计算流量

再将式(7)代入式(6)，得到重要的Weissenberg-Rabinowtsich公式

此式用于计算非牛顿型流体流经毛细管时，毛细管管壁处物料承受的真实剪切速率。

综上所述，用毛细管流变仪测量物料黏度的步骤和计算方法如下：

① 首先把流经毛细管的任何流体均视为牛顿型流体，通过测量完全发展流动区上的压力降计算管壁处物料所受的剪切应力τ_w，测量其体积流量q_V或平均流速u_Zb，按式(8.2.5)求出管壁处的管壁处表观剪切速率；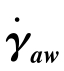

② 根据具体物料的性质，即管壁的剪切应力τ_w与表观剪切速率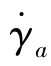之间的本构依赖关系或测量得到的的关系曲线，由式(8.2.6)求出该物料流经毛细管时在管壁处的真实剪切速率；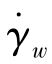

③ 由管壁的剪切应力τ_w和剪切速率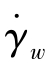得此计算物料的黏度。

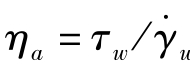对于若干聚合物熔体的加工过程的剪切速率范围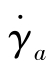＝(10¹~10³)s^－1内，由体积流量按式(8.2.5)确定，用幂律本构关系式(5.2.18)，确定管壁切向应力与剪切速率的近似关系，为

将其代入公式(8.2.6)，得到

将其代回幂律流体的本构关系式(5.2.18)，得到

式中，K为流体的稠度系数，当n＝1时，为牛顿流体，稠度系数等于黏度系数，K＝η。

式(8.2.8)称为Ostwald-de Waele幂律方程。作为描述物料非牛顿流动性的最简单的近似，该方程具有简单的形式，广泛地使用于近似分析问题。该方程是经验性的，缺点是物理意义不明确，适用的剪切速率范围较窄。

例题8.2.1 在毛细管内，黏性幂律流体的速度分布不同于牛顿流体。确定毛细管内幂律流体的速度分布。

解：根据毛细管内熔体流动的规律u_r＝0，简化柱坐标系变形速率张量分量式(3.1.47)中的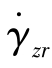，有

积分上式，得到

对于幂律流体，任一点变形速率为

将其代入式(2)积分，得到毛细管内幂律流体的流速分布公式

式中，平均速度为u_zb＝q_V/πR²。

当n＝1，式(8.2.9)还原为牛顿流体公式。在第6章曾经分析过长圆管内流体的速度分布。由图6.1.9可见，当n<1，流体呈假塑性时，管内流体的流速分布曲面比牛顿型流体的抛物面扁平些，呈柱塞状。当n>1，流体呈胀流性时，流速分布曲面呈前突形。