实验测定单轴拉伸黏度的方法

本小节介绍单轴拉伸黏度的实验^[10,12]，包括恒拉伸速率实验法、等温纺丝实验法。

拉伸流动测试装置(extensional flow rheometer)如图7.4.7所示。仪器的工作范围为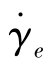＝5×10^－3~5s^－1、负荷0~2kg。在实验中，将长L＝21.5cm单丝两端夹紧，置于硅油浴槽内，卷绕罗拉以恒速U₀转动，长丝受力，另一端的仪器instron记录测试的结果。单丝运动过程中，由于单丝置于硅油浴槽内，单丝没有受到剪切应力。在整个单丝的拉伸成型过程中，一个材料元所受的拉伸速率等于常数。

若设夹持的丝条长度为L，罗拉卷以恒速U₀转动。丝条某一截面开始在位置为L₀，速度为U₀，经过时间t后，则为L(t)和u(t)。按照拉伸速率的定义，有

图7.4.7 拉伸流动实验装置^[10]

丝元长度随时间的变化规律为

丝元的速度为

实际上，在熔体纺丝过程中，尽管纺丝工艺过程是稳定的。一个材料元所经历的拉伸速率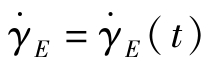自上而下时刻变化，单轴拉伸流动是非稳定的流动。显然，实际拉伸中丝条长度未必一定按式(7.4.6)规定的e指数规律变化。材料元长度随时间的变化规律应记为

设z方向为拉伸方向。因此，欲了解丝长的变化规律，必须知道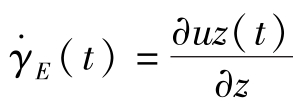的具体函数形式。

定义表观拉伸黏度 实际纺丝过程即非稳态拉伸流动中的拉伸黏度称为表观拉伸黏度。表观拉伸黏度计算式为

其中

F_T(z)＝F_L+F_G+F_D+F_I

式中，F_T(z)为丝条在z方向（第一方向）变形所受的总张力；可从力平衡方程求得：F_L为卷线装置处（在z＝L处）的实测张力；F_G为质量力；F_D为摩擦阻力；F_I为惯性力；A(z)和du_z(z)/dz分别为纤维在z处的横截面积和轴向速度梯度。

这里没有展开讨论，读者可参看有关恒拉伸速率实验法的文献。

恒速率实验装置所测拉伸速率范围较小，测试的数据与实际情况差别也比较大。考虑到丝条冷却会使熔体拉伸黏度增加，其变化规律服从Eyring-Frenkel关系式

式中，E为黏流活化能；α₀为材料常数。

为了改进实验测试的方法，Han和Acierno等相继研究了等温纺丝法，在喷丝口外设置一个等温室，以减少温度变化对纺丝过程的影响。下面介绍等温熔体纺丝法实测表观拉伸黏度。

实验装置如图7.4.8所示。喷丝头部分用单孔纺丝机或毛细管流变仪代用。喷丝板下设长为15~20cm带有摄像机的保温夹套。摄像机可拍摄喷丝板下等温夹套内熔体丝直径的变化情况。导丝盘后的张力仪测定卷绕的张力。实验条件可模拟纺丝条件。控制等温夹套和纺丝熔体温度相同，熔体以一定体积流量通过直径D的喷丝孔，丝条出喷丝孔经等温夹套后冷却，最后以一定的卷绕速度u_L卷绕的筒上。

分析式(7.4.9)可知，式中除F_L为实测张力外，其他F_G、F_D、F_I的确定均需要知道纤维直径或纤维轴向速度。另外，式(7.4.9)中面积A(z)的确定也需要确定纤维直径的轴向分布。为此首先求出纤维直径沿轴向的变化规律d(z)是十分重要的。用摄影方法拍照稳定流动的丝条，从照片量取纤维直径沿轴向变化的数据d(z)。由此可进一步计算A(z)，并通过流量求出u_z(z)(www.xing528.com)

图7.4.8 等温纺丝实验装置示意^[10]

式中，q_V、q_m分别为熔体体积流量和质量流量；ρ为熔体密度，在等温下为定值。

用公式(7.4.11)做u_z(z)－z的图，由图中可求出斜率du_z(z)/dz的变化规律。于是，A(z)、du_z(z)/dz、F_G、F_D、F_I均可确定，进而计算物料的表观拉伸黏度η_Ea。

用公式(7.4.11)做u_z(z)－z的图，由图中可求出斜率du_z(z)/dz的变化规律。于是，A(z)、du_z(z)/dz、F_G、F_D、F_I均可确定，进而计算物料的表观拉伸黏度η_Ea。

在不同纺丝条件下，做实验，用上述方法绘制流变图。图7.4.9给出不同拉伸比聚丙烯纤维直径和速度沿z方向变化。图7.4.10给出不同拉伸比低密度聚乙烯纤维直径和速度沿z方向的变化。图7.4.11给出不同拉伸比聚丙烯拉伸速率沿z方向变化。可看到，在熔体纺丝过程中，一个材料元历经z轴各处的拉伸速率不是常数。

图7.4.9 不同拉伸比聚丙烯的纤维直径和速度沿z方向的变化^[11]

注：纺丝条件t＝180℃，q_m＝1.606g/min，U₀＝2.78m/min。

在纺丝条件下，q_m＝0.0455g/s，U₀＝2.17cm/s，u_L/U₀＝501.78，t₀＝220℃，计算非等温聚苯乙烯丝条上各个力沿z方向的变化。表7.4.1给出非等温纺丝中聚苯乙烯丝条上的力沿z方向的变化。可以看到，质量力F_G的贡献沿纺丝线远离喷丝口迅速减小，而阻力F_D、惯性力F_I和总的变形力F_R则沿着纺丝线增加。这与工业中的实际情况相符。

图7.4.10 不同拉伸比低密度聚乙烯纤维直径和速度沿z方向的变化^[11]

注：纺丝条件t＝200℃，q_m＝1.481g/min，U₀＝2.627m/min。

图7.4.11 不同拉伸比聚丙烯的拉伸速率沿z方向的变化^[11]

注：纺丝条件t＝180℃，q_m＝1.606g/min，U₀＝2.78m/min。

表7.4.1 非等温纺丝中聚苯乙烯丝条上的力分布^[7]

注：gf＝9.8×10^－3N。

图7.4.12 4种不同聚合物熔体的表观拉伸黏度η_Ea随拉伸速率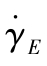的变化^[11]

图7.4.12给出4种不同聚合物熔体的表观拉伸黏度η_Ea随拉伸速率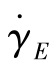的变化。由图可知，高密度聚乙烯、聚苯乙烯和聚丙烯的表观拉伸黏度η_Ea随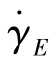增大而减小，而低密度聚乙烯在所研究的范围内表观拉伸黏度η_Ea保持为常数。图7.4.12所示的拉伸黏度的变化规律与图7.4.13所示的规律不一致。图7.4.13给出的是物料稳态单轴拉伸的拉伸黏度，而本处为非稳态单轴拉伸的表观拉伸黏度，两者不存在可比性。