辊筒缝隙中黏性流体的流动优化

聚合物材料压延成型过程一定与温度有关，为了简化问题，本小节分析对称辊筒等温加工成型过程，求解两辊筒间隙物料的等温流场，分析流场的压力和速度的分布^[2]，包括控制方程的简化和求解、辊筒缝隙物料的压力分布、辊筒缝隙物料的速度分布和功率3部分。

在两辊筒间隙中，取直角坐标系如图7.3.3所示，坐标原点在两辊筒最小间距的中心。两辊筒半径相等R₁＝R₂＝R，辊距为2H₀，R≫H₀；辊筒表面线速度相同u₁＝u₂＝u。因为熔体的流动以x对称，图7.3.1仅给上半平面一个辊筒缝隙流场的示意图。由此图可见，x方向为物料主要流动方向，y方向为两辊筒轴心连线方向，z方向垂直于纸面向外。辊筒表面各点的纵坐标y＝h(x)可表示成x的函数，该函数形式与辊筒形状有关。

图7.3.3 压延机对称辊筒间隙坐标和尺寸^[9]

根据压延成型过程熔体流动特点，分析辊筒系统和物料特性，做出简化假设：

① 物料为不可压缩牛顿性流体▽·u＝0，牛顿型流体黏度μ和密度ρ均为常数，且牛顿流体有黏性而无弹性，因此应力张量中法向应力分量等于零τ_xx＝τ_yy＝τ_zz＝0；

② 辊筒加工成型过程为对称性过程，在x-y平面上，物料自左向右流动，流动主要方向在x方向，有u_x≫u_y，即y方向速度近似等于零，有u_y≈0，且；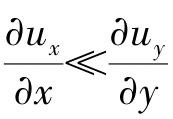

③ 辊筒间隙物料的流动为稳定等温流动，有∂/∂t＝0和u≠u(T)；

⑤ 在壁面上，熔融物料无滑移运动，即最贴近辊筒壁的一层熔体是随辊筒一起运动的；

⑥ 由于物料黏性大，黏性力极大的大于质量力和惯性力，忽略质量力和惯性力。

这种简化假定称作润滑近似假定(lubrication approximation)，根据以上假设条件，简化描述辊筒缝隙黏性流体运动的控制方程。由于辊隙中物料的流动为不可压缩流体的一维稳定流动，故连续性方程为

简化运动方程(3.2.19b)，得到x，y方向的方程分别为

边界条件：①u_x[y＝±h(x)]≈U₀，②u_y[y＝±h(x)]≈0，③＝0

方程(1)~(3)构成牛顿型流体流经两辊间隙的定解问题，可看出压力仅是x的函数，即p＝p(x)。式(2)转化为方程

将式(7.3.1)积分两次，用所有的边界条件①，② 和③确定积分常数，得到牛顿型流体流经两辊筒间隙流道内的速度分布

分析上式可知，u_x速度分量不仅是坐标y的函数，也是x的函数，u_x＝f(x，y)。但是，u_x对x的函数关系隐含在h＝h(x)和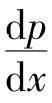之中。h＝h(x)可以根据辊筒曲面的形状函数加以确定，而压力梯度尚未知。下面确定辊筒缝隙物料的压力分布。

欲求压力梯度，需先求出单位宽度体积流量q_V。将速度体积分，确定流量为

用体积流量表示压力梯度，有

由上式可见，压力梯度仅为x的函数，隐含在h(x)中，函数关系不够明确。由图7.3.4给出的几何关系，进行变量替换，令

在R≫x的流道内，展开式(1)中的(R²－x²)^1/2，有

图7.3.4h与H₀的几何关系

将式(2)代入式(1)，有

最方便的做法是定义量纲为1变量，量纲为1坐标x′(0，1)、y′(0，1)分别为

量纲为1的速度和压力分别为

得到

将h(x)的表达式代入式(7.3.4)中，得到压力梯度公式的显式形式

其中引入一个量纲1参数λ为

λ是非常重要的一个参数。压力梯度用λ值表示出来了。设物料出料脱辊处的辊距为2H，即压出的料片厚度为2H。脱辊处物料的流速等于辊筒表面线速度U₀，因此流量q_V＝2U₀H，代入式(7.3.7)得量纲为1离辊距离

由上式，只需测出料片厚度2H，即可求出λ的参数值。

积分式(7.3.6)，得辊筒间的压力分布公式

其中，

式中，系数为压力基本常数；C(λ)为积分常数。

由边界条件x′＝λ，p＝p₀＝0，确定积分常数为

由以上分析可知，压力分布p为坐标x′与参数λ的函数，可记为

压力基本常数标志着辊筒内物料承受压力的数量级。在分离点后，速度分布是均匀的。均匀流速分布对应于du_x/dy＝0，d²u_x/dy²＝0。由式(7.3.1)可知，在分离点处，压力梯度为零。当量纲为坐标x′＝±λ时，dp/dx′＝0，即为两辊筒缝隙物料压力取极值的位置。压力具有3个特征值，而对应的3个压力值分别为(www.xing528.com)

① 当x′＝+λ时，p(－λ，λ)＝0

② 当x′＝－λ时，

③ 当x′＝－∞时，p(－∞，λ)＝0

也可以计算量纲为1压力梯度，讨论量纲为1压力梯度的极值位置。

由式(7.3.13)求极限，得超越方程为

解此方程得到λ₀＝0.475，由公式(7.3.8)得到

由此式可知，对于理想情况片材厚度只与λ₀有关。

将λ₀＝0.475代入(7.3.11)，计算得C(0.475)＝0.504，从而使最大压力计算简化为

(1)物料速度的分布

为确定辊筒缝隙物料的速度分布，将式(7.3.5)和压力梯度式(7.3.6)代入速度式(7.3.2)，并用量纲为1变量x′代换x，得到量纲为1的速度分布式

用h(x)代替H₀无量纲为1化y，令ζ＝y/h(x)代上式，得到

为了确定环流区的位置，令ζ＝y/h(x)＝0和无量纲速度式(7.3.17)等于零，有

将式(7.3.14)代入上式，确定流动驻点的位置为x′^∗≈－1.64。就是说，在x′^∗<－1.64的区域沿着轴线存在倒流，形成一种回流；由于压力的存在，在x′<－λ区域倒流分量叠加在拖曳流动分量上，如图7.3.5所示。

图7.3.5 两辊筒缝隙流道物料速度分布

由图7.3.5可知，图中有两个特殊点，在x′＝±λ处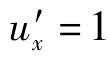，，即u_x＝U₀。将x′＝±λ代入式(7.3.17)可证明。

(2)辊筒的驱动功率

因为在面积元ds＝bdx上的功为dP＝U₀τ(x，y)bdx。所以，分布于整个压延宽度的功率必为一个积分

对于牛顿型流体，有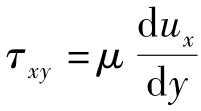，对速度公式(7.3.2)求导，得到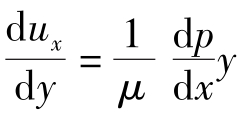，用压力梯度(7.3.6)计算剪切应力，得到

将和式(7.3.19)代入式(7.3.18)，得到

积分上式，得到

其中

对于理想情况，λ₀＝0.475，M(0.475)＝1.08，故有

例题7.3.1^[11]已知某压延机辊筒半径R＝0.1524m，压延宽度b＝1.8288m，H₀＝0.00635m，压延材料的表观黏度μ＝10³Pa·s，线速度U₀＝0.1016m/s，试计算：

① 薄板成型厚度H；

② 最大压力p_max；

③ 辊筒的驱动功率P。

解：首先从式(7.3.14)计算出

H＝1.226H₀＝1.2260.00635＝7.78510^－3(m)

然后按公式(7.3.15)计算最大压力

最后，按公式(7.3.21)算辊筒的驱动功率为

为了简化问题，本节仅分析牛顿流体等温压延成型过程。实际上，压延成型过程不能忽略温度的影响。Tadmor和Gogos详细分析了非等温辊筒缝隙流道黏性流体的流动，例如活性注塑(化学反应Reactive injection molding)和压缩(Compression molding)等成型过程，讨论了温度对物料流动的流场物理量的影响，感兴趣的读者可以学习专著^[1,9]。