流体非稳态流动的斯托克斯问题优化

偏微分控制方程也常用积分变换的方法求解。积分变换是通过积分将某一个函数类中的函数变换为另一个函数类中的函数的方法。积分变换是一种求解微分方程特殊的“运算方法”，可将线性常微分方程经过变换转化为代数方程，将偏微分方程变换后得到降阶或同价的常微分方程，从而使运算简便许多。常用拉普拉斯变换法求解非稳态流体流动的控制方程。

斯托克斯两个问题的解是黏性流体力学非稳态流动的两个精确解^{[1，2，5，7]}。本小节分别介绍用拉普拉斯变换求解流体非稳态的流动，包括积分变换、斯托克斯第一问题、斯托克斯第二问题3部分。

为了求解流体非稳态流动的斯托克斯问题，首先介绍积分变换的基础知识^[13]。

定义：如下含参变量s形式的积分

称为积分变换。式中，K(s，x)称为积分变换的核函数，它是s和x的已知函数；F(s)称为原函数(或象原函数)f(x)的象函数；若a和b为有限值，则式(6.4.2)称为有限积分变换，一般情况下，f(x)和F(s)是一一对应的。

这里仅简单介绍使用比较多傅里叶变换和拉普拉斯变换。

(1)傅里叶变换

定义 若f(t)在(－∞，+∞)区间上，满足有限区间上满足狄利克雷条件，在无限区间(－∞，+∞)上绝对可积，在f(t)的连续点处，有

令

则有

式(6.4.3a)称为函数f(t)的傅里叶变换式，函数G(ω)称为f(t)的傅里叶变换，式(6.4.3b)称为G(ω)的傅里叶逆变换。G(ω)为f(t)的象函数，f(t)为G(ω)的象原函数。因此象函数G(ω)和象原函数f(t)之间的相互变换称为傅里叶积分变换，象函数G(ω)和象原函数f(t)构成了一个傅里叶变换对。

积分变换广泛地应用于电学、光学、声学、通信、振动、现代统计学以及化学与化工等多个领域。在聚合物加工流变分析和化工问题中，积分变换是一种非常有用的数学方法。例如，在x射线晶体学中很早就使用了傅里叶变换，液体的结构因子也可以从径向分布函数的傅里叶变换得到，在核磁共振波谱学中，傅里叶变换在缩短实验时间和提高实验灵敏度等方面不可缺少。傅里叶变换和频谱概念有着非常密切的联系。在频谱分析中，傅里叶变换G(ω)称为f(t)的频谱函数，频谱函数的模｜G(ω)｜为f(t)的振幅频谱，显示了频率ω与振幅｜G(ω)｜的关系，简称频谱。由于ω是连续变化，称其为连续频谱。对一个时间函数作傅里叶变换，就是求这个时间函数的频谱。例如振荡型流变仪用于测量小振幅下聚合物材料的动态力学性能，其转子作小振幅的正弦振荡。动态流变和瞬态流变实验用到积分变换。

(2)拉普拉斯(Laplace)变换

在实际工程问题中，许多常用的函数，如单位函数、正弦函数、余弦函数和线性函数等不满足绝对可积的条件；在实际工程问题中，许多以时间t为自变量的函数区间范围为(0，∞)，往往在t<0时是无意义的或者不用考虑，这样问题就不满足函数在整个数轴上有定义的条件，不能应用傅里叶变换。将傅里叶变换的核稍加改造得到了拉普拉斯(Laplace)变换。

拉普拉斯变换是一种重要的积分变换，在自然科学和工程技术中，拉普拉斯变换的理论和方法得到广泛应用。这里仅介绍拉普拉斯的定义和主要性质，便于后面求解本节的问题。

拉普拉斯变换定义 设实变函数或复变函数 f ( t)当 t≥0时有定义，且积分在s的某一域内收敛，则该积分确定的函数可写作

称F(s)为f(t)的拉普拉斯变换，或象函数，记为F(s)＝L[f(t)]。而f(t)称为F(s)的拉普拉斯逆变换，或象原函数，记为

式中，s是复参变量，因为s＝β+iω，所以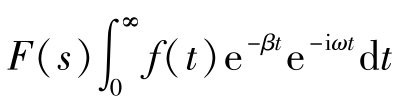，仅当积分收敛(即｜F(s)｜<∞)时，变换才有定义，即

式(6.4.5)是求拉普拉斯逆变换的公式，也称为梅林公式。

从拉普拉斯变换的定义可看出，拉普拉斯变换存在的条件要比傅里叶变换的存在条件弱得多。但是，拉普拉斯逆变化要用到复变函数的积分。不用担心的是，拉普拉斯变换发展成熟完善，用拉普拉斯变换解具体问题时，可使用附录1.4给出的拉普拉斯变换的表格。

简单介绍拉普拉斯变换的性质。若L[f(t)]＝F(s)存在，则有以下性质。

① 线性性质。拉普拉斯变换是线性变换。设L[f₁(t)]＝F₁(s)，L[f₂(t)]＝F₂(s)，α和β是常数，则有

此式表明函数线性组合拉普拉斯变换等于几个函数拉普拉斯变换的线性组合。

② 位移性质。一个象原函数乘以指数函数e^at等于其象函数作位移，则有

③ 延迟性质。若τ为任一实数，且t<0时，f(t)＝0，则有

④ 微分性质。若L[f(t)]＝F(s)，则有

此式表明函数一阶导数的拉普拉斯变换等于该函数的拉普拉斯变换乘以参变量s，再减去函数的初值。

⑤ 积分性质

一般地，有

⑥ 象函数积分性质

一般地，有

⑦ 相似性质。设α为任意正常数，则对于Re(s) >β₀，得

⑧ 与tⁿ乘积的拉氏变换

⑨ 除以t的拉氏变换。若存在，则有

⑩ 初值定理。若极限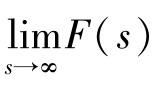存在，则有下列关系

拉普拉斯积分变换一些性质方便了拉氏变换的使用。特别是该拉氏变换的微分性质可把常微分方程的初值问题化为代数方程，把偏微分方程化为常微分方程。正是由于这一原因，拉普拉斯变换成为解微分方程的重要工具。因此它对分析实际的工程的线性系统有着重要的作用。

关于拉普拉斯变换的有关知识，读者可查阅有关数学书^[13]。读者根据自己的基础和时间，学习有关积分变换的知识，可深入系统学习，也可直接接受求解的结果。

有一无限长的平板，其上半空间充满了不可压缩流体，在某一时刻t＝0，平板突然以速度U₀沿x方向运动，如图6.4.1所示。由于黏性的作用，平板上侧流体将随之产生运动，如不考虑重力作用，试分析t>0时刻不可压缩流体的速度场，即求解斯托克斯第一问题^[1,2]。

图6.4.1 平板突然运动

对不可压缩流体流动，此流场具有以下特征：

① 平板x方向无限长，因此在任意一平行于yoz的平面上的流动情况是一样的，即∂/∂x＝0，∂/∂z＝0，u_z＝0，u_y＝0和∂u_y/∂y＝0；(www.xing528.com)

② 平板在z方向无限宽，又平板沿x方向移动，因此流场可以看成是xoy平面上的流场，u＝u_xi，对于平面问题，u_x＝u_x(t，y)；

③ 忽略质量力。根据该流体流动的特点，简化非稳态控制方程式(6.1.1)，得到控制方程

边界条件：①u_x(t，0)＝U₀t>0，②u_x(t，∞)＝0

初始条件：u_x(0，y)＝0，0≤t≤∞。

由于流场突然运动，研究时间变量的范围为0≤t≤∞，可使用拉普拉斯(Laplace)变换式(6.4.4)求解方程式(1)，为了书写的方便，令速度u_x对t的拉普拉斯变换式为

式中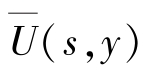，是u_x拉普拉斯变换函数。

用式(3)对方程式(1)作拉普拉斯变换，得到

整理后，方程式(1)变成为

即

由式(3)解出

将边界条件①进行变换，有

即

将式(6)代入式(5)，得

同理，边界条件②的变换为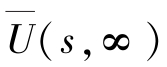＝0代入式(5)，得

将式(7)和式(8)代入式(5)，得

将式(9)进行反变换，得

式中，为误差函数。

式中，用余误差函数表示的速度场，erfcf(z)＝1－erff(z)。

此结果说明在流场的给定点上，流体的速度随时间的增加而增加，只有在t→∞时速度u才能达到U₀；在给定时刻，流体的速度u随着离板面的距离增加而减少，只有在离板面无穷内远处的速度才为零。

斯托克斯第二问题(Stokes 2nd Problem)是作周期振动平板引起的黏性流体的非定常流动^[1,2]。

有一无限长的平板，其上半空间充满了不可压缩流体，在某一时刻t＝0，平板突然以速度U(t)＝U₀cosωt沿平行于x方向做简谐振动，如图6.4.2所示。由于黏性的作用，流场中流体将随之产生振动，如不考虑重力作用，试分析t>0时刻的流场的速度分布。与斯托克斯第一问题相似，控制方程和边界条件为

图6.4.2 平板突然简谐运动

边界条件：①u_x(t，0)＝U₀cosωt，t>0 ②u_x(t，∞)＝0

初始条件：u_x(0，y)＝0，0≤t≤∞。

运用等式e^iωt＝cosωt+isinωt，改写边界条件①为

u_x(t，0)＝Re{U₀e^iωt}

改写问题式(1)的边界条件①为 ③u_x(t，0)＝U₀e^iωt。

假设解为

将式(3)代入式(1)，有

iωU₀f(y)＝νU₀f″(y)

即

运用以上的转换，将偏微分方程式(1)简化为常微分方程

上式的解为

因为i＝e^iπ/2＝cos(π/2)+isin(π/2)，i^1/2＝e^iπ/4＝cos(π/4)+isin(π/4)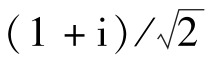＝，式(5)化为

确定式(6)的常数A，B，运用边界条件②，在y→∞＝0时，速度为零，即f(∞)＝0，则A＝0，得

将式(7)代入式(3)式，有

由边界条件③，得B＝1，式(8)化为

取方程式(9)的实部，得到原问题的流速

Tadmor和Gogos在Principles of Polymer Processing^[5]一书列表12.1至表12.4汇总模具各种不同形状口模截面流道流体压力流的流速、剪切应力、剪切速率的流场物理量。有兴趣的读者和科技人员可以使用这些表，有针对性地解决工程问题。本书附录1.2给出这几个表。需要注意的是，按照Tadmor应力的正负号约定，表示应力公式多一个负号，需要使用他的应力表示的运动方程求解问题。