圆柱管流道中非等温压力流体的优化策略

管道中的压力流存在于许多聚合物流变测量仪器和聚合物材料加工过程中，比如毛细管流变仪、熔融指数仪、挤出机口模、注射模具流道中。按管道截面形状不同，又分为圆形管道，矩形管道，异形流道等多种。物料在管中流动，是因为管道两端存在压力差，因此称压力流(Poiseuille flow)。现在，以圆形管道为例，讨论流体在压力作用下，在管中流体的非等温流动情况^[11,12]。

设管道内径为R，长度为L，在管道内取柱坐标系(r，θ，z)如图6.3.2所示。物料沿z方向流动，在不同半径r处物料流速不等，故r方向为速度梯度方向；θ方向为中性方向。

图6.3.2 圆形管流道的非等温压力流(Non-isothermal Poiseuille flow)

同样，根据流体流动的特点，对流动情况作适当的简化假定：

① 流体为不可压缩非牛顿型黏性流体，流动为稳定的层流，设管径R≪管长L，此流动为轴对称流动，u_r＝0和u_θ＝0，速度为u＝u_z(r)e_z，且u_z(r)只有沿r方向的速度梯度分量∂u_z(r)/∂r≠0。

② 稳态流动∂/∂t＝0，且流体为水平层流，忽略质量力g_z＝0；

③ 在管壁物料无滑移，偏应力张量中有τ_zr＝τ_zr≠0；

④ 设流体内压力p沿z方向有常数的梯度∂p/∂z，忽略质量力和惯性力；

⑤ 温度场不随时间变化∂T/∂t＝0，管壁温度保持恒温T_w，圆管流道内没有热耗损和对流传热，即温度场T＝T(r)；

⑥ 采用幂律方程来描述黏性流体的流动。

由假设条件①，将柱坐标系连续性方程式(3.2.11b)，简化为

由式(1)和假设条件②~④，简化柱坐标系的N-S方程式(3.2.28b)，有

r方向

θ方向

z方向(www.xing528.com)

由假设条件⑤，简化能量方程式(3.2.53b)，得到

速度边界条件： ① 自然边界条件，② 壁面无滑移条件u_z(r＝R)＝0。

温度边界条件： ①T(R)＝T_w，② 自然边界条件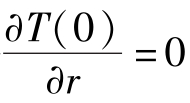

根据假设条件⑥用幂律流体的本构方程描述该流体的流动

略推导过程，读者在练习题中用分离变量法，解上述方程定解问题，得到幂律流体流过圆管的压力流场中的速度场^[11]和温度场^[12]

式中，κ为流体的导热系数，K为幂律流体的稠度，n为幂律指数(非牛顿指数)。

讨论分析式(6.3.3)和式(6.3.4)可知，管壁处无滑移(r＝R)，得到物料的流速为零，管壁的温度为T_w。管道轴心处(r＝0)速度最大，物料总是沿着压力下降方向流动。管道轴心处的流速和温度分别为

由这两个计算式可看出，流速和物料温度均在管道轴心处取极大值，轴心处物料温要比管壁温度高许多。

若令式(6.3.4)和式(6.3.5)中，牛顿指数n＝1，得到黏度μ的牛顿型流体流经圆形管道的速度分布和温度分布

由以上两个公式可知，管道内牛顿型流体速度分布按二次抛物线的规律变化的，而温度分布则按四次抛物线的规律变化。可见，从管壁到轴心线，物料温度增长的速率比速度的变化快得多。

将速度式(6.3.3)代入计算圆管的流量式q_V＝∫2πru_zdr，计算流量和平均速度，得到

科研工作中，为了研究流体流动的普遍规律，常常将流场的物理量无量纲化。这是定性分析流体流场的一个好方法，可用于讨论流体流动普遍规律。本书没有详细介绍这方面的内容。这里给出一例。用管中的平均速度定义量纲为1的速度和温度函数，分别为

图6.3.3给出圆管流道幂律流体无量纲速度随r/R和n的变化。由此图可见，n<1的假塑性流体的流动前呈无柱塞状，n>1的胀流性流体的流动前呈前突状。

图6.3.3 圆管流道幂律流体无量纲速度随r/R和n的变化^[12]