圆管流道压力流分析

在管材挤出口模内，聚合物流体的流动属于圆管流道的流动。19世纪G.H.L.哈根和J.L.M.泊肃叶从实验归纳出圆管液体层性管流的流动规律，后来证实与精确解符合。圆管流道流体的压力流称为泊肃叶流(Poiseuille Flow)。本小节分析圆管流道和锥形管流道的聚合物流体压力流，包括圆管流道流体的压力流、两圆柱同轴环隙流道流体轴向压力流、锥形圆流道流体的压力流3部分。

当雷诺数小于2000时，等截面直圆管中的液体流动是层性管流。在压力驱动下，长圆管流道不可压缩黏性流体做等温稳态层流，是平行单向流的另一种情况。假设圆管长L和管内半径R，其中L≫R，如图6.1.8所示。流体在远离圆管流道进口处作稳态流动，用柱坐标方程求解该问题。根据流体流动特征，分别简化柱坐标系不可压缩流体的连续性方程和运动方程，用两种方法分析该流动。

图6.1.8 长圆管流道稳态平行层流

(1)求牛顿流体流场的精确解^[1，2]

此流动为轴对称流动，u_r＝0和u_θ＝0，速度分布为u＝u_re_r+u_θe_θ+u_ze_z＝u_z(r)e_z。

将柱坐标系连续性方程(3.2.11b)

简化为

由于是稳态流动，∂/∂t＝0，∂u_z/∂t＝0；且流体为水平层流，忽略质量力g_z＝0，简化柱坐标系的N-S方程(3.2.28a)，有

r方向

θ方向

z方向

边界条件： ① 自然边界条件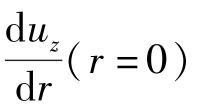＝0；② 壁面无滑移条件u_z(r＝R)＝0

在r方向和θ方向有和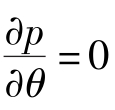，即p＝p(z)，式(4)中偏微分可换成常微分，分离变量后，得

将式(5)改写为

积分式(6)中等式右边项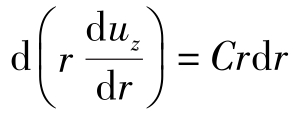，有

运用边界条件①和②，得C₁＝0，代入式(7)，有

进一步积分式(8)，得

将式(6)代入式(9)，得

式中，R为圆管内半径。

对速度体积分，得到长圆管流道的体积流量

这就是著名的泊肃叶压力流动的解，即N-S方程的典型精确解。

当r＝0，得圆管流道最大流速为

比较式(6.1.25)与式(6.1.27)，有u_z(r)＝u_zmax[1－(r/R)²]

u_{z max}＝2u_b

z方向上的总压力梯度为

当流体的动力黏度μ、来流主体流速u_b和圆管内半径r_i已知时，就可计算此流动的压力降和流速分布。

(2)若假设该流动为幂律流动，确定流场的物理量^[3]

根据流体流动的特点，简化不可压缩流体柱坐标系连续性方程(3.2.11b)和N-S方程(3.2.28b)，有

r方向

θ方向

z方向

将式(4)分量变量，有

由式(1)可知u_z＝u(r)；由式(2)和式(3)可知p＝p(z)，式(5)的左边不依赖r，等式右边不依赖于z，只能是等式的两边等于常数C。使用两平板间流体的稳态流动推导的方法，可得到剪切应力为

对于非牛顿流体，若假设该流动为幂律流动，此处略去推导过程。在练习题中，读者完成详细的推导过程，确定长圆管流道流场的物理量^[3]，为

流体流速

体积流量

平均速度

剪切速率

壁面剪切速率

对于牛顿流体，n＝1和K＝μ，得到体积流量和流速分布与牛顿流体流场的精确解的结果相同，分别为

(3)体积流量方程的分析

已得到体积流量式(6.1.30)，为(www.xing528.com)

由上式可知压力降与体积流量成正比

假设圆管长L和管内半径R不变，由Δp∝q_V，为了讨论牛顿指数n的影响，假设

式中，k>1。

用上式定性地分析不同的聚合物流体：

① 牛顿流体，牛顿指数n＝1，＝k

② 假塑性流体，牛顿指数n<1，

③ 膨胀性流体，牛顿指数n>1，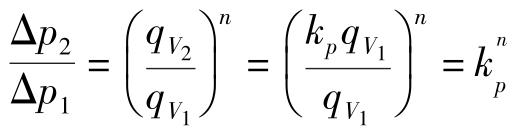

由以上分析可看出，，假塑性流体的压力梯度最小。当圆管尺寸和流体的体积流量基本不变的情况下，增加聚合物流体的假塑性，有利于节电节能。这个定性分析得到的结论对聚合物加工成型有指导作用。

(4)流速与平均流速比值的分析^[4，9]

已经得到流场的速度式(6.1.29)和平均速度式(6.1.31)，分别为

流体流速

平均速度

由上两式，得到速度与平均速度的比值

讨论式(6.1.36)可知，对于幂律流体，管中心轴线上流速最大，有

当n→0的极限情况

n值分别取为0，0.1，1,2和∞，作图6.1.9。此图给出长圆管流道压力流u_z(r)/u_b随r/R的变化。分析式(6.1.36)，当n＝1，牛顿流体速度与平均速度的比值为抛物线方程，如图6.1.9(c)所示。

当指数n→∞，速度与平均速度的比值为一直线方程，如图6.1.9 (e)所示。

对于膨胀性流体n>1，速度分布曲线变得尖锐， n值越大曲线越接近锥形；对于假塑性流体n<1，速度分布曲线较抛物线平坦， n值越小管中心部分的速度分布越平坦。当n→0时速度分布曲线形状类似于柱塞，故称这种流动为柱塞流 (plug flow)或平推流。

图6.1.9 不同n值长圆管流道压力流u_z(r)/u_b随r/R的变化^[9]

(a)n＝0(b)n＝0.1(c)n＝1(d)n＝2(e)n＝∞

(5)柱塞流动的分析^[5，9]

如图6.1.10所示，柱塞流动可以看成是两部分流动组成。在r>r^∗区域内为剪切流动，在这一区域剪切应力大于屈服应力，即τ>τ_y。在r^∗区域内为柱塞流，在这一区域剪切应力小于屈服应力，即τ<τ_y。

图6.1.10 长圆管流道柱塞流的速度分布^[4]

图6.1.11比较长圆管流道柱塞流与抛物线流的差别。由此图可知，在柱塞区的流体表现出类固态(Solid-like)的流动行为，流体像塞子一样沿受力方向移动。由于流体受到剪切应力很小，聚合物流体不能很好的混合，均匀性差，降低制品的性能。柱塞流动不利于聚合物加工成型。抛物线形流动是流体受到较大的剪切应力，在流经挤出口模或注塑的喷嘴时产生的涡流，增大了扰动，提高了材料的混合均匀程度，有利于聚合物加工成型。

图6.1.11 圆管流道柱塞流与抛物线流的比较

(a)柱塞流(b)抛物线流

管材挤出口模由同心圆管外半径R_o和内半径R_i环隙的组成，管长L，其中L≫R₀/R_i。在压差Δp的驱动下，两圆柱同轴环隙流道流体做稳定等温的层流^[3]。当L≫R₀/R_i时，挤出的体积流量，可使用平板间的压力流动式近似计算。当R₀/R_i＝H比值越小，计算误差越小，可按稳定等温层流的轴向压力流分析，获得精确解。

此流动为轴对称流动，u_r＝0和u_θ＝0，速度分布为u＝u_re_r+u_θe_θ+u_ze_z＝u_z(r)e_z稳定流动有∂/∂t＝0和∂u_z/∂t＝0，且流体为水平层流，忽略质量力g_z＝0。运动方程和圆管流道的情况一样，在u_z(r＝R₀)＝0和u_z(r＝R_i)＝0的边界条件下，得到两圆柱同轴环隙流道内速度分布

式中，κ＝R_i/R₀<1。

对速度积分，得体积流量

对于幂律流体，可以得到速度的分布，最大速度靠近内圆管的一侧，且偏离环隙中心。

分析锥形管流道流体的压力流^[4]。管材挤出口模是锥形圆管，如图6.1.12所示，锥管大头半径R₀，小头半径R_L，管长L，其中L≫R₀，R_i。在压差Δp的驱动下，锥形管流道流体做稳定等温层流。分析锥管流道内流体的流动特点，可知压力仅是z的函数p＝p(z)，但是速度不同于直圆管，流体的速度是r和z的函数，即u_z＝u_z(r，z)。

图6.1.12 锥形流道的几何形状

锥管半径R随z渐变，锥角小于30 ^o，锥管半径R可表示为

压力降为

将式(1)和式(2)代入直圆管内流体的平均流速(6.1.31)

得到求解压力p＝p(z)的一阶微分方程，为

压力边界条件： ①p(z＝0)＝p₀②p(z＝L)＝p_L

积分式(3)，应用边界条件①和②，得到

近似方程式(6.1.39)对于锥管的锥角小于30^o是可用的。对于环锥形流道和异形截面流道流体的流动感兴趣的读者，可参看有关文献[5,7]。