平板流道中流体压力流的模拟与优化

在板材、片材挤出口模内，聚合物流体的流动属于平行平板流道的流动。本小节分析平行平板流道和矩形流道流体的压力流，包括平行平板流道流体的单向流动、平行平板流道流体的二维压力流、矩形流道内流体的压力流、等截面矩形狭缝流道流体的压力流、平板壁面质量力驱动的流动5部分。

流体最简单的一类流动是平行平板流道不可压缩流体的平行流动，称该流动为单向流动(Unidirectional Flow) ^[1,2]。假设两块平行平板长L、板间宽b和板间间隙H，其中L≫b，至少L/b≥10，b≫H，称其为无限大的平行平板。在压力驱动下，在无限大的平行平板流道，流体做充分发展的等温层流。

为了分析平行平板流道黏性流体的单向流动，根据流体的性质和流动的特点，做出合理的假设条件：

① 流体是不可压缩的流体，有Δ·u＝0；

② 单向流动，流体的流场仅有一个方向的速度，有u_y＝u_z＝0；

③ 所考察的部位是远离流道进出口的地方，流动是充分发展非稳定流动，流场所有的物理量随时间变化，有∂/∂t≠0；

④ 等温层流，没有热量传递，可忽略黏性热耗散，不用考虑控制方程的能量方程，且状态方程的ρ＝常数，μ＝常数；

⑤ 驱动力仅有压力，忽略质量力；

⑥ 壁面边界无滑移，有边界条件u_x|_{y＝± H/2}＝0和自然边界条件∂u_x/∂x|_y＝0＝0。

在以上假设条件下，简化不可压缩黏性流体流动的控制方程式(3.3.2)。由假设①和②，流体的流场仅有一个方向的速度u＝u_xi，因此在x方向方程连续性简化为

微分式(1)可得

由假设条件③、④和⑤，简化运动方程为

将式(1)和式(2)代入式(3)，考虑单向流动u＝u_xi，同样的方法简化y，z方向的运动方程，最终运动方程化简为

由运动方程式(5)和式(6)了解到驱动力仅为x、t函数

分析仅有的运动方程式(4)，可见速度和压力只能是时间的函数，将其分离变量，令等式两边等于常数C(t)，得到单向流动的控制方程为

分离变量后，有

式中，μ为黏度，对牛顿流体是常数；C(t)为随时间变化的常数。

当稳态流动中，它是常数C，控制方程简化为

下面用运动方程的简化式(6.1.1)，分析求解一些平板间黏性流体的流动。首先分析两平行平板流道流体的稳态流动^[1-3]，该问题的解是N-S方程典型的精确解。

在两层具有无限长和宽度的平行平壁之间，在压力驱动下，不可压缩黏性流体作充分发展稳定层流(laminar flow)。假设两块长L、板间宽b和板间间隙H，其中L≫b，至少L/b≥10，b≫H。流场所有的物理量不随时间变化，有∂/∂t＝0，壁面无滑移。画出平行平板流道稳态平行层流的示意图6.1.1。所考察部位是远离流道进出口的地方。由该定常流动的特点可知，流速为u＝u_x(y)i，其中∂u_x/∂t＝0和∂²u_x/∂z²＝0，化简偏微分方程式(6.1.1b)为常微分方程为

图6.1.1 平行平板流道稳态平行层流

将式(1)分离变量后，有

压力边界条件：①p(0)＝p₀，②p(L)＝p_L，

速度边界条件：③u_x(－H/2)＝0，④u_x(H/2)＝0

积分式(1)，得

运用压力边界条件①和②，确定式(4)中的积分常数为

由式(5)确定常数C，有

积分式(3)得

对式(7)分别运用速度边界条件③和④，得

由式(8)和式(9)确定积分常数为

将积分常数式(6)和式(10)代入式(7)，得到速度与压力梯度关系为

在y＝0处，流速最大为，则

式中，Δp＝p₀－p_L。

确定流量，在x方向上，通过两平行平板流道单位宽度(z方向）的体积流量为q_V/b＝q_Vu，q_Vu是速度的单位宽度体积积分，为

u_b为主体流速(Bulk Velocity)，由q_Vu＝u_bH，用压力表示的主体流速u_b为

则压力降为

当流体的动力黏度μ、来流主体流速u_b和流道宽H已知时，就可计算此流动的压力降和流速分布。

确定流场的剪切应力式(2.3.13)

确定壁面的剪切应力

前面牛顿流体流场的解是N-S方程典型的精确解。下面分析非牛顿流体的流动。由于复杂的非牛顿流体的流动控制方程不能解析求解，定性地分析简单截面流道聚合物流体的流动问题，常常采用幂律本构方程描述流体的流变性能。

用幂律本构方程(5.2.18)得到描述非牛顿流体的剪切速率与剪切应力的关系，有

将式(11)代入式(12)，分别得到流场任意一点剪切速率和板壁的剪切速率

积分流场的变形速率式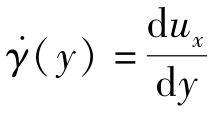，得到速度积分式

将式(6.1.8)式代入积分式(13)，计算非牛顿流体的速度^[3]

最后得到非牛顿流体用幂律指数表示的流场速度分布式

对上式求速度的导数，得

用速度式(6.1.10)计算幂律流体x方向单位宽度体积流量，得到

分析两平行板流道幂律流体层流的速度分布式(6.1.8)的极限情况：

① 当y＝H/2，u_x＝0.，速度式满足壁面无滑移的条件；(www.xing528.com)

② 当y＝0，流速最大，。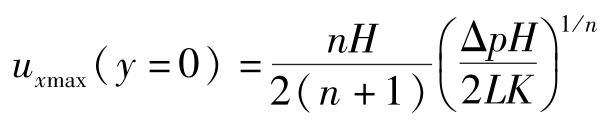

矩形流道长L宽b高H如图6.1.2所示，宽高比b/H<(10~20)。在压力驱动下，矩形流道内流体沿着z轴做稳定等温层流，所考察部位是远离流道进出口的地方，不用考虑边界的影响，所有的4个侧壁上u_z＝0，其他假设同前面的分析。由于矩形流道的宽度和高度是同一数量级，矩形流道内流体的压力流不再是单项平行流动^[3]。

图6.1.2 矩形流道

首先定性地分析矩形流道内流体的压力流。在层流状态下，矩形流道截面的聚合物熔体速度以环形等速线分布，在所有的方向上剪切速率分布不均匀。矩形流道截面中心的剪切速率为零。矩形流道长边中心线方向的剪切速率升高的最快也最大，而短边方向就较小。因此，随着剪切速率增加挤出膨胀更显著。实验的测定已经证实，矩形口模长边中心处的压力和挤出物膨胀比比短边中心大，矩形口模任一给定的出口压力和挤出物膨胀比随着体积流量的增加而增大。

这里略去了复杂的求解过程，仅介绍确定矩形流道流体的体积流量。下面分别分析矩形流道牛顿流体和非牛顿流体的流动。

(1)牛顿流体

分析压力驱动的矩形流道牛顿流体稳定等温层流的特点可知，流场所有的物理量不随时间变化∂/∂t＝0，流速为u＝u_z(y)i，其中∂²u_z/∂z²＝0和－∂p/∂y＝0。简化控制方程(3.3.2)，得到描述该流动的控制方程。N-S方程z向分量简化为

由壁面无滑移，得到速度边界条件

① u_z(x＝±b/2)＝0，②u_z(y＝±H/2)＝0

由于－∂p/∂y＝0，分析式(1)可知，z向的压力梯度为常数，与平行板间流动类似，有

将式(2)代入式(1)，有

用分离变量的方法求解运动方程式(3)，略推导过程，用傅里叶级数表示解。使用边界条件，得到总体积流量为

式中，F_p为形状因子。它是矩形截面高宽比的函数F_p＝f(H/b)。

当形状因子F_p→1，与平板间流体单位宽度的体积流量计算式(6.1.4)相同

图6.1.3给出了形状因子F _p随H/b的变化。对于牛顿流体，当H/b＝1/10时，考虑侧壁对流动的影响F _p＝0.95，比平壁减少了5%。当H/b＝1/20时，两侧壁对体积流量的影响更小。

(2)非牛顿流体^[3，4]

当流体是非牛顿流体时，N-S方程是非线性偏微分方程，不能解析求解。只能用数值积分求解。若非牛顿流体用幂律方程表示，得到总体积流量为

式中，S_p为形状因子，S_p＝f(b/H，n)，即它是矩形流道截面宽高比b/H和流动指数n的函数。

图6.1.4给出了矩形流道幂律流体形状因子S_p随b/H和n的变化。形状因子与流动指数n的关系为

将式(6.1.15)代入式(6.1.14)，得到矩形流道流体的总体积流量

式中，S_q为矩形流道两侧壁对流量影响的修正系数。

图6.1.3 矩形流道牛顿流体F_p随H/b的变化^[3]

图6.1.4 矩形流道幂律流体S_p随b/H和n的变化^[3]

若n＝0.5，则^＝0.125。取图6.1.4上的若干点，汇集到表中。表6.1.1给出不同宽高比b/H的形状因子S_p和修正系数S_q。

表6.1.1不同宽高比的形状因子S_p和修正系数S_q(n＝0.5)^[4]

一般工程上，计算工程误差为5%。由表6.1.1可知，对于牛顿流体，矩形流道与平行板间隙以H/b＝1/10为界限；对于非牛顿流体，以H/b＝1/20为界限，可以用平行平板流道的压力流方法分析流体的流动。

在挤出板件的挤塑过程中，狭缝流道是常见的刚性边界。用6.1.1.2平行平板流道黏性流体二维压力流，分析等截面矩形狭缝流道流体的压力流^[4]。高聚物黏度高，热传导性能差，它的制品只能是薄壁板件或薄板的组合，因此成型模具是狭缝矩形型腔。垂直流动方向的宽度b与缝隙高度H的比，b/H>(10~20)，如图6.1.5所示。这里略去详细的推导过程，用比较法求解问题。忽略狭缝流道两侧壁对流量的影响，将两平行板流道非牛顿流体的速度分布式(6.1.10)演化为狭缝流道压力流动的流体速度，为

图6.1.5 等截面矩形狭缝流道b/H>(10~20)

对速度式(6.1.17)体积分，忽略两侧壁对流量的影响，计算通过狭缝流道熔体的总体积流量

将速度导数式(6.1.11)的速度导数代入剪切应力的公式，对于非牛顿流体，黏度μ等于稠度K，得到流场中任一点的剪切应力

由式(5.2.18)，可得到描述剪切速率与剪切应力的关系式

将式(6.1.19)代入上式，得到流场的剪切速率

将式(6.1.18)两边n次方，整理化简得

将式(1)与式(6.1.20)对照，可分别得到狭缝矩形流道幂律流体流动壁面剪切速率和剪切应力

对于牛顿流体n＝1，得到牛顿流体在狭缝通道壁面的剪切速率为

当两块平板间距组成可变间隙H(x，z)的流动区域，下部平板以速度U₀运动并移动，上部平板缓慢地起伏，在两平板变间隙的流道流体流动，该流动问题就变成了二维问题。Tadmor^[5]给出假设条件简化N-S方程，详细求解了上板运动，下板固定的非平行两板间流道流体流动。图6.1.6给出两相对运动非平行两板流道流体流动的速度分布。

图6.1.6 两相对运动非平行两板流道流体流动的速度分布^[5]

由此图可见，当入口压力和出口压力相等时，在入口区域速度有回流，随着压力升高速度增大到达某一区域，流道内速度是线性分布，随后流体达到压降区域，速度分布从壁面的零到最大值，呈现前凸曲线。

关于变截面、楔形、鱼尾、两偏心圆环等其他形状流道聚合物流体的流动，有兴趣读者可参看有关文献[2,5,7]。

仅有质量力驱动的不可压缩流体流动也是平行单向流的一种^[1]。无限宽平板与水平地面的夹角为α，如图6.1.7所示。流体由质量力在平板上作定常层流，确定该流场的速度分布。由于平板无限宽，两侧边界的影响可忽略，问题可化简为平面流动；由于平板足够长，两端的影响可以不考虑；流体仅沿u＝u_x(y)i轴方向流动，考虑质量力。简化非等温不可压缩均质流体流动的控制方程式(3.3.2)为

图6.1.7 平板上的质量力驱动平行流

压力边界条件： ①p(y＝H)＝p_atm。

速度边界条件： ②u_x(y＝0)＝0，③ 在边界上，∂u_x/∂y(y＝H)＝0

积分式(2)，得

由压力边界条件①，得

将式(4)代入式(3)，得

请运用式(5)和速度边界条件②和③，在作业中，读者完成此问题的详细推导过程，确定该流动的体积流量为