选择合适的本构方程描述自己研究的问题，对于聚合物加工过程，首先判断聚合物流体流动的特性[6]，根据流体的特性选择本构方程。
针对如何选择本构方程？本小节介绍本构方程选择的方法和原则，包括判别聚合物流体流动的特性、选择本构方程的基本原则两部分。
用已有的实验数据和黏弹性相关的参数判断流动过程黏性效应和弹性效应的相对重要性。什么时候可使用纯黏性的模型？
(1)用法向应力差函数判别流体的特性
第3.1节介绍了第一和第二法向应力差函数，分别为式(3.1.44)和式(3.1.45)
N 1＝τ11－τ22，N2＝τ22－τ33
若聚合物流体的法向应力差函数 N 1＝N2≈0，则可认为流体属于纯黏性流体。
(2)用可恢复剪切应变 SR判别流体的特性
可恢复剪切应变是材料的弹性应力和剪切应力之比式(4.1.9)，为
式中，SR是无因次应力。
对于稳定剪切流动，如果流体有足够的流变数据，可以先判断可恢复剪切应变。SR越小，表明流体的弹性作用越不明显；SR越大，弹性作用越强。如果SR≪1，弹性应力比黏性应力相对来说就不重要。因此，可以用纯黏性本构方程描述该流体的流动过程。
(3)计算流体的松弛时间 λ判别流体的特性
第5.2节得到，判别不可压缩黏弹性流体流变特性的流变状态方程式(5.2.14)和式(5.2.16)，分别为
将上两式代入可恢复剪切应变式(4.1.9)，可得到
式中，λ为Maxwell麦克斯韦流体松弛时间。
计算流体的松弛时间tλ和过程的特征剪切速率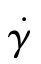
的乘积
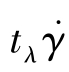，判断黏性效应和弹性效应的重要性。如果
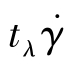很小，可以断定弹性效应很小。
由于法向应力数据往往不易找到，特别不容易得到高剪切速率下的数据；反之松弛时间一般可从材料线性黏弹性估算出来，动态力学的研究比法向应力研究更为普遍。因此，用松弛时间tλ比用可恢复剪切应变SR判别流体的特性方便一些。
这里介绍选择本构方程的应遵循的基本原则，并用两个实例说明。
(1)黏弹模型必须能表征实际黏弹流体基本特征
所选的黏弹模型需要从以下两个方面满足对实际黏弹性流体的基本特征。
① 剪切流动中出现法向应力；
② 能够解释表征瞬时现象的应力生长函数η+，还能解释包括经典应力松弛现象在内的各种瞬时现象。
定义应力生长函数η+为
可见，应力生长函数η+是时间的函数，当时间t→∞，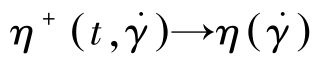
。
(2)根据加工成型方法的特点，确定选择本构方程
例如，在中空吹塑时，需要用黏弹模型估算离模膨胀；在纤维纺丝时，所选的黏弹模型主要反映拉伸黏度的特性，而不是法向应力差。在低速下，加工成型高黏度聚合物熔体，可近似将其作为牛顿流体。如果在较宽的剪切速率范围内加工成型，随剪切速率的提高，材料流变行为由牛顿型过渡到非牛顿型，则可用Carreau等模型。
(3)预示的材料流变性能与实际基本复合
由于牛顿型流体模型、幂律模型等本构方程形式简单、参数较少，聚合物发展的早期使用广泛，特别用于分析简单截面流道的流体流动。尽管这些多参数的Carreau、Cross、HB本构模型的物理意义不够明确，现在常被用于聚合物加工流场的分析、流变测量数据的处理、模具和设备设计的软件中。在挤出、注塑、纤维纺丝、薄膜吹塑、热成型等聚合物加工过程中，材料的加工的流变行为不仅与黏性有关，还与弹性有关，则需要用本章介绍的描述材料黏弹性的本构方程。(www.xing528.com)
下面用两个实例，说明已经介绍的几个模型的使用情况。
实例5.3.1[9]1987年，美国Virginia Polytechnic Institute and State University的教授D.G.Baird的博士生A.D.Gotsis的博士论文“Numerical Simulation of Viscoelastic Flow(黏弹性流体的数值模拟研究)”，使用上随体Maxwell(UCM)模型、White-Metzner(W-M)和Phan Thien-Tanner(PTT)3个本构方程，数值计算预测了聚苯乙烯流变曲线，将数值模拟的计算结果与190 °C聚苯乙烯(Styton 678道化学公司)实验测得的流变数据比较，图5.3.1、图5.3.2和图5.3.3分别给出研究结果。
图5.3.1 UCM，W-M和PTT模型对聚苯乙烯黏度的预测值与实验数据的比较[10]
分析图5.3.1、图5.3.2和图5.3.3，可得到几个结论：
① W-M模型和PTT模型能显示出聚苯乙烯的剪切变稀行为，而UCM模型预示了牛顿流体的行为，与实际情况偏离；
图5.3.2 UCM，W-M和PTT模型预测第一法向应力差的值与实验数据的比较[10]
图5.3.3 UCM，W-M和PTT模型对拉伸黏度ηe预测值与实验数据的比较[10]
② W-M模型预示的第一法向应力差与实验更接近；
③ 在预示拉伸黏度ηe方面。因为在低剪切速率下，拉伸黏度是零剪切黏度的3倍，即ηe＝3η0；随着拉伸速率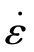
的增大，ηe也增大。但是，UCM模型和W-M模型是无约束的增大，而PTT模型先增加，到最大值后又下降。
这个实例说明，W-M模型和PTT模型能较好地预测聚合物的流动特性，虽然在极限情况下，都有一定的误差，PTT模型更好一些。对于聚合物流体最好使用更复杂多参数本构模型。在聚合物加工成型中大量应用的事实说明了这点。
实例5.3.2 2003年，根据某公司要求，朱敏和陈晋南等[11]测试了橡胶ACDF的流变数据，使用软件确定了Carreau模型参数η0＝5.5×106Pa·s， λ＝130和n＝0.2，根据所需产品截面的具体尺寸，初步绘出口模的模型图，逆向挤出数字设计了桑车橡胶密封C条异型材直流道和非直流道结构的口模，图5.3.4 (a)给出直流道口模的几何尺寸。如图5.3.4 (a)所示。假设AB为流体所选求解域进口，给定进口体积流量qv＝7.5×10－6m3/s； DE为流体所选求解域出口，假设此处牵引力为零， CDEF为挤出物自由表面，口模壁面ABCF为流体所接触的内壁，假设口模壁面速度为零的条件下，在计算机上进行了挤出实验和修模，根据流场分析进行逐步修模，经过56次的修模和计算，最终确定了口模的流道结构和尺寸。另外，非直流道模型平面为对称面。
数值模拟了口模直流道和非直流道挤出橡胶的等温过程，计算速度场、压力场和剪切速率场。图5.3.4 (b)给出模具内和出口处物料压力分布，图5.3.4 (c)给出产品与数字设计模具产品的截面。
图5.3.4 汽车橡胶密封C条挤出模具的数值研究
(a)直流道几何模型，mm(b)非直流道模具内和出口处物料压力分布(c)产品与数字设计模具产品的截面
研究结果表明，从口模入口到出口压力逐渐下降，口模外部熔体的压力最低而且分布很均匀。这是因为口模壁面的剪切作用，压力降主要发生在口模内部。物料挤出口模后，由于不受外力而处于大气压下的自然状态，因而压力降较小且趋于零。最大的剪切速率出现在口模壁面沟槽位置处。数字设计口模挤出物截面与产品截面形状和尺寸大体一致，吻合较好。变化较为剧烈的边角沟槽处与实际还有一定的差距，计算相对误差为9.87 %。非直流道的相对误差6.94%小于直流道的相对误差11.47%。
2008年，陈晋南和吴荣方[11]再次深入研究了桑车橡胶密封C条异型材的口模。用Pow-er模型和近似Arrhenius式的乘积描述橡胶表观黏度的非等温本构方程，12次逆向挤出数字设计了口模直流道结构尺寸。在进口体积流量为qv＝7.5×10－6m3/s，进口温度和壁面温度为373K，自由表面温度为303K的条件下，数值模拟桑车密封件C条橡胶口模的等温和非等温挤出过程，坐标原点选在口模进口截面的右下角，流体流动方向为z轴，其中口模ABEF长14.2mm，挤出橡胶熔体BCDF长27.8mm。用4面体网格划分熔体ACDF。在口模出口和壁面附近熔体流场变化剧烈处网格适当加密，网格总数为11424个。图5.3.5分别给出了桑车密封件C条的截面、直流道截面的尺寸和几何模型的网格划分。在HPXW6000工作站上完成计算，计算收敛精度为10－3，最长一次运算机时是3.5h。图5.3.6至图5.3.8给出数值计算结果。
图5.3.5 几何模型和网格划分
(a)密封件C条的截面(b)设计的直流道截面(c)几何模型网格划分
图5.3.6 口模内熔体部分的流场
(a)速度场，m/s (b)压力场，MPa (c)剪切应力场，MPa (d)黏度场，kPa·s
分析讨论了温度对口模结构尺寸和橡胶熔体流变行为的影响，如图5.3.7所示。由图5.3.7可知，沿熔体流动的方向，非等温熔体的平均速度和平均压力比等温的大，平均剪切应力和平均黏度都低于等温。图5.3.8给出了非等温和等温模拟计算的结果与实际样品截面的比较。由图5.3.8可知，非等温直流道的模拟结果除了在尖角地方(x方向10~15mm处）的差异较大，模拟的结果与产品的形状基本一致。从相对误差来看，非等温的平均相对误差仅为1.63%，远小于等温的12.31%。非等温截面尺寸最大误差为5.04%，其在工程误差允许范围内。
图5.3.7 口模内沿Z轴流道不同截面熔体的物理量平均值的变化
——■——等温 ——▽——非等温
(a)平均速度 (b)平均剪切应力 (c)平均压力 (d)平均黏度(e)平均温度
文中还比较了使用Carreau模型数值模拟研究的结果[12]。该科研实例比较说明了使用Power模型和近似Arrhenius式的乘积描述橡胶表观黏度的非等温本构方程与Carreau模型的具体情况。尽管数值计算中，简化边界条件简单。研究结果可以表明，非等温的数值模拟更接近口模挤出的实际情况。采用非等温的本构方程设计口模将提高口模和产品的质量。
图5.3.8 非等温和等温模拟计算的结果与实际样品截面的比较
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
