广义牛顿流体的本构方程探析

经过几十年的发展，建立很多广义牛顿流体的本构方程。本小节介绍广义牛顿流体的本构方程，包括不可压缩牛顿流体应力张量和变形速率张量的不变量、几种广义牛顿流体的本构模型两部分。为了读者使用方便，本节给出本构方程张量和注记符号的表达式，具体本构模型仅给出数量形式表达式。

假设流体是各向同性的，应力张量和应变速率张量是线性齐次函数关系，得到不可压缩牛顿流体张量形式的流变方程为

或写成注记符号分量式

为了描述描述非牛顿流体的黏性特性，用非牛顿黏度或剪切黏度η代替牛顿流体的黏度μ，得到广义牛顿流体的本构方程

因为黏度是标量，它必须是变形速率张量或剪切应力张量3个不变量（标量）的函数。为了后面章节使用公式的方便，将第3.1.2.2节应力张量3个不变量中所有的应力用τ_ij表示，定义应力张量的3个不变量式为

其中，应力张量(Magnitude of the stress tensor)的大小为

3个应力张量的不变量具有重要的几何和物理意义。由广义牛顿流体的本构方程可知黏度是应力张量的函数，由此可知黏度也是这3个应力不变量的函数，有

由于工程中，常用标量应变速率张量或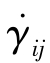表示剪切应力与变形的关系，为了讨论问题的方便，后文中变形速率用符号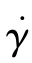，变形速率张量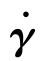表示为

在外文聚合物加工的专著^[6]中也用Δ或Δ_ij表示的应变速率张量，有

在第3章曾介绍直角坐标系、柱坐标系和球坐标系的变形速率张量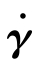分量，其中直角坐标系应变速率张量的分量式(3.1.46)、柱坐标系应变速率张量的分量式(3.1.47)、球坐标系应变速率张量的分量式(3.1.48)。

鉴于应变速率张量的重要性，这里从几个方面说明变形速率张量的主要性质和物理意义。

(1)二阶应变速率张量 是对称张量

从式(5.2.6)可知，二阶应变速率张量仅有6个独立的分量，包括3个对角线分量和3个非对角线分量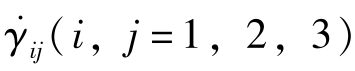。因此，二阶应变速率张量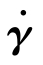也是对称二阶张量。

(2)应变速率张量的不变量

对称的应变速率张量有3个不变量。下面定义这3个不变量。

第一不变量

第二不变量

第三不变量

式中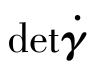，是由的分量组成的矩阵行列式。

假定黏度η依赖于的分量定义的流动运动量。由广义牛顿流体的本构方程可知黏度是一个标量函数。但是，不一定是常数。因此，黏度必须是应变速率张量3个不变量（标量）的函数，有

对于不可压缩流体，有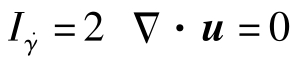。对剪切流动，；对于近似剪切流动，也可以忽略去黏度η对第三不变量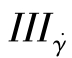的依赖。非牛顿流体的黏度只是第二不变量的函数，有。由于二阶张量的对称性，将代入第二个不变量，且对于简单剪切流动，有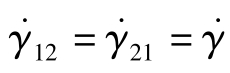，其余项都为零，得到

整理上式，得到

即

在工程计算中，式(5.2.2)和式(5.2.13)有重要的作用，可以计算管内、轴向环隙、平行板间，锥-板间的等稳定简单截面流道流体流动的剪切应力和黏度。在稳态剪切流动中，黏弹性流体应力张量可表示为

(3)不可压缩黏弹性流体的3个流变状态方程

当出现法向应力效应时，应力张量的对角分量，即法向应力分量已不相等，产生法向应力差N₁和N₂。将第3.1节法向应力差函数式(3.1.44)和式(3.1.45)用应变速率来表示，得到判别不可压缩黏弹性流体流变特性的3个流变状态方程

式中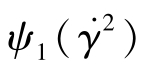，和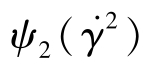分别为第一、第二法向应力差系数。

在工程实际中，广义牛顿流体的黏度与应变速率张量或第二不变量的数学描述，常用一些经验的表达式。需要注意的是即使是同一个本构方程，由于也有不同的数学表达式，实质是一样的。下面简介一些常用的本构模型，包括幂律模型、Ellis模型、Carreau模型、Cross模型、Bingham模型、Herschel-Bulkley模型、Herschel-Bulkley-Arrhenius (HBA)模型等。

(1)幂律模型

Oatwald和De Waele提出的幂律模型(Power law)是经验的。在双对数坐标上，用η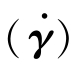作图，就能理解它的由来。图5.2.1给出180℃聚氯乙烯黏度随剪切应力的变化^[5]。如图中所示，在剪切速率的(10^－1~10) s^－1范围内，直线提供的函数为

式中，K为稠度，n为幂律指数，也称为非牛顿指数或流动指数。

将式(5.2.17)和式(5.2.12)代入式(5.2.2)，得到用两参数表示的幂律本构方程剪切应力的表达式

式中，K为稠度系数，表示在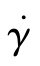＝1s^－1的黏度。它是温度的函数，服从Arrheniu型的关系，有

式中，K₀为T₀的K值，ΔE_τ为恒定剪切应力下的黏流活化能。

① 对于牛顿流体，幂律指数n＝1，K＝μ；

② 对于膨胀性流体，n>1；

③ 对于假塑性流体，n<1，大多数聚合物熔体属于假塑性，其n在0.2~0.7之间；在一定的温度和剪切速率范围内，才有恒定的n，由下式确定

使用毛细管流变仪测试了硬聚氯乙烯剪切应力随剪切速率的变化，如图5.2.2所示。硬聚氯乙烯的配方是PVC树脂(XJ-5)100，三盐4，硬脂酸盐(Ca，Cd和Pb)1.5，Hst/PEl蜡(3/1)1，MBS环氧脂2。用此图按照式(5.2.20)计算流动指数n，列入表5.2.1中。可见流动指数n随加工温度和剪切速率变化。

图5.2.1 180℃聚氯乙烯黏度随剪切应力的变化^[8]

1—相对分子质量分布窄 2—相对分子质量分布宽

图5.2.2 硬PVC剪切应力随剪切速率的变化^[8]

表5.2.1 硬PVC的流动指数^[7]

幂律方程可写成以下形式

式中，ϕ为流动度，它与稠度系数的关系K＝ϕ^－1/m；m为流动指数，m＝1/n，对于牛顿流体m＝1，膨胀性流体m<1，假塑性流体m>1。(www.xing528.com)

幂律模型突出优点是模型简单、使用比较方便，在分析简单截面流道聚合物流体流动中，使用幂律模型，可以解析求解流体流动的控制方程。在早期计算中等剪切速率范围流场中得到广泛的使用。很遗憾的是，它不能用于描述很低和很高剪切速率的聚合物流体，得不到黏性流体真实的流变特性，或者得到错误的流变特性。这是幂律模型的最大缺点。随着聚合物材料和加工成型方法的发展，发展了多参数模型以克服幂律模型的缺点。

(2) Ellis模型

Ellis模型是一个含有3个参数的模型^[2,3]，显然不如幂律模型使用方便。但是，可以预测低剪切速率时流体的牛顿特性。Ellis提出用剪切应力表达物料黏度的表达式^[2]

式中，η₀为零剪切黏度；τ_1/2为η＝η_0/2处的剪切应力的值；α为η＝log(η₀/η－1)对log(τ/τ_1/2)作图的斜率；。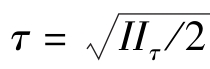

Macosko^[3]给出了Ellis模型另外一种表达式

(3) Carreau模型

为了反映高剪切速率下材料的假塑性行为，又反映低剪切速率下出现的牛顿性行为，可使用Yasuda 1981年提出的5参数描述材料黏度的变化规律的模型^[3]

式中，η₀为零剪切黏度；η_∞为无限剪切速率黏度，即趋于非常大时，聚合物剪切变稀达到的另一个平衡黏度；λ为松弛时间，近似代表剪切变稀开始时剪切速率的倒数；n为幂律指数。

如果取α＝2，式(5.2.23)化简为Carreau的4参数模型^[2,3]

大多数聚合物流体是假塑性流体，η_∞可以假定是零，上式还可简化3参数Carreau模型，有

Polyflow软件给出了这个模型，该模型便于使用，最大的优点是可以成功地预测非牛顿流体的黏度。

给出该方程的另外一种形式

式中，a，b，c为3个待定参数，可通过与实验曲线的对比加以确定。

讨论式(5.2.26)的3种特例，有

① 当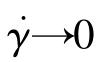，η＝η₀＝a；

② 当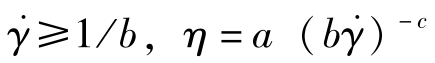，可通过确定幂律指数n来确定c；

③ 当，反映了材料性质由线性区向幂律区的过渡。

可见，Carreau模型多了几个参数，比幂律模型复杂。但是，Carreau模型可以描述比幂律模更广剪切速率范围材料的流动性质。

(4) Cross模型^[3]

在低剪切速率和高剪切速率下，为了描述牛顿区域黏性流体的流变行为，全面描述反“S”形流动曲线所反映的材料流动的转折，1965年，Cross提出以下方程

式中，，4个材料参数η，η_∞，K，n。

分析上式可知，当η₀≫η_∞，即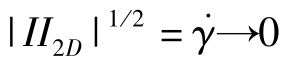，有η→η₀，有η→η₀。在Cross模型区中间有一个幂律模型区域。Cross模型为

分析上式可知，

① 当η₀≫η_∞，上式变为，有η→η₀，即零剪切黏度，为第一牛顿区；

② 在高剪切速率范围，有η→η_∞，即无穷剪切黏度，为第二牛顿区；

③ 中间区域描写假塑性流体规律，参数n反映材料非牛顿性的强弱。

对于大多数聚合物流体，尤其是聚合物熔体，当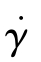增大到一定程度时，大分子链容易发生断裂，不会出现流变曲线的第二黏度平台，η_∞为零，α＝1，式(5.2.23)可化为Cross-Williamsonmoxing模型

Cross模型和Carreau模型一样都是经验模型，物理意义不明确。Cross模型和Carreau模型比幂律模型更全面描述聚合物流体黏性变化的规律。但是，由于参数多，使用不如幂律模型方便。它们都不能描述聚合物流体的弹性行为。必须强调注意的是，在低剪切速率和高剪切速率的情况下，不能使用幂律模型描述聚合物材料加工成型设备流道聚合物流体流动。因为，聚合物加工成型过程中，设备流道里流体的低剪切速率、中剪切速率和高剪切速率同时存在。

(5) Bingham模型（宾汉）^[2，3]

第4.1.2.1节介绍了宾汉流体，即塑性流体。当τ<τ_y时，宾汉塑性材料表现出线性弹性响应，只发生虎克变形。而当τ>τ_y时，材料变为液体，发生线性黏性流动，其黏度成为塑性黏度。宾汉流体的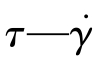曲线是一条不过坐标原点的直线，该直线与纵坐标轴交于屈服应力τ_y，公式(4.1.3)为

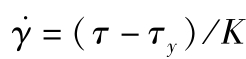，当τ>τ_y

Tadmor^[2]给出了Bingham的一维模型表达式

Macosko^[3]给出了Bingham的一维模型另外一种表达式

1982年，Bird等指出，宾汉模型已被应用于各种各样的流动问题^[3]。

(6)Herschel-Bulkley (HB)模型^[9]

式中，τ_y为屈服应力，Pa；η₀为零剪切黏度，Pa·s；为临界剪切速率，s^－1；n为非牛顿指数（幂律指数）。

此模型最大优点是可预测屈服极限的聚合物流动性质。在低剪切速率和高剪切速率的工程加工中，使用Herschel-Bulkley模型描述非牛顿流体的流动非常成功。

(7)Herschel-Bulkley-Arrhenius (HBA)模型^[9]

在数值模拟的Polyflow商业软件中，给出了含温度变量的本构模型。用Herschel-Bulkley本构方程和近似Arrhenius公式的乘积，来描述物料的黏度η与剪切速率和温度T的关系，有

式中，τ_y为屈服应力，Pa；η₀为零剪切黏度，Pa·s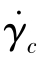；为临界剪切速率，s^－1；n为非牛顿指数（幂律指数）；β为热敏系数，K^－1；T₀为参考温度，即测试温度，K；T为任意温度，K。

HBA模型的最大优点是分段考虑了剪切速率低于零阶剪切速率和高于零阶剪切速率的影响。当剪切速率大于临界剪切速率使用一个公式，当剪切速率小于临界剪切速率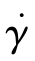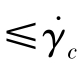使用另外一个公式。使用该模型模拟黏弹性流体的流动特性，取得了非常好的结果。当不考虑温度影响时，式(5.2.31)退化为等温HB模型式(5.2.30)。

由于含温度变量HBA和退化等温HB的本构模型包涵的参数多，最大的优点是可以描述各种非牛顿流体的流变特性。但是，由于它是非线性方程，不能解析求解方程中含有的参数，只能数值求解模型方程的模型参数。还可用Power模型或Carreau模型和近似Arrhenius式的乘积组成描述黏性流体表观黏度的非等温本构方程。在第9章将给出Cross，Carreau和HBA等模型的使用实例。