聚合物材料加工成型时，温度是重要的加工条件之一。聚合物材料的黏度像一般液体那样，是随温度的变化而变化的。但是，聚合物的变化情况是不相同的。目前，已提出一些关于聚合物的黏度-温度关系理论，不同的理论对流动机理的看法不同，得到的黏度-温度关系也不同。
本小节介绍黏度-温度关系的理论，分析温度对流体黏度的影响，包括绝对反应速率理论、自由体积理论、现代理论、黏流活化能、WLF方程的常数值5部分。
绝对反应速率理论又称为过渡状态理论，或活化理论。绝对反应速率理论认为，反应物分子要变成产物，总要经过足够的能量碰撞，先形成高位能的活化络合物，活化络合物再分解为产物，也可分解为原始反应物，并迅速达到平衡，其表达式为
上式，A、B为原始反应物；X#为活化络合物；K#、Ki为反应速率常数；D为产物。
流体的流动与式(4.3.1)有些相似。该理论认为：“在流体流动过程中，当一个分子运动单元从一平衡位置跃迁到下一平衡位置时，需具有一定能量，以克服周围分子对它的作用”[8]。根据该理论，流体流动时的黏度-温度关系可用Arrhenius-Frekel-Eyring(AFE)方程表示为
式子，η为流体的黏度；B为常数；R为气体常数；T为热力学温度；E为黏流活化能。
AFE方程表明，流体的黏度与温度和黏流活化能有关。流体的温度越高，其黏度越小；流体的黏流活化能越大，其黏度越大。这些结论与实验结果相符。对牛顿液体和聚合物流体而言，当温度远高于玻璃化温度或熔点时，黏度与温度的关系服从AFE方程。
图4.3.1为热塑性聚合物熔体黏度随温度变化的曲线。由图4.3.1可看出，图中聚合物的黏度都随温度的升高而降低。但是，黏度降低的程度是不相同的，有些聚合物材料对温度敏感些，有些聚合物材料对温度不敏感。黏流活化能大的聚合物比黏流活化能小的聚合物对温度敏感。例如，PS的黏流活化能E为94kJ/mol，HDPE的E约为24kJ/mol，当将两种聚合物从473K加热到483K时PS的流动度提高了66%，而HDPE的流动度仅提高了17%。由此可知，黏流活化能E大的聚合物只要不超过分解温度，增加加工温度都会提高聚合物材料的流动性。但是，E小的聚合物材料，随着温度的增加，其流动性的增加不大。所以不能用增加温度的办法提高其流动性。
图4.3.1 几种聚合物熔体黏度随温度的变化
自由体积理论认为，由于在流体中存在自由体积，所以流体才具有流动性。所谓自由体积νf是指流体的比容ν与物质分子所占比容ν0之差值，即
1931年，Batchinski第一次提出自由体积理论，同时提出下述简单方程
式中，为η－1流体的流动度；其他符号意义同前。
由式(4.3.4)可看出，η－1与νf成正比，也就是说，聚合物流体的黏度与流体中的自由体积成反比。聚合物流体的自由体积越大，其黏度越小，流动性越好；聚合物流体的自由体积越小，黏度越大，流动性越差。
Doolittle[25]研究了烷烃CnH2n+2指出，可用方程表示黏度与自由体积的关系，为
式中，η为黏度，A′和B为常数，其他符号意义同前。
实验已经证实，自由体积νf的大小与温度有关，用下式表示它与温度的关系
式中，Tg为聚合物的玻璃化温度；T为实验温度；νfg为T＝Tg的自由体积值；α0为自由体积的热膨胀系数。
流体的比容ν与温度有下述关系
式中，αl为流体的热膨胀系数，νg为流体在Tg时的比容，其他符号意义同前。
将式(4.3.3)、式(4.3.6)和式(4.3.7)分别代入式(4.3.5)，整理化简，则可得著名的Williams-Landel-Ferry方程，简称WLF方程
其中
式中，η为温度T的黏度；ηg为温度Tg的黏度；T为绝对温度；Tg为聚合物的玻璃化温度；C1g为常数；B0为常数；C2g为常数，
。
该WLF方程适用的温度范围为Tg<T<Tg+100℃。由此可知，在靠近玻璃化温度Tg区，聚合物体系的黏度可用WLF方程来描述，而当温度远大于Tg时，可用AFE方程描述聚合物体系的黏度。
现代理论[8]认为，在流动过程中，当一分子运动单元从一平衡位置转移到下一平衡位置时，必须克服一定的位能势垒。聚合物流体流动发生需要具备以下3个条件:
① 分子运动单元必须具有足够的能量；
② 在靠近原平衡位置处必须存在一些自由空间——“空穴”，这些自由“空穴”就是分子运动单元新的平衡位置；
③ 必须具有几个分子结构运动单元同时产生变换平衡位置的条件。
由此可知，现代理论统一了绝对反应速率理论和自由体积理论，把它们融为了一个整体。根据现代理论，可用下式表示聚合物的黏度-温度关系
式中，Eν为定容的活化能；A、B为常数；其他符号的意义同前。
现代理论可以较好地解释实验中的黏度—温度关系。因为，不同的聚合物具有不同的性能和结构，从而使其具有不同的黏流活化能和自由体积。故对温度有不同程度的敏感性，所以出现了不同聚合物黏度—温度关系。
在此需要强调指出，聚合物流动时的黏度—温度关系也存在反常情况。即当温度升高时，其黏度不但不降低，反而升高，例如，聚苯乙烯与环己烯所形成溶液的黏度—温度关系，以及聚-2-羟乙基丙烯酸酯与尿素水溶液的黏度—温度关系都属于这种情况。通常认为，这种反常现象是由特殊的分子间相互作用力引起的。也就是说，在靠近相分离温度，或靠近溶液的临界温度，它们从真正的溶液转变成胶态溶液（凝胶）引起大分子间相互作用力的增加，致使黏度升高，流动性降低。(www.xing528.com)
黏流活化能也称为流动活化能。对式(4.3.2)取对数，可得到
该式指出黏流活化能可通过以黏度lnη和温度的倒数T－1为坐标直线的斜率确定，详见图4.3.2。如果lnη—T－1关系不是一条直线，说明黏流活化能是温度的函数。WLF方程指出，由式(4.3.2)定义的黏流活化能必定依赖于温度，即黏流活化能不是常数。这已被观察到，在某一特定温度下，聚氯乙烯E值出现突变，这意味着在这个温度下，出现了结构的变化，从而导致研究新的流动机理。
实验[26]已证实，非牛顿流体黏流活化能不仅依赖于温度，而且依赖于剪切应力和剪切速率。图4.3.3为恒剪切速率和恒剪切应力的顺丁橡胶表观黏度随温度的变化。
图4.3.2 黏度lnη随温度的倒数T－1的变化
图4.3.3 恒剪切速率和恒剪切应力下顺丁橡胶的表观黏度随温度倒数T－1的变化[26]
从图4.3.3中求得，在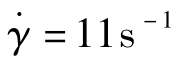
时，恒剪切速率下的黏流活化能
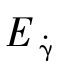＝9.6×103J/mol；在τ＝3×105Pa时，恒剪切应力下的黏流活化能Eτ＝2.8×104J/mol。由此可见，Eτ与
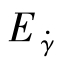是不同的，Bestul和Belcher已从理论上证明
式中，n为流动指数。
在研讨聚合物的黏度与温度之间的关系时，必须具体说明是在恒剪切应力还是在恒剪切速率条件下。对于牛顿体，n＝1，所以Eτ＝
，即牛顿流体的黏流活化能与剪切应力和剪切速率无关。对于大量的聚合物熔体和浓溶液，1/n＝3.5。因此，Eτ＝
。
温度和剪切应力都是外部因素，黏流活化能除了与剪切速率、剪切应力、温度有关外，还与聚合物分子结构参数、填充的补强剂等有关。表4.3.1给出常见聚合物的黏流活化能。
表4.3.1 常见聚合物的黏流活化能[19]
WLF方程及其常数不仅确定着聚合物的黏度—温度关系，而且确定着聚合物黏弹性的其他特性。Ferry[27]指出，就聚合物的大量基团而言，当玻璃化温度被选为参比温度时，WLF方程的常数C1g＝－17.44和C2g＝51.6。WLF方程则变成下列形式
实验指出，方程式(4.3.13)的C1g和C2g的值实为平均值，实际上对不同的聚合物，C1g和C2g值是不相同的，表4.3.2给出部分聚合物C1g和C2g值。
表4.3.2 部分聚合物的C1g和C2g值[27]
由表4.3.2可知，要想使每一聚合物的黏度实验值与计算值一致，WLF方程中的C1g和C2g值就必须采用每一聚合物的实际值，否则会带来较大误差。
上面已指出，方程式(4.3.13)适用于WLF方程的温度范围为Tg<T<Tg+100℃的。但是，这一温度范围并不具有很大的适用性。如聚乙烯的Tg≈－100℃，在室温下使用。故上式用起来有一定的局限。为此，常将WLF方程中Tg改变成TS，这样较适用TS＝Tg+50℃。但是，也要相应改变方程中的常数。经这样的改变，方程式(4.3.13)变成如下形式
实例4.1为了计算C1g和C2g，就需知道的其他常数值。通常假定，在玻璃化温度时，由于自由体积的增加引起聚合物膨胀的产生，有
将式(4.3.6)和式(4.3.7)代入式(1)，化简得
式中，fg为玻璃化温度时聚合物自由体积的体积分数。
由前面得到式(4.3.9)
将式(2)代入式(4.3.9)，有
由大量试验得知
将式(4)代入式(3)，得
所以
若取
C 1 g ＝－17.44
则得
这一结果说明，在玻璃化温度时，各种不同的聚合物具有相同的自由体积分数fg，其自由体积只占总体积的2.5%。也就是说，在玻璃化温度Tg时，可将聚合物看作等自由体积状态。在玻璃化温度Tg时，聚合物ηg也差不多一样，即ηg＝106MPa·s。所以，把玻璃化转变看作是“等黏态”。将其看作等自由体积状态更合理些。这是因为对足够大相对分子质量的聚合物，其Tg与相对分子质量无关，而其黏度强烈地依赖于相对分子质量。因此各种不同相对分子质量聚合物的玻璃化转变温度范围不是它们的“等黏度”范围。由前面可知
α 0＝1/C2g，若取C2g＝51.6，所以
得到
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
