聚合物相对分子质量及分布对流体黏度的影响

聚合物材料包含有大量不同长度的链，每个链包含有一系列单体单元，某一部分聚合物链的运动必将影响其他部分的运动。在加工设备和工艺条件确定后，聚合物熔体的黏度受聚合物的相对分子质量、相对分子质量分布和支化度等分子参数的影响。聚合物领域多年实践经验已证明，聚合物材料的流变性与聚合物相对分子质量、相对分子质量分布和长链支化度有关。聚合物流变性的主要指标是聚合物的黏度η，很多专著^[7]，[8]详细论述黏度η与相对分子质量M_r间的关系。

本小节仅从聚合物流变性能方面介绍聚合物相对分子质量对流体黏性的影响，包括聚合物相对分子质量对流体黏度的影响、聚合物相对分子质量分布对流体黏度的影响两部分。

通常用Mark-Houwink-Sakurada方程，描述[η]与M_r间的关系，为

式中，[η]为聚合物的特性黏度；K和α为已知聚合物-溶剂的经验特征常数。

对于柔性链聚合物，0.5<α<1。对于刚性链聚合物（棒状聚合物），α可以大于1。现已发现，K和α与已知相对分子质量样品的标定方法无关，也就是说，根据测得的聚合物的黏度[η]通过方程(4.2.1)可确定聚合物的相对分子质量M_r。

将方程(4.2.1)应用于θ溶剂(thөta-solvent)的溶液中，在此特殊情况下，假定方程(4.2.1)具有下列简单形式

式中，K_θ为在溶剂θ中测定[η]时的常数K；在这种情况下，α＝0.5。

目前，对于大量不同聚合物-溶剂对，K_θ和α的值是已知的，因此应用方程式(4.2.2)是表征聚合物[η]与M_r关系最简单和最方便的方法。

[η]与M_r间的关系还有一些其他的经验方程，下列经验公式就是其中之一。

式中，A₁和A₂均为常数，A₁接近于。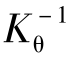

方程(4.2.3)与方程(4.2.1)相比，前者的主要优点为，将方程(4.2.3)中的[η]与M_r之关系绘于[η]与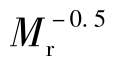坐标上，比绘于lg[η]和lgM_r坐标上，在很宽的相对分子质量范围内，尤其是低相对分子质量范围内为一直线。

Fox和Flory^[7]研究聚合物熔体和浓溶液的[η]与M_r之间的关系，首先得出了经验方程。每一同系列聚合物通过临界相对分子质量M_r，c区分为两个相对分子质量范围。在此两个相对分子质量范围中，η₀和M_r间的关系可用指数定律描述，为

式中，η₀(M_r)为聚合物的零剪切黏度(Initial viscosity)；a和b为同系列聚合物的特殊常数；α的值为1，通常>1；β接近3.4~3.5；如图4.2.1所示。

图4.2.1 零剪切黏度随相对分子质量的变化^[7]

当测得的a值较大时，就无法实现聚合物的真正分子流动。例如，聚氯乙烯就有这样的特性，当t<220℃时，它易于形成稳定的聚集态流体，当其流动时，聚集态流体仍然保持不变。当形成强的分子间键时，比如说，当形成氢键、通过金属离子形成包含酸性基团的交联链时，或者当聚合物链的官能端基有相互作用时，都可观察到这一现象。

一般认为，剪切力的基本作用是破坏链缠结而形成的分子相互作用。由于链缠结是分子尺寸和数量的函数。因此，影响聚合物材料黏度的决定因素是相对分子质量和相对分子质量的分布。

在极低的剪切速率下，多数聚合物溶液和熔体的黏度与剪切速率无关。当剪切速率升高，黏度降低，小于零切黏度值η₀。聚合物浓溶液和线性聚合物溶体的零剪切黏度η₀与相对分子质量有关。低于临界相对分子质量M_r，c时，η₀与相对分子质量呈线性比例关系；大于临界相对分子质量M_r，c时，η₀与相对分子质量3.4次方成正比。

临界相对分子质量M_r，c对应于一定的数值，超过这一数值后，分子缠结的量多到足以阻碍流动，开始控制流动阻力。对于聚合物溶液，即在聚合物中加入溶剂，方程式(4.2.4)中的a、b和M_r，c值均要改变。若式(4.2.4)中，M用重均相对分子质量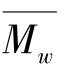代替，式(4.2.4)可用于不同相对分子质量分布的聚合物。

以流变学的观点来看，临界相对分子质量M_r，c可被看作是一个材料常数，表示出现非牛顿流动的低限相对分子质量。非牛顿行为的开始强烈依赖于相对分子质量和相对分子质量的分布。图4.2.2给出不同剪切速率、190℃的线性聚乙烯熔体黏度随相对分子质量的变化。文献^[7]提出，在M_r，c以上，非牛顿行为的起点，随着相对分子质量的增加而出现在较低的剪切速率，详见图4.2.2。

图4.2.2 不同的剪切速率s^－1，190℃的线性聚乙烯熔体黏度随相对分子质量的变化^[7]

(1) 1 (2) 10 (3) 100 (4) 1000 (5) 10000

分子缠结是分子相邻链间的暂时结合。当聚合物相对分子质量超过临界相对分子质量M_r，c后，分子缠结的量多到足以阻碍流动，其黏度才会具有剪切依赖性。实际上，当相对分子质量超过临界相对分子质量M_r，c后，聚合物体系的一系列性质也产生变化。所以，一种化合物只有达到了临界相对分子质量M_r，c后，才可将其归为聚合物一类。某些聚合物的临界相对分子质量如表4.2.1所示。

表4.2.1 某些聚合物的临界相对分子质量(www.xing528.com)

可用经验方程^[10]计算聚合物的临界相对分子质量M_r，c为

式中，K_θ为式(4.2.2)中的常数值，cm³·mol^1/2/g^3/2。

在θ溶液中，K_θ表示聚合物为无限稀溶液的行为。但是，需强调指出的是，用方程式(4.2.5)计算出的M_r，c值仅是近似值。因为甚至对简单的聚合物，用方程式(4.2.5)所计算出的M_r，c也与文献中的实验数据稍有不同。有时根据同一实验所得的M_r，c也不同，这是由于由η₀—M_r曲线从低部分向高部分过度扩大所造成的。

综上所述，在M_r(M_w)>M_r，c以上，聚合物熔体和浓溶液的黏度随相对分子质量的3.4~3.5次方关系急剧升高。这个事实说明，在聚合物加工成型过程中，由于过高相对分子质量物料流动温度非常高，以致使加工变得十分困难。为了降低黏度需要提高温度，又受到聚合物热稳定性的限制。因此，虽然提高聚合物的相对分子质量在一定程度提高加工制品的物理机械性能。但是，不适宜的加工条件又反而会降低制品质量。所以针对制品不同用途和不同加工方法，选择适当相对分子质量的聚合物对加工成型来说是十分重要的。实际上，为了改善聚合物的加工性能，常采用降低聚合物相对分子质量的方法，如聚合物辊压。在聚合物中，加入溶剂或增塑剂等低相对分子质量的物质，以减少聚合物的黏度。

最后，需要再三强调，高聚物材料的黏度和相对分子质量的关系，可用指数等于3.5的指数定律描述，这无疑与聚合物材料的共同运动有关。

聚合物的相对分子质量分布(MWD或MMD)影响其黏度。对相对分子质量分布，通常所称的分散性有多种定义方法。最流行的定义是重均相对分子质量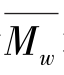和数均相对分子质量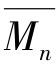之比，即

实验证明，相对分子质量相同相对分子质量分布不同的聚合物，它们的黏度随剪切速率变化的幅度是不同的。图4.2.3给出两种相对分子质量分布的橡胶熔体黏度随剪切速率的变化。由图4.2.3可见，当剪切速率变化小时，相对分子质量分布宽物料的黏度比相对分子质量分布窄的高；当剪切速率高时，发生相反的变化，相对分子质量分布宽物料黏度反而比相对分子质量分布窄的小。在相对分子质量分布比较宽的聚合物中，有一些分子特别长，另一些又比较短，在剪切速率增大时，长的那一部分分子变形较大，对黏度下降的贡献就较多。而相对分子质量比较均一的分子，黏度的变化就比较小。

图4.2.4给出高密度聚乙烯的参比黏度η/η₀随松弛时间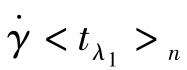的变化。图中所示两种聚合物样品的差别在于相对分子质量分布。样品A是窄分子质量分布，样品B是宽分子质量分布。可见样品B的熔体黏度低于样品A。不少研究得到类似结果。

图4.2.3 两种相对分子质量分布的橡胶熔体黏度随剪切速率的变化

1—相对分子质量分布宽 2—相对分子质量分布窄

图4.2.4 高密度聚乙烯的参比黏度η/η₀随的变化^[7]

相对分子质量分布：A—16，B—84

更确切的说，相对分子质量分布宽的聚合物对剪切速率变化比较敏感，在较高的剪切速率下黏度降低很多。在实际生产中，一般模塑加工的剪切速率都比较高。在此条件下，单级分或相对分子质量分布窄的聚合物黏度比一般分布或相对分子质量分布宽的聚合物黏度大。因此，一般分布或相对分子质量分布宽的聚合物比相对分子质量分布窄的聚合物更容易挤出或模塑加工。

通过方程式(4.2.4)可计算单分散性聚合物的黏度η₀。那么方程式(4.2.4)能否计算多分散性聚合物的黏度呢？研究结果指出，当用相对分子质量大于M_r，c的单分散性聚合物混合时，可用方程式(4.2.4)计算混合物的黏度，计算时以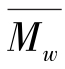代替M_r。有时方程式(4.2.4)中M_r用其他相对分子质量更恰当。例如，聚甲基丙烯酸甲酯采用数均相对分子质量(Number-average molecular mass)更合适些。

如果多分散性聚合物包含有相对分子质量小于M_r，c的分数，其黏度与相对分子质量分布和平均相对分子质量的关系，实际上变得很复杂。在这种情况下，η₀与重均相对分子质量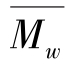间没有简单的关系式。用一个实验来说明，图4.2.5为3种不同相对分子质量聚乙烯与低分子石蜡混合物关系曲线，即牛顿黏度随相对分子质量的变化。在该图中，曲线1~3为和不同相对分子质量聚乙烯和石蜡混合物的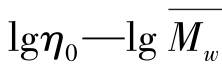实验关系曲线。曲线4是用方程式(4.2.4)绘制出的关系线。

由图4.2.5可看出，由于混合物中有相对分子质量低于M_r，c的分数存在，所以由实验所得黏度值远小于方程式(4.2.4)计算的黏度值。换言之，混合物的黏度不能用方程式(4.2.4)确定重均相对分子质量。在这种情况下，用方程式(4.2.4)计算混合物黏度时的平均相对分子质量可用下式确定

图4.2.5 不同相对分子质量聚乙烯与低分子石蜡混合物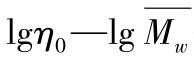关系曲线

式中，M_i为组分的相对分子质量；W_i为混合物质量分数。

与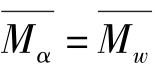和α＝1的情况相反，对于所研究的混合物，当其含有相对分子质量高于和低于M_r，c的分数时，此时α＝0.75。

考虑到相对分子质量分布对黏度η₀的影响，就必须引入不同相对分子质量分布平均数用到相应的计算公式中。这样含有低相对分子质量分数的不同相对分子质量分布的许多聚合物，应用下述经验方程对其进行黏度计算，可得到令人满意的精度。

式中，A₀、A_n和A_w为经验常数，它们依赖于聚合物链的性质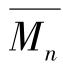；和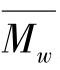分别为数均相对分子质量和重均相对分子质量；α为常数。

α的变化范围较窄，很明显，1/α等于3.5。将大量常数引入上述方程，使它丧失普遍性。但是，对于每种具体同系列聚合物，该方程为计算多分散性聚合物的黏度提供了方便和相当精确的方法。