牛顿流体的流动特点及黏度常数

按照经典流体力学理论，不可压缩理想流体的流动为纯黏性流动。理想的黏性流体，在很小应力作用下流动立即产生，应力停止作用，流动立即停止。但是，黏性变形不能恢复。同时应变不仅是应力的函数，也是时间的函数。如果流动速度不是很大的话，黏性流体的流动是层流，液层是规则的滑移，在液层之间产生速度梯度，流体的层流滑移受到流动的内部摩擦阻力。这种流动的内部摩擦阻力就是黏性阻力，这种流动称为黏性流动。在完全黏性流体中，产生变形消耗的机械功在瞬间以黏性热的形式逸散。

本小节深入介绍牛顿流体的性质，包括黏性剪切流动、牛顿流体的流动特点两部分。

在2.3.2节介绍牛顿黏性定律 (Newton ’s Viscosity Law)。1687年，牛顿第一个对流体简单的剪切运动做了一个著名实验，建立了切向应力和剪切变形之间的关系，得到牛顿黏性公式 (2.3.13)为

式中，μ为流体的动力黏度系数，N·s·m²，即Pa·s。一般简称为黏度系数或黏度。

需要说明的是，牛顿黏性两个公式表示一对大小相等方向相反的剪切应力。为了方便使用三维牛顿黏性公式，使用第2章关于应力正负号的约定。

黏度是流体的一种物理常数，是流体抵抗变形内摩擦的度量。流体的黏度越大，其流动性就越小。黏度可表征流体流动的难易程度。黏度的倒数称为流度。黏度系数μ依赖于流体的性质，它是流体组成、压力和温度的状态函数，与速度梯度无关。

黏度系数的物理意义：促使流体流动产生单位速度梯度的剪切应力。

由此可知，黏度总是和速度相联系，只有当流体流动时才显示出其黏度。

以二维平面流动为例进一步讨论牛顿黏性公式。假设x轴为流动方向，y轴垂直于流动速度u＝dx/dt。显然，位于y+dy流体平面的流速为u+du。位移梯度dx/dy则为剪切应变γ(剪切角速度)，有

剪切应变γ随时间变化的速率称为剪切速率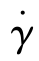，将γ对时间求导数，即

式中，γ上的点表示γ的时间导数。

dγ/dt，du_x/dy这两种表示都是剪切速率，其实质是各层流体的速度在与流动方向垂直方向上的变化率。换句话，也就是单位时间内的剪切应变。将式(2)代入式(2.3.13)，改写牛顿黏性公式，得到牛顿流体的流变方程为

凡是服从牛顿黏性定律简单关系的流体都称为牛顿流体。符合牛顿流动定律的流动，称为牛顿流动。由此式可看出，两层流体间剪切应力（或内摩擦力）与垂直于流动方向的剪切速率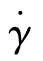(或速度梯度)成正比。(www.xing528.com)

如图4.1.1显示牛顿流体流动过程中应力-应变关系的特点。在应力作用的时间t₂－t₁内，应力引起的总应变可由下式求出

由式(4.1.1)和上式可以看出，牛顿流体的流动具有4个特点。

(1)变形的时间依赖性

当剪切应力一定时，流体的应变随应力作用时间线性地增加，如图4.1.1(a)和(b)所示。牛顿流体的应变是剪切应力和时间的函数，直线的斜率就是应变速率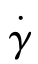，如图4.1.1(b)所示。

图4.1.1 牛顿流体应力-应变关系和黏度对剪切速率的依赖关系

(2)黏度与应变速率无关

在黏性流体流动中，应力与应变速率成正比，如果以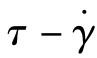作图4.1.1 (c)，可得到一条通过坐标原点的直线，直线的斜率就是牛顿流体的黏度μ。黏度为一常数。如果以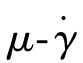作图4.1.1 (d)，可得到一条平行于横轴的直线，这说明牛顿流体的黏度μ是一个常数。黏度μ始终不随剪切速率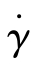而变化。

(3)流体变形的不可恢复性

流体的变形是永久。应力除去后，变形不恢复，而以永久变形保留下来，如图4.1.1 (c)所示。聚合物熔体或浓溶液发生流动后，涉及分子链之间的相对滑移，产生的流体变形是永久的。

(4)能量耗散

在流体流动中，外力对流体所做的功全部以热的形式散失掉。从分子运动角度看，流动是分子质量中心的移动。由于分子间存在相互作用力。因此流体流动过程中，分子之间就会产生反抗分子相对位移的内摩擦力。流体的黏度就是分子间内摩擦力的宏观度量。

曲线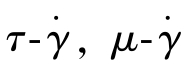和μ-τ统称为流动曲线。它反映了流体的流变性质。