黏性流体传递过程的控制方程组优化

在3.2节建立了用矢量表示的微分形式输运方程和积分形式输运方程，也详细介绍这些流体基本方程组直角坐标系和曲线坐标系中的具体表达。为了后面的章节方便使用已经建立的控制方程，本小节仅汇总了矢量表示的微分形式和积分形式的传递过程的控制方程组。在附录1中详细给出了直角坐标系、柱坐标系和球坐标系的微分形式的控制方程的分量。

本小节汇总传递过程的控制方程，介绍控制方程的基本解法，包括传递过程的控制方程组和控制方程的基本解法两部分。

控制方程组有微分形式和积分形式的流体力学基本方程组，下面分别汇总。

(1)微分形式的流体力学基本方程组

微分形式流体力学基本方程成立的条件是流体流动的物理参数具有连续的一阶偏导数。因此，用理论方法解决流体流动问题最常用的是微分形式控制方程组。下面汇总几种常用的微分控制方程组。前面的章节都介绍了公式中每一项的物理意义和具体的表示，这里不重复。

① 矢量形式。在3.1节中得到本构方程(3.1.29)，在3.2节中分别得到连续性方程(3.2.8a)、运动方程(3.2.18b)、能量方程(3.2.46)和状态方程(3.2.24)，这些方程构成了描述黏性流体流动的矢量形式的控制方程

控制方程组(3.3.1)方程中有12个独立变量u，p，T，ρ，T，其中速度矢量u有3个分量，对称应力张量有6个独立的分量。控制方程中有1个连续性方程、3个运动方程、1个能量方程、1个状态方程共6个方程，最后描述应力张量与变形速度张量的函数关系的本构方程是6个。可见，控制方程包含12个未知数和12个方程，该方程是封闭方程，理论上可以求解。通过前面的分析，可知本构方程可使运动方程转化用变形速度表示的方程；再者如果没有本构方程，能量方程的摩擦热速率Φ与速度变形速度公式(3.2.38a)也无法确定。可见，必须确定聚合物流体的本构方程，才能全面求解聚合物具体的流动问题。

② 非等温不可压缩均质黏性流体流动的控制方程。假设流体为不可压缩流体，即Δ·u＝0，均质流体的状态方程为ρ＝常数，物性参数μ，α也为常数，将运动方程用速率梯度表示，简化方程(3.3.1)，得

③ 非等温不可压缩黏弹性流体流动的控制方程。聚合物加工成型中，流体为黏弹性不可压缩均质的，有ρ为常数和Δ·u＝0，黏度η为常数，用黏弹性流体的本构方程代替式(3.3.2)黏性流体的本构方程，得

式中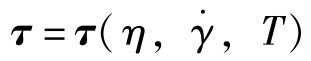，为黏弹性流体的本构方程，η为表观黏度，Pa·s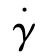；为剪切速率，s^－1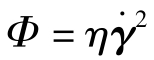；为摩擦热速率。第5章将介绍黏弹性流体的本构方程。

如用应力张量表示运动方程式(3.2.18d)

代入式(3.3.3)，得到控制方程式(3.3.3)的另外一种形式

④ 非稳态非等温不可压缩黏弹性流体流动的控制方程。聚合物材料加工成型过程中，若流体为黏弹性不可压缩均质ρ为常数，流动是层流，即运动方程的u·Δu＝0，略小雷诺数流动，与黏性力相比可忽略质量力；能量方程忽略对流传热项u·ΔT＝0，无内热源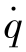和忽略摩擦热速率Ф，简化方程式(3.3.3)，得(www.xing528.com)

该方程组理论上可以求解。先联立求解连续性方程和运动方程，得到了u，p后，再由能量方程求温度场，最后由本构方程确定应力张量的各个分量。可见，必须确定黏弹性流体的本构方程，才能全面求解问题。

⑤ 非等温稳态不可压缩黏弹性流体小雷诺流动的控制方程。聚合物加工成型过程中，大多数机器都是连续运行的，假设设备流道内黏弹性流体的流动是稳态流动，即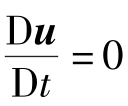；流体流速缓慢，小雷诺数流动，与黏性力相比可忽略质量力，无内热源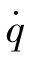，考虑摩擦热速率Φ，简化方程式(3.3.4)，得

⑥ 等温稳态不可压缩黏弹性流体流动的控制方程。在研究聚合物加工成型过程简单截面流道问题中，一般假定等温流动。当然，没有黏性流体是真正的等温流体，因为流体滑动层之间的摩擦产生热量，称为黏性耗散。但是，可以假定窄流道的慢速黏滞流动为等温稳态流动u≠u(T)，不用求解能量方程。黏性力远大于质量力，忽略质量力，稳态黏弹性流体的流动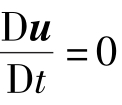。这些假设极大地简化问题，简化方程式(3.3.6)，得到简单的控制方程，为

如用应力张量表示运动方程，得到控制方程式(3.3.7)另一种形式

根据具体求解实际问题的方便，确定使用变形速度表示的控制方程式(3.3.7)，还是应力张量表示的控制方程式(3.3.8)求解问题。

(2)积分形式的流体力学基本方程组

微分形式流体力学基本方程成立的条件是流体流动的物理参数具有连续的一阶偏导数。如果在流体中某局部上出现流体微团的物理参数发生间断现象，在间断面上就不能使用微分形式的运动方程，可以使用积分形式的运动方程，因为在间断面上积分形式方程组仍然成立和正确。积分形式的动量和动量矩方程常被用来研究流体或流体与固体作用的某些总体性质。

求解控制方程组(3.3.1)至方程组(3.3.9)的基本解法有两类，分别是解析法和数值法。这里简述这两种解法^[5]。

(1)解析解法

描述聚合物流变的控制方程都是复杂的非线性二阶偏微分方程，微分形式和积分形式控制方程组都含有二阶偏微分项和非线性项u·Δu和u·ΔT，而且自变量u，T是耦合的，不能独立求解。聚合物工程问题很复杂，必须做出必要合理的假设以简化问题，才能求解控制方程。一般不能直接求解析解。非线性的控制方程组只有在简单特殊情况下才有解析解。但是，在简单特殊情况下，分析聚合物加工成型过程的简化方法是理解加工成型过程的基础。第6章将分析简单截面流道聚合物流体的流动，第7章将分析聚合物典型加工成型过程的流动。针对每一具体问题将给出简化的假设条件，学习如何简化工程问题和求解具体问题的控制方程。

(2)数值解法

差分方法的经典著作于1957年问世，直到有了电子计算机和现代计算技术极大地发展，近似计算方法才得到了广泛应用和发展，求解非线性偏微分方程成为可能。在计算机平台上，使用流体力学计算软件，把工程问题的区域划分成许多微小的网格，在各网格或各小区域中求解流动的控制方程，通过反复计算迭代，提高近似解的精度得到最终解。数值解与解析解本质上是不同的，数值解不能得到在整个区域无限维所有点均能满足的解的表达式，仅能得到区域内网格化后离散节点（有限维）上解的近似值。第9章将介绍数值模拟的解法。