流体的微分型可压缩运动方程式

为使流体流动时呈现连续状态，连续性方程提供了质点速度之间所必须保持的关系。但是，并没有说明在这种关系支配下的质点速度究竟可能包含什么样的运动，流体受到什么样的力。流体的运动方程描述流体的运动形式和力的关系。描述流体运动的第二基本方程是运动方程(Motion Equation)。流体的运动方程是牛顿运动第二定律在流体运动上的表现形式，也称为动量方程(Momentum Equation)。有多种建立运动方程的方法，也有多种形式的运动方程^[1-9]。考虑篇幅和初学者的基础，仅介绍两种方法，给出每种运动方程的形式。

本小节推导建立运动方程，讨论特殊情况下运动方程的简化形式，包括微分型运动方程、特殊情况N-S方程的简化、正交曲线坐标系N-S方程表达式3部分。

介绍用动量定理建立微分型运动方程的两种方法。根据分子间作用力，1827年纳维(Navier)第一次推导出这个方程。在假定剪切应力和法向应力与变形速度为线性关系的假设下，1845年斯托克斯(Stokes)导出该运动微分方程。这里推导这种用应力表示的微分型运动方程。通常称微分运动方程为纳维—斯托克斯方程(Navier-Stokes Equation)，即N-S方程。

(1)将积分型运动方程转化为微分型运动方程

略推导过程，直接给出欧拉型积分动量方程

对上式中ρu进行微分运算，可得

运用式(1)和奥—高公式，将式(3.2.16)中的所有面积分改写为体积分，略去推导过程，得到

即

因为体积dV是任意的，流体连续，即被积函数是连续的，式(2)的积分为零，只有被积函数为零。于是，得到连续介质流体力学微分型的运动方程

即

用张量的注记表示法，上式可表示为

式中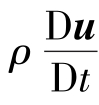，为惯性力，ρg为质量力，divT为表面力。

(2)流体微团的受力分析法

用动量定理分析流体微团的受力推导运动方程。在直角坐标系的流场中，取边长dx，dy，dz的微小平行六面体作为分析对象，流体密度为ρ，六面体质量为ρdxdydz，流速为u (x，y，z，t)＝u_xi+u_yj+u_zk。假设作用于每单位质量流体的质量力为g，它的三个分量为g_x， g_y， g_z。

应力矩阵形式表示式(3.1.22)为

式中，p_xx，p_yy，p_zz为法向应力；τ_xy，τ_yx，τ_yz，τ_zy，τ_xz，τ_zx为剪切应力分量。

由3.1节可知，作用于六面体的表面力如图3.2.5所示，表面应力为

根据动量定理F＝ma，对于任一瞬间，平行六面体内的动量衡算应遵循下式

(流动输出的动量速率)－(流动输入的动量速率)+(累计的动量速率)＝(作用在控制体上诸力之和)

用动量守恒定律可以建立流体流动中流体微团的u，ρ和应力T之间的关系，即可得到应力表示流体的运动方程。这里略去详细推导过程。

图3.2.5 作用于流体微团的各种力

在直角坐标系中，黏性流体微分型运动方程式为

写成一般的表达式，有

式中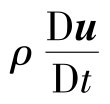，表示单位体积的惯性力；ρg表示单位体积的质量力；Δ·T表示单位体积应力张量的散度。

将式(3.1.33b)T_ij＝－pδ_ij+τ_ij代入式(3.2.18b)，得到直角坐标系用应力项表示的微分型运动方程式^[3,9]

将式(3.1.33a)T＝－pI+τ代入式(3.2.18b)，得到张量表示的微分型运动方程的一般表达式为

在3个运动微分方程式(3.3.18b)至式(3.3.18d)中仅有1个已知量，即质量力ρg。未知变量有速度场u、压力p和表面力divτ＝Δ·τ。独立的未知量有p，u_x，u_y，u_z，τ_xx，τ_yy，τ_zz，τ_xy，τ_yz，τ_xz共10个，可见未知数的个数多于方程个数，需要补充方程。如果补充6个本构方程，给出剪切应力与速度梯度的关系，方程与未知数的数目相等，此方程原则上可以求解。

另外一种方法，利用广义牛顿内摩擦定律，可将微分型运动方程转化为用速度场u表示的流体运动方程。将3.1节得到流体微团剪切应力与剪切变形速度的关系式(3.1.25)和法向应力与有直线变形速度之间的关系式为式(3.1.27b)代入式(3.2.18a)，得到微分型可压缩流运动方程。以x方向为例，得到

同理处理y，z方向，整理得到用速度场u表示的可压缩流体运动方程

对于不可压缩流体，流速场的散度等于零，有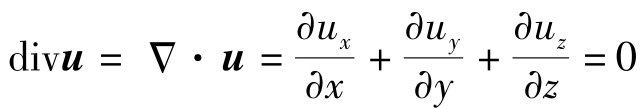，上式右边最后一项为零，速度场u表示的运动方程为

将式(3.2.19a)写成矢量形式的运动方程式，得到以惯性力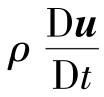、质量力ρg、压力ΔpI、黏性力μΔ²u和流动状态表示的运动微分方程。

对于不可压缩流体，因为Δ·u＝0，所以运动方程式(3.3.20)简化变成

或(www.xing528.com)

式中，ν为运动黏度，ν＝μ/ρ。

将速度的随体导数代入上式，得到

即

式(3.2.22)中的五项很易识别，分别为与时间有关的力，即惯性力、质量力、压力和黏滞力。

在直角坐标系中，不可压缩黏性流体的运动微分方程式写成3个分量形式的方程

或写成以下缩写形式

关联密度、压力和温度的状态方程，对不同热力学假设得到不同方程，有

综上所述，建立流体连续性方程和运动方程依据分别是质量守恒和动量守恒定律。流体流动的方程组共有5个，即连续性方程式(3.2.8)、流体的状态方程式(3.2.24)和N-S方程式(3.2.23)，求解5个未知数速度u_x，u_y，u_z，p，ρ。原则上该问题可以求解。但是，由于N-S方程中有诸如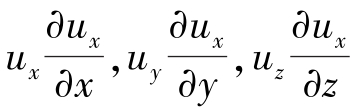等非线性项，在数学上无法求解析解，只有针对某些特殊情况加以简化才能求解。在第6章和第7章中，将结合聚合物工程问题介绍黏性流体运动方程组的求解，讨论这些方程对应所描述的聚合物流体的流动。

N-S流体运动方程组用流速u(x，y，z)＝u_xi+u_yj+u_zk，压力分布p(x，y，z，t)，密度ρ(x，y，z，t)等函数来描述流场。也可清楚看到，方程中的惯性力项是非线性项，不能用解析法求解。在一些特殊情况下可将其简化。这里介绍几种常用的简化运动方程，并且仅介绍如何利用流体的特殊物理性质简化流体运动方程。

(1)欧拉运动方程

对于理想流体，假设流体黏性很小，μ＝0，可忽略黏性力项，则式(3.2.21b)右端的第3项为零，即νΔ²u→0，N-S方程简化得到理想流体运动方程，即欧拉运动方程

或写成另外一种形式

(2)欧拉平衡方程

若是平衡流体，相对于坐标系来说u＝0，欧拉运动方程式(3.2.25a)化简为欧拉平衡方程式

(3)动力压力梯度表示的N-S方程

如流体不具有自由表面，可用动力压力梯度表示N-S方程。因为总压力

p＝p_s+p_d

式中，p_s为静压力，p_d为动力压力。

将上式微分，得到压力梯度为

由静力学平衡方程，有质量力与静压力梯度的关系式

将由式(1)和代入式(2)，得到

将式(3)代入式(3.2.23b)，N-S方程式化简为

例如，在封闭管道中流体流动时，流体不具有自由表面，用式(3.2.26)求解流场比较方便。

(4)小雷诺数流动的运动方程

当物料流速缓慢，因此流体流动的雷诺数Re较小，运动方程中可删除质量力的项。在聚合物加工成型中，熔体流动的黏性力大大大于质量力（惯性力），绝大部分情况下可以忽略质量力（惯性力），运动方程简化为

为了减少流体流动的阻力，工程中大多数设备是圆柱或球形的。因此，在工程中常使用正交曲线坐标，使用N-S方程在正交曲线标的表达式比较方便。用上面介绍的方法读者可以推导在正交曲线坐标系运动方程（动量方程）的表达式。详细的推导读者可参考流体力学有关的文献。下面直接给出柱坐标系和球坐标系中，分别用速度和剪切应力表示的运动方程。

(1)柱坐标系(r，θ，z)的N-S方程表达式

① 速度分量表示的运动方程

(2)球坐标系 (r， φ， θ)的N-S方程^[8]

略，详见附录1公式表的表1.1.3球坐标系运算符和微分型控制方程展开式。

为了使用公式的方便，将常用的公式列入附录1公式表。