连续性方程的推导和表现形式

无数生产实践和科学实验都证明，无论物质经过机械的、物理的、化学的等各种形式的运动，物质的总质量总是不变的，遵循质量守恒定律，同一流体的质量在运动过程中不生不灭。从质量守恒定律(Mass Balance)出发建立连续性方程(Continuing Equation)。描述流体运动的第一个基本方程是连续性方程。在流体为连续介质的假设下，连续性方程是流体运动质量守恒定律的表现形式。

本小节从质量守恒定律出发，介绍几种建立连续性方程的方法^[1-7]，包括积分形式的连续性方程、微分形式的连续性方程、特定条件下的连续性方程3部分。

从质量守恒定律出发建立连续性方程。在宏观运动中，在运动过程中同一流体的质量不生不灭，即

(输出系统的质量流率)＝(输入系统的质量流率)+(系统内质量累积速率)

(1)用拉格朗日法推导连续性方程

对有限体积内的质量运用拉格朗日观点推导连续性方程。在流体微团体积dV内，流体的质量为ρdV，则整个控制体的瞬时总质量式(3.1.15)，为

根据质量守恒定律，在流体宏观运动中，控制体内同一流体的质量不生不灭。控制体内质量的累积速率为

将质量式(3.1.15)代入式(3.2.1)，得到积分型连续性方程为

对式(3.2.2)使用物质体积分的随体导数公式(2.3.39a)，得到积分形式的连续方程

(2)用欧拉法推导连续性方程

运用欧拉观点推导连续性方程，在流场中取任意形状以控制面S为界的一个有限体积为V的控制体，有限控制体的封闭表面积为S，流体密度为ρ，则质量m为流体密度的体积分∭_VρdV。该体积是由空间点组成的，因此它将固定在空间中而不随时间改变，取外法线方向为正方向，n为外法线的单位矢量。任何瞬时连续充满于控制体内的流体质量的变化是经过控制面的流动，由下面两个原因产生：

① 通过控制表面S有流体的流出或流入，单位时间内流出和流入的流体总和为

正号表示总的来说，流体是流出表面S之外的。

② 由于密度场的不定常性，单位时间内体积V的质量将减小，减少的数量为

式中负号表示质量的减少。

考虑体积V内流体质量守恒，单位时间内流出和流入的流体总和等于单位时间内体积V的质量的减小，由此得到

(3)连续方程简化特例

这就是根据质量守恒定律、保持流体呈连续流动状态而得到的连续方程式，它是一切流体运动所必须遵循的一项普遍原则，它有下面两种简化的特例。

① 在定常流动中，流场任何空间点处密度均不随时间变化，因而整个控制体中的质量也不随时间变化，，式(3.2.4)化简为

② 对于不可压缩流体，其密度不随空间和时间发生变化，ρ为常数，式(3.2.4)改写为

在流体流动过程中，因为控制体的位置、形状和体积相对于坐标系不变，式中有

将式(2)代入式(1)，由于密度ρ≠0，最后得到

式(3.2.6)是不可压缩流体的积分型的连续方程式，它适用于定常流动和非定常流动。它的物理意义是，不可压缩流体流动时，任何瞬时流入控制体的流量均等于同一瞬时从控制体流出的流量。

有三种推导微分型连续性方程的方法，下面仅介绍两种方法。

(1)直接将积分公式转化为微分公式

直接将积分形式连续性方程转化为微分形式连续性方程，由式(3.2.3)

用奥高公式将式(3.2.4)中的面积分化为体积分，有，得到

因为流体微团是连续介质，即被积函数连续，体积V为任意的，要使式(3.2.3)和式(3.2.7)积分为零，只能是被积函数为零，分别得到微分形式的连续性方程

矢量形式

矢量形式

式中，为单位体积内由于密度场不定常性引起的质量变化；div(ρu)为流出单位体积表面的流体质量。

由式(3.2.8a)可清楚地看到，式中各项的物理意义：

① 是相对密度变化率；

② divu是相对体积变化率。为了要维持流体微团内质量不灭，必须要求相对密度变化率等于负的相对体积变化率。

可以很容易证明式(3.2.9)是连续性方程式(3.2.8)的另外一种表示形式。因密度的随体导数为

将其代入式(3.2.8)中，为

利用矢量的运算，就得到式(3.2.9a)和式(3.2.9b)

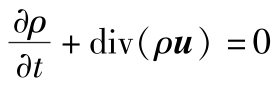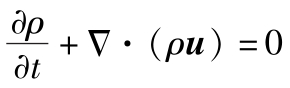和(www.xing528.com)

(2)用欧拉法推导连续性方程

直接对微团体进行质量衡算，也能得到微分形式的连续性方程。在直角坐标系中，取一由空间点组成的固定不动的微团立方体dxdydz，如图3.2.2所示，流体的密度为ρ(x，y，z，t)，任一点的速度为u＝u_xi+u_yj+u_zk，沿各坐标轴的质量通量分别为ρu_x，ρu_y，ρu_z，对微团体进行质量衡算，即

(输出的质量流率)－(输入的质量流率)+(累计的质量流率)＝0

图3.2.2 直角坐标系中质量衡算微团体

分析中略去二阶以上的高阶小量，在x方向通过立方体侧面进入微团体的质量流率为ρu_xdydz，通过侧面流出微团体的质量流率为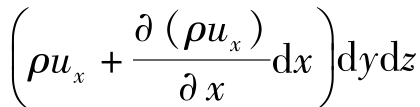，所以在x方向上净质量流率表示为

同理在y，z方向上净质量流率分别为和

于是，得到单位时间内通过微元立方体元6个表面净流出的总质量流量为

考虑控制体内由于密度变化，六面体元中单位时间内流体质量将减少

最后，考虑控制体质量守恒，即流出六面体元外的流体质量应等于六面体元内质量的减少，即式(1)等于式(2)，得

从上式中消去dxdydz化简后，得到直角坐标表系中的连续性方程

展开为

上式中各项的物理意义：

① 为密度的局部导数，或称当地导数，表示密度在空间的一个固定点处随时间t变化；

② 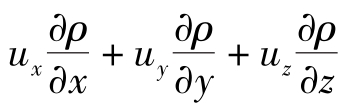为密度的位变导数，表示密度的对流变化，由于流体质量的运动，流体密度由一点移动到另一点时所发生的变化。

用同样的方法，考察柱面体元控制体内流体质量的变化。在柱坐标系中取一由空间点组成的固定不动的柱面体元控制体rdrdθdz，如图3.2.3所示。设流体的密度为ρ(r，θ，z，t)，速度为u＝u_re_r+u_θe_θ+u_ze_z，首先计算通过柱面体元表面的流体质量，进而分别计算单位时间内沿3个坐标方向的净流量。

在坐标轴r方向，单位时间内沿r轴方向的净流量

式中略去了高阶小量。

同理，在θ，z方向，单位时间内沿θ，z轴方向的净流量分别为

将式(1)和式(2)相加，得单位时间内通过柱面体元6个表面净流出的总质量流量为

考虑控制体内密度变化，柱面体元中单位时间内流体质量将减少

最后，考虑控制体质量守恒，即流出柱面体元外的流体质量式(3)应等于柱面体元内质量的减少式(4)，从式中消去rdrdθdz化简整理后，得柱坐标系的连续性方程

对于不可压缩流体，有

使用以上的推导方法，可以推导曲线坐标系中球坐标系的连续性方程。图3.2.4所示的球坐标系中，有

图3.2.3 柱坐标系质量衡算流体微团

图3.2.4 球坐标系质量衡算流体微团

球坐标系中连续性方程的微分式为

对于不可压缩流体，有

在工程实际中存在着一些特殊的情况，流动具有的特殊性，可进一步简化连续性方程式。下面化简已经建立的连续性方程，将式(3.2.8b)和式(3.2.10b)，分别表示为

在流动的特定情况下，可将连续性方程简化为如下几种情况：

(1)定常情况

对于恒定场（稳定场），密度不随时间变化，即ρ≠ρ(t)，有密度的局部导数，连续性方程式(3.2.10a)简化为

或

此式说明，在定常运动时，单位体积流进和流出的质量应相等。

(2)不可压缩流体

不可压缩流体密度等于常数，即ρ为常数，有密度的随体导数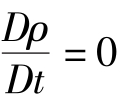，由式(3.2.8a)得到不可压缩流体的连续性方程为divu＝Δ·u＝0，在直角坐标系中，有

此式说明，当ρ＝C时，流体为不可压缩流体，由于流体微团的密度和质量在随体运动中都不变，流体微团的体积膨胀速率（线变形速度）在随体运动中也不发生变化，即Δ·u＝0，即三个方向上线变形速度之和为零，说明了不可压缩流体速度场为无源场。