表述应力与应变关系的本构方程

不同种类的流体其应力和变形的关系不同。可按应力与变形的关系来区分流体的类型。这一节利用流体本身具有黏性这一特性，讨论牛顿性流体应力与变形速度之间的关系，导出应力与变形速度关系的方程——本构方程。建立牛顿流体本构方程的依据是牛顿内摩擦定律。

本小节介绍表述应力与变形关系本构方程的基础知识^[2]，包括应力与变形速度张量的关系、偏应力张量和膨胀黏性系数、正交曲线坐标系的应变速率张量3部分。

这里分别介绍剪切应力、法向应力与变形速度张量的关系。

(1)剪切应力与变形速度张量的关系

由2.3.2节知道，牛顿内摩擦定律二维表达式(2.3.13)为

由3.1.1节流体微团速度的分解得知，由于速度梯度存在，经过dt时间后，原来的矩形流体微团发生剪切变形成为平行四边形，其剪切角为，即速度梯度等于剪切变形的角速度。

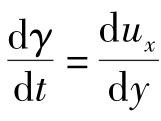牛顿内摩擦定律可改写为

由3.1.1节已知，流体微团一个边的剪切角速度如图3.1.4所示，为

流体微团整体的剪切角速度

图3.1.7 流体微团的剪切变形与切应力

将图3.1.7(a)绕A点旋转成图3.1.7(b)或图3.1.7(c)，则形成与图3.1.4相同的剪切运动形式。将式(2)代入式(1)，再根据Cauchy应力定律得

斯托克斯假设流体各向同性，应力与变形速度成线性关系。将切向应力与角变形率的线性关系推广到三维空间流动，在三个正交平面上得到流体微团剪切应力与剪切应变速度的关系式，即在流体三维运动情况下牛顿内摩擦定律的推广式

按照Tadmor^[10]应力正负号的约定，剪切应力与剪切应变速度的关系式，即牛顿内摩擦定律的推广式为

特别强调，使用本书关于应力正负号的约定，牛顿内摩擦定律的推广式为(3.1.25)。在求解工程问题时，两种约定求解同一问题使用不同的用应力表示的运动方程，得到的解是一样的。前提是在求解一个问题时，自始至终使用一种约定。

(2)法向应力与变形速度张量的关系

流体黏性也阻碍流体微团运动中的直线变形。分析法向应力与直线变形速度之间的关系。当ABCD经过发生dt时间变成如图3.1.7 (a)所示的AB′C′D′时，流体微团单元体在x方向拉长，在x方向的黏性阻力阻止其伸长，反之相反，流体微团单元体在x方向缩短在x方向的黏性阻力阻止其缩短。由于黏性而引起的沿流体微团表面法向作用的应力大小必然与各该方向的直线变形速度有关，而与直线变形的方向相反。因而按照剪切应力与剪切应变速度的关系可以类似地写出，为

由上式可以看出，由于各个方向的直线变形速度不相等，因此黏性阻碍作用所产生的法向应力也是各向不等；统称为一点上的各向异性压强。于是在实际流体运动时，一点上的法向应力除了由于分子运动统计平均的各向同性压强p之外，还需加上由于黏性影响而与直线变形有关的各向异性压强。法向应力由两部分组成：

① 由流体静压力产生，流体微团承受压缩应力，发生体积变形；

② 由流体流动时黏性应力的作用产生，使流体微团在法线方向上承受拉伸或压缩应力，发生线性变形。

最后，可得到法向应力与直线变形速度之间的关系为

式中，附加应力为

对于不可压缩流体，有速度散度为零，即divu＝0，式(3.1.26)简化为

将式(3.1.25)与式(3.1.27b)代入式(3.1.22)，得到应力矩阵，为

即

式(3.1.28a)和式(3.1.28b)就是全面反映各向同性不可压缩牛顿流体应力与变形速度关系的本构方程。

对于可压缩流体，将式(3.1.28b)写成三维应力张量T——本构方程的表达式

应力张量和变形速度张量之间的关系满足牛顿内摩擦定律的流体称为牛顿流体，否则称为非牛顿流体。例如工程中常用的油漆、颜料、橡胶、塑料等为非牛顿流体。实践证明，牛顿内摩擦定律的适用范围远远超出人们所能预料的，它不仅适用于超音速气流，甚至适用于高超音速气流，只有在物理量变化极端剧烈的激波层内，它的适用性才存在问题。

利用张量代数运算，分解应力张量。讨论偏应力张量和膨胀黏性系数。

(1)偏应力张量

若流体微团的应力状态由应力张量T描述，根据力的性质不同，应力张量可以分解为各向同性压力和偏应力张量两部分，有

用注记符号表达上式，有

由上式得到，最常见的一种应力张量T的分解形式为

式中，trT为张量T的迹，I为单位张量；τ为偏应力张量。

若定义

则T分解成

或写成注记符号分量式

式中，p为各向同性压力（静水压力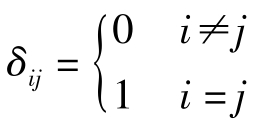）；称为Kroneckerδ，是单位张量I的一种表示法。式(2.2.13)曾给出I的表达式

在任何状态下，牛顿流体内部都具有各向同性压力。它作用在曲面法向上，且沿曲面任何法向的值相等，负号表示压力方向指向封闭曲面的内部。

由分量τ_ij组成的应力张量τ称为应力偏量，或偏应力张量，其值等于全应力张量减去代表均载荷的分量。偏应力张量是应力张量中最重要的部分，直接关系到流体流动、黏性和弹性的变形的描写，是流变学研究的重点。

注意式(3.1.28)定义的各向同性压力－p具有一定的任意性，它并不一定真正等于液体内部的真实静水压力，由此，它将影响到偏应力张量法向分量τ_ii(i＝1,2，3)的值。

下面将证明，偏应力张量中法向分量的绝对值τ_ii并无很大意义，重要的是沿不同方向的法向应力分量的差值，它们对于描述非牛顿流体的弹性行为十分重要。分析式(3.1.33a)，按照Cauchy应力定律，平衡时，物体所受的合外力与合外力矩均等于零。因此可知，全应力张量和它的偏应力张量的剪切分量都是相等的，即

由上两式，得到应力偏量的主要特征，它的第一不变量等于零

当各向同性压力－p按式(3.1.33b)定义时，应力偏量为

平衡时，应力张量中沿主对角线对称的剪切应力应相等。与应力张量相似，偏应力张量也是对称张量，仅有6个独立分量。有偏应力张量的3个法向应力τ_ii(i＝1，2，3)，3个剪切应力分量τ_ij(i，j＝1，2，3)。(www.xing528.com)

下面用几个例题讨论牛顿流体特殊流动的内应力。

例题3.1.6 确定静止液体或流体的内应力。

解：静止液体或流体内只有法向应力，实际上就是各向同性压力，应力张量只有各向同性压力；无剪切应力，即偏应力张量为零张量。由广义形式应力张量为

得到各应力分量为

任何静止的平衡液体，或是静止或流动的无黏流体都处于这种应力状态。

例题3.1.7 设流体流动时只受到一个方向的拉力或压力，除此之外不再有任何其他作用力，由流体应力张量式，确定流体流动时均匀拉伸或压缩的应力。

解：根据该流体流动时的受力状态，分析应力张量T的各应力分量为

此时流体体系处于沿x₁方向的均匀拉伸或压缩状态。τ>0为拉伸，τ<0为压缩。纺丝过程中，在单轴拉伸流场中，材料处于这种应力状态。

例题3.1.8 设流体流动时流体微团仅受到均匀剪应力，由流体应力张量确定流体流动的剪切应力。

解：流体微团仅受到均匀剪切应力，设流体应力只有剪切分量τ₁₂＝τ₂₁＝τ＝常数，而所有其他剪切分量为零。这表示流体体系在x₂等于常数的平面上沿x₁方向受到剪切应力τ₂₁；按剪切应力对等原则，在x₁＝常数的平面上沿x₂方向也有剪切应力τ₁₂存在。这种剪切应力称均匀剪切应力。在许多仪器、设备、模具内的材料流动场中，可用简单剪切流场来分析。

(2)膨胀黏性系数^[2]

当流体运动消失时，τ_ij等于零，它只和流体变形有关。τ_ij＝λε_kkδ_ij+2με_ij，将其代入式(3.1.33b)，有

引进第二黏性系数，即膨胀黏性系数

于是式(1)可写成

需要说明，流体微团所有方向上法应力的平均值等于x，y，x三个方向上法应力的平均值，它是不随坐标系改变的不变量。

对于不可压缩流体divu＝0，通常的液体、低速运动的气体都是不可压缩流体，其平均法应力等于运动流体的压力p，第二黏性系数μ′自动不出现，本构方程中只出现动力黏性系数μ；对于可压缩流体，divu≠0，高速运动的气体是可压缩流体。在运动过程中，液体的体积发生膨胀或收缩，它将引起平均法应力的值发生μ′divu的变化，因此称μ′为膨胀黏性系数。除了高温和高频声波这些极端的情况，对一般情况下运动的气体，斯托克斯提出假设在分子运动理论中得到证实，近似地认为

μ′＝0

对于聚合物流体的流动，由式(3.1.40)得到斯托克斯假设

式(3.1.41)说明流体一点上的各向同性压强也就是不可压缩实际流体中不同方向压强的算术平均值，因此它代表一点上的流体动压强。在平衡流体中，它代表一点上的流体静压强。它作用在曲面法向上，且沿曲面任何法向的值相等，负号表示压力方向指向封闭曲面的内部。

斯托克斯假设给具体计算实际流体中的压强带来很大的方便，无须进一步研究各向异性压强，只要找出各同性压强与其他流动参数之间的关系，则可据此算出各向同性压缩实际运动流体一点上的流体动压强。由此可知，压强p有三种不同的含义：

① 在平衡流体中，代表一点上的流体静压强；

② 在理想流体中，它代表一点上的流体动压强；

③ 在不可压缩实际运动流体中，它代表一点上流体动压强的算术平均值，因此它也代表一点上的流体动压强。

现在考察在简单剪切流场中材料所受的法向应力的情况。这里重点强调牛顿流体与聚合物流体在简单剪切流场中不同的应力状态。

牛顿流体只有黏性而无弹性，因此在应力张量T中与弹性变形联系的各法向应力分量相等，均可归于各向同性压力，T_ii＝－p。而偏应力张量τ_ij中，各法向应力分量等于零，τ_ii＝0。应力张量分解为

由此可见，偏应力张量中只有一个独立分量——剪切应力分量τ，故只需定义一个黏度函数，就可以完全描述其力学状态。

聚合物熔体或液体是黏弹性流体，在剪切场中既有黏性流动又有弹性变形，一般情况下三个坐标轴方向的法向应力分量不相等，τ₁₁≠τ₂₂≠τ₃₃≠0。因此要完整描述聚合物液体的应力状态，偏应力张量τ_ij中至少需要有4个应力分量τ₁₂，τ₁₁，τ₂₂，τ₃₃，有

流变函数除了黏度函数外，还要定义与法向应力分量相关的函数。

偏应力张量中法向应力分量的值与各向同性压力的大小有关。注意到式(3.1.28)给出的各向同性压力的定义有一定任意性，这就使得应力张量的分解方法有多种结果。下面用一例题说明，同一应力张量的有多种分解方法。

例题3.1.9 有一个应力张量，给出两种不同的分解方法。

解：按照张量加法的运算法则，将应力张量分解成两个应力张量的和，有

或者

两种结果中各向同性压力的值不同，由此导致偏应力张量中法向应力分量τ_ii的值不同。用这叠加原理，分析平行平面的相对平行移动产生的简单剪切流动，该稳态剪切流动中，T₁₃＝T₃₁＝0，T₂₃＝T₃₂＝0，黏弹性流体应力张量可表示为

由上式可知，在不可压缩材料中，只有假设各向同性压力才能由应变或应变历史确定出应力状态。可见，应力张量中的任一法向分量的绝对值没有流变意义。但是，法向应力差不会由于任何各向同性压力的加入而改变，主要依靠材料的流变性质。可以看出，不管应力张量如何分解，偏应力张量中两个法向应力分量的差值τ₁₁－τ₂₂，τ₂₂－τ₃₃，始终保持不变。这给予重要的启示，在聚合物液体流变过程中，单独去追求法向应力分量绝对值没有多大意义。于是，定义两个法向应力差函数来描写材料弹性形变行为。

第一法向应力差函数为

第二法向应力差函数为

用N₁、N₂和黏度函数这3个函数就可以完整描写简单剪切流场的聚合物流体的应力状态和黏弹性。

变形速度的数学描写与选择的参考坐标系紧密相关。工程中常使用柱坐标系和球坐标系。读者可以使用第2.4.4节正交曲线坐标系场的变化率一节介绍的拉梅系数和张量运算公式，确定正交曲线坐标系的应力与变形速度梯度关系。这里不详细推导。

由于工程中常用应变速率张量的分量表示剪切应力与变形的关系。因此，这里直接给出切变速率张量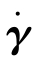不同坐标系的分量公式。

(1)直角坐标系应变速率张量的分量

(2)柱坐标系应变速率张量的分量

(3)球坐标系应变速率张量的分量