力的分类和应力张量详解

本小节简单介绍流体流动时所受的力及其性质。在流体中取一封闭曲面S为界面的体积元V的流体，在控制体上作用的力有两类，一类是作用在体积内所有流体微团上的体积力，如质量力。另一类是控制体外部流体和固体对控制体内流体的作用力，即作用在流体表面的表面力，包含压应力和剪切应力（摩擦阻力）。这些力可能是已知量，也可能是未知量，可能是流体固有的，可能是由于动量变化而产生的。这些力的作用情况有时相当复杂，将在下一章针对具体情况做详细的分析讨论。为了使问题简化，在此只讨论作用在控制体上诸力的积分。

本小节介绍力的分类和二阶应力张量^[2]，包括质量力和表面力、二阶应力张量2部分。

这里分别介绍质量力和表面力的物理意义和数学表达式。

(1)质量力

首先引入密度的定义。

密度的定义 在连续介质中，在流体中取一点M，围绕M点作体积元素ΔV，它的质量为Δm，当ΔV向M点无限收缩，若极限值

存在，则称此极限为流体在M点的密度，以ρ＝ρ(x，y，z，t)表之，kg/m³。密度的物理意义就是单位体积内流体的质量。

由式(1)得出

流体的总质量为式(2)的体积分

可见，质量与密度和体积成正比。

质量力是一种体力。质量力是指作用在所考察的流体整体上的外力。作用在体积V各个流体微团上的力称为质量力。质量力包括直线运动惯性力和离心惯性力。它与流体微团的质量大小有关，并且集中作用在流体微团的质量中心，用同样的方法作用在每个分子上。

质量力用空间的分布密度f表示。在体积V内取一点M，围绕M点作体积元素ΔV，它的质量为Δm，当ΔV向M点无限收缩，若极限值

的极限存在，这极限值f代表M点上单位质量流体所受到的质量力。f＝f(x，y，z，t)是空间坐标和时间的函数，称为在空间中的质量力分布密度函数。由式(3)得到作用在体积元上的质量力为

dF＝ρfdV

积分上式，得到作用在有限体积上的质量力

式中，F为单位质量流体微团所受的质量力。若dV是体积元，F的大小很有限，则作用在dV上的质量力dF是三阶无穷小量，量纲为。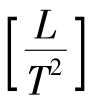

作用在流体微团的质量力包括重力和惯性力。在聚合物流变学中，仅限于考察处于重力场作用下的流体，用重力加速度g代替式(3.1.16)中的f，得到质量力为

式中，g为重力加速度，等于9.81m/s²。

(2)表面力

与界面S接触的流体或固体作用于流体团表面S上的力称为表面力，简称面力T。例如压力、摩擦力都是面力。此种力由与该流体微团毗邻的外部流体而来的，由静压力和黏性力所提供。

面力用表面上的分布密度来表示。在连续介质中，在流体中取一点M，围绕M点作面积元素ΔS，设ΔS的法线方向为n，n所指向的流体或固体作用在ΔS面上的面力为ΔT，当ΔS向M点无限收缩，若极限值

存在，则它代表M点上以n为法线的单位面积上所受的面力，也称为表面力。T_n不仅是x，y，z，t的函数，而且依赖于作用面的方向。一般来说，作用面的方向不同，T_n也不同。T_n被称为面力在S面上的分布密度，或称为应力。由式(3.1.18)作用在dS面上的面力为

积分上式，得到作用在有限面积S上的面力为

显然面力和面积呈正比。若dS是面积元素，T_n的大小有限，则作用在dS上的面力dT是二阶无穷小量，量纲为。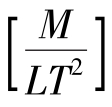

过任一点M可作无数个不同方向的表面，作用在这些不同表面上的面力一般是互不相等的，T_n是矢径r和表面法向单位矢量n两个矢量的函数。从第1章张量的学习中可知，只要知道3个坐标面上的应力，则任一以n为法线方向的表面应力都通过它们和n表示出来，也就是说3个矢量或9个数量分量描述了一点的应力状态，即可用应力张量描述一点的应力状态。

这里介绍二阶应力张力的物理意义和各种数学表达式。

在外力或外力矩作用下，物体会产生流动或（和）形变，同时为抵抗流动或形变，物体内部产生相应的应力。应力通常定义为材料内部单位面积上的响应力，单位为Pa(1Pa＝1N·m^－2)或MPa(1MPa＝10⁶Pa)。在黏性不起作用的平衡流体和理想运动流体中，作用在流体微团表面的表面力只有与表面相垂直的压应力，而且压应力又具有一点上各向同性的性质。也就是说，在流体微团表面上，作用的表面力只有与表面相垂直的压应力（压强）。在平衡状态下，物体所受的外应力与内应力数值相等。在实际流体的运动中，由于流体的黏性，作用在流体微团体上不仅有压应力，而且还有剪切应力。

在黏性流体的流动或形变中，由于黏性的作用，流体微团的平移、旋转和剪切变形运动使流体微团内部存在相互挤压或拉伸和剪切的作用，存在压应力和剪切应力。黏性流体流动时，在流体微团的同一位置，通过面积相等取向不同面元的力也是不相同的。也就是说，作用力与截面的取向有关，用数量无法表示。必须用二阶张量来描述黏性流体流动所受的力。在流变过程中，聚合物液体既有黏性形变又有弹性形变，其内部应力状态相当复杂。要全面描述非牛顿流体内部的黏弹性应力及其变化情形，需要引入应力张量的概念。

如果在流体内某点通过任意取向的单位面积的力能够计算出来，就可以完全清楚该点的相互挤压或拉伸和剪切的作用。下面用例题引入流体应力张量的概念。

例题3.1.4 求解描述黏性流体流动的流体形变应力。

解：在流体内取定一点M，包围M作一个四面体元ABCD，如图3.1.5所示。ABC面取任意方向，其余三面分别垂直于x₁，x₂，x₃轴。规定ABC面以外侧为正，n是它的外法线。其余3个侧面分别以x₁，x₂，x₃轴的正方向为正。设ABC面元矢量dS_n＝dS₁e₁+dS₂e₂+dS₃e₃，则

式中，β_ni为n与x_i轴夹角的余弦。在n与x_i轴呈锐角的情况下，dS_i就是垂直于x_i轴的那个侧面的面积；在呈钝角的情况下，二者有一符号之差。(www.xing528.com)

图3.1.5 四面体元

设矢量T₁，T₂，T₃分别为朝坐标轴正方向通过三个侧面的单位面积的力，T_n为朝n方向通过ABC面单位面积的力。四面体元通过三个侧面所受到的力分别是dS₁T₁，dS₂T₂，dS₃T₃。略去自重等体力比侧面力高一阶的无穷小量。

朝n方向通过面元ABC的力

由四面体元力的平衡条件，由式(2)得

将式(1)代入上式(3)，得

设矢量T₁，T₂，T₃的分量分别为T₁₁，T₁₂，T₁₃；T₂₁，T₂₂，T₂₃；T₃₁，T₃₂，T₃₃，代入式(4)得

由式(3.1.21)可知，通过任意给定取向面元上单位面积的力由上式中的9个数量T_ij确定，即流体形变应力——应力张量为二阶张量。

通过上面的讨论可知，当考察通过黏性流体内任一面元的力时，既要考虑这个面元的方向，还要考虑通过这个面元上力的方向。这种二重取向的特殊性使得这类物理量在三维空间中要用9个数量表示。

在黏性不起作用的平衡流体和理想运动流体中，在流体微团表面上，作用的表面力只有与表面相垂直的压应力（压强）。在实际流体的运动中，由于流体的黏性，作用在流体微团体上不仅有压应力，而且有剪切应力。

例题3.1.5 在实际运动流体的直角坐标系中，确定流体流动应力张量的表达式。

解：在直角坐标系中，取出流体边长dx，dy，dz的六面体微团A(x，y，z)。由于黏性的影响，作用在微元体ABCDEFGH上的表面力就不仅有压应力p，而且也有切应力τ。一点上的压应力也不再具有各向同性的性质。流体微团每个表面上的表面力都有3个分量，共有9个数量。将9个应力分量分别标注在包含A(x，y，z)点在内的三个微元表面上，矩阵T中对角线分量是法向应力，非对角线分量是切向应力，如图3.1.6所示。

图3.1.6 流体微团上的应力

实际流体中—点，A(x，y，z)点上的应力可用9个元素组成的一个应力矩阵，即直角坐标系的二阶应力张量T表示为

广义形式应力矩阵张量T方阵表示式(2.2.9)

式中，应力的第一个下标表示应力作用面的法向方向，第二个下标表示应力的方向。

应力张量 T_ij描述任意一流体微团A(x，y，z)处相互挤压或拉伸和剪切的作用。其中所有T_ii(i＝1,2，3)分量都作用在相应面元的法线方向上，称为应力张量的法向分量。法向力的物理实质是弹性力，即拉力或压力。所有T_ij(i≠j；i，j＝1,2，3)分量都作用在相应面元的切线方向上，称为应力张量的剪切分量。剪切应力的物理实质是黏滞力（内摩擦力）。

这里观察到一个问题，在力学中一般把与各个坐标正向方向的力和加速度作为正的。但是，根据作用力和反作用相等的牛顿定律，必须会想到一个问题。如果在某面的一侧施加了一个力，那么在该面的另一侧也就施加了一个大小相等、方向相反的力。如何约定应力分量的正负号？

特别强调指出，关于应力的正负号，国外聚合物流变学领域的专著使用不同的约定。米德尔曼^[8]应力的正负号约定：在某面正侧的材料向该面负侧的材料施加应力T_ij，如果力的作用力线沿着x_i的正方向，它就是正的；反之，某面负侧的材料向该面正侧的材料施加的应力，如作用线沿着x_i的负方向，这一应力也是正的。如图3.1.6所示，剪切应力都是从3个平面负侧材料产生的，图中指示出的方向是应力各分量的正方向。Macosko^[9]第47页提请读者注意，他的书使用拉伸应力是正的符号约定。其他一些专著，特别是1987年Birder的书中选择张力是负的(tension as negative)。

本书使用米德尔曼^[8]应力的正负号约定。在求解工程问题时，不同应力正负号的约定求解同一问题得到的解是一样的。前提是在求解一个问题时，自始至终使用一种约定。使用中非常容易发生混用的情况，不可能得到正确的解。

还需要注意，dS面法线方向的定义，如果dS是封闭曲面的一部分，则取外法线方向为dS的正方向。如果dS所在的曲面不封闭，则约定取一方向为法线的正方向，法线n指向的那一边流体作用在面上的应力以T_n表之，而位于与n相反方向的流体微团作用于dS面上的应力以－T_n表之。

按Cauchy应力定律，在平衡时，物体所受的合外力与合外力矩等于零。可知，平衡时，应力张量中沿主对角线对称的剪切分量应相等，即

T_ij＝T_ji(i，j＝1，2，3)

此式表明，在物体平衡时，应力张量只有6个独立分量。其中，3个为法向应力分量为T_ii(i＝1，2，3)，3个为剪切应力分量分别为T₁₂＝T₂₁，T₁₃＝T₃₁，T₂₃＝T₃₂。可见，聚合物流变的应力张量是二阶对称张量。因此，它具有对称张量所有的性质：

① 应力张量具有三个互相垂直的主轴方向。在主轴坐标系中，应力张量可写成下列对角线形式

式中，p₁₁，p₂₂，p₃₃称为法向主应力。于是在与主轴方向垂直的面上，只有法向应力。切向应力等于零。

② 应力张量的3个不变量

通过学习可知，在无黏性理想流体流动中，在流体微团表面上，流体表面力只有与表面相垂直的压应力（压强），而且压应力又具有一点上各向同性的性质。令法向应力的共同值以－p表示，则

p ₁₁＝p₂₂＝p₃₃＝－p(x₁，x₂，x₃，t)

p称为理想流体的压强，它是x，y，z，t的函数，压强的方向与作用面的法线方向恰好相反。由此可见，在理想流体中，应力张量变为T＝－pI，只要用一个数量便完全描述任一点的应力状态。理想流体同一点上各个不同方向的法向应力是相等的。

在静止流体中，不论是黏性还是理想流体，根据流体的易流动性，静止的流体不能承受剪切应力，因此同样有T＝－pI，－p代表的是静力学压应力函数，它表征静止流体每一点上的应力状态。