流体运动分类与分解

为了研究问题和建立工程问题数理模型的方便，将流体运动进行分类。流体运动要比刚体复杂，因为它除了平动和转动外，由于流体的易流动性，流体微团还要变形。为了描述流体的复杂运动，需分解流体的复杂运动。

本小节介绍流体运动的分类和流体流动的分解^[2]~[4]，包括流体运动的分类、亥姆霍兹速度分解定理、流体微团运动的三种形式3部分。

在流体力学中，以雷诺数Re(Reynold number)来判别流体流动性质，聚合物流体大多数流动是小雷诺数流动。流体运动有三种分类形式，包括以流体运动的形式为标准分类、以时间为标准进行分类、以空间为标准分类。首先介绍雷诺准数，再介绍流体运动的分类。

在黏性流体的流动中，一般用雷诺数Re判别流体流动的性质。雷诺数Re代表了惯性力与黏性力之比。当Re很小时，可忽略惯性力。以管中流体流动为例，定义雷诺数Re，为

式中，u流体流动的速度，ν为流体运动黏度，d管的直径。

(1)以流体运动的形式为标准分类

设q₁，q₂，q₃三维正交坐标系，流体运动的所有物理量用欧拉法描述，速度场为

若场内物理量不依赖于矢径r则称之为均匀场，反之称之为不均匀场。黏性流体流动中，研究的大多数问题是不均匀场。若在整个流场中，速度旋度为零rotu＝0，则此流动为无旋流动，反之为有旋流动。因为，绝大多数流体运动都具有平动和变形，因此对于这两种运动形式不加分类。于是流体运动以运动形式为标准进行分类，分为无旋流动和有旋流动两种。

如果需要考虑温度的影响，就分别有等温流速场和非等温流速场

(2)以时间为标准进行分类

若场内函数依赖于时间t称为非定常（不稳定）场，如式(3.1.2)所示；反之如式(3.1.3)所示为定常（稳定）场。流体运动以时间为标准进行分类，分为定常场和不定常场两种。

(3)以空间坐标为标准分类

设流场所有有关的物理量依赖于一维正交坐标u＝u(q₁)、二维正交坐标u＝u(q₁，q₂)和三维正交坐标u＝u(q₁，q₂，q₃)的运动，分别称为一维、二维和三维的运动。流体运动以空间坐标分类，分为一维、二维和三维运动3种。

运用流体流动的分类简化实际流体的流动，便于数学上表达求解简化的传递方程组和相应的边界条件。从简单的运动形式着手，研究流体流动的内在规律，在此基础上再进一步处理更复杂的流体流动。在后面章节学习中，要运用分类的方法简化聚合物工程的问题。

从物理学和理论力学中得知，任何一个刚体运动可分解成平动和转动之和，其速度可表示为

式中，u₀是刚体选定点的平动的速度，r是刚体选定点到点O的矢径，ω是刚体围绕定点O转动的瞬时角速度，在同一时刻ω＝rotu/2，将其代入式(3.1.4a)，得到

该式为刚体的速度分解公式。

流体运动要比刚体复杂。由于流体的易流动性，流体微团除了平动和转动外，还要变形。为了描述流体的复杂运动，需将流体的复杂运动分解。

在流场中取流体微团平行六面单元体dxdydz，如图3.1.1所示，设微团质量中心点A(x，y，z)在瞬时的速度为u(x)＝u_xi+u_yj+u_zk，与点A相距极近的C点为C(x+dx，y+dy，z+dz)，在同一瞬时，速度近似式为略去二阶以上C(x+dx，y+dy，z+dz)无穷小量的泰勒公式

图3.1.1 流体微团的单元体

因此，速度梯度张量L的表达式为

用注记符号表示的矩阵分量表达式为

对速度近似式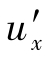作恒等变形，在式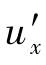的第一项中人为地增加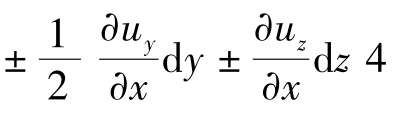项，并将式中的最末两项也改写成带1/2系数的4项，于是式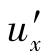变为

按此方法将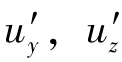写成类似的形式，使用表3.1.1中的符号将速度近似式改写成为

式(3.1.6)是流体微团的速度分解公式，称为亥姆霍兹速度分解定理。

表3.1.1 流体微团速度分解公式的物理意义和符号

若在整个流场中，流体运动若以空间坐标分类，流体运动可分为一维、二维和三维流动。为了说明式(3.1.6)中各项符号的含义，将流体空间流动的复杂情况加以分解。为了讨论的方便，首先分析图3.1.2是平面流动，即二维流动的情况，将式(3.1.6)简化为平面流动速度分解公式

图3.1.2 流体微团的平面运动

此式包含了表3.1.1中的各种不同的符号，不影响对问题的分析。流体微团的运动可以分解为下面几种形式。

(1)平移运动u

式(3.1.7)右端的第一项u_x，u_y，说明流体微团中的任一点C点有随流体微团质量中心A一起作平移运动的成分。如果θ_xx＝θ_yy＝ε_xy＝ε_yx＝ω_z＝0，则如图3.1.3(a)所示，经过dt时间后，ABCD平移到A′B′C′D′位置，微团形状不变。u_x，u_y称为微团的平移速度。

(2)直线和剪切变形运动

由于流体的易流动性，运动流体流动，流体微团发生直线变形，流体微团线性伸长或缩短，用下式表示

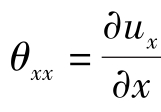的物理意义是u_x沿x方向的变化率，θ_xxdx是C、A两点（也代表CB、DA两条线）的x方向分速度的变化量。θ_yydy是C、A两点（也代表CD、BA两条线）的y方向分速度的变化量。不可压缩流体的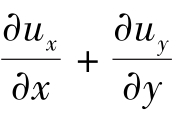＝0，如果u_x＝u_y＝ε_xy＝ε_yx＝ω_z＝0，则变成如图3.1.3(b)所示的A′B′C′D′形状。这种运动称为流体微团的直线变形运动。其中θ_xx，θ_yy，θ_zz称为直线应变速度，θ_xxdx，θ_yydy，θ_zzdz则称为流体微团的直线变形速度。

在流体运动中，流体微团发生剪切变形，即角变形。分析表3.1.1中第二列的项

式中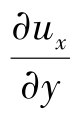，是u_x沿y方向的变化率，也叫作u_x沿y方向的速度梯度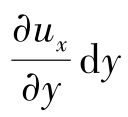，是C、A两点（也代表CD、AB两条线）的x方向分速度的变化量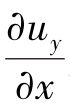；是u_y沿x方向的变化率，也叫作u_y沿x方向的速度梯度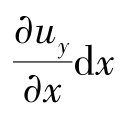；是C、A两点（也代表CB、AD两条线）的y方向分速度的变化量。由于这两个速度梯度的存在，如果u_x＝u_y＝θ_xx＝θ_yy＝0，则经过dt后，如图3.1.4所示，ABCD要变成AB″C″D″的形状，分别得到

图3.1.3 流体微团的各种运动形式

图3.1.4 流体微团的旋转与剪切变形

一般情况下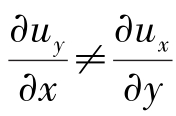，，则dθ₁≠dθ₂。假定dθ₁>dθ₂，则令(www.xing528.com)

于是

上式说明，总可用式(2)所示的另外两个角度dα与dβ的和与差来表示两个不相等的角度dθ₁和dθ₂。可以设想ABCD先整体同向旋转一个dβ角变成AB′C′D′，然后互相垂直的两边再反向各自剪切一个dα角，于是AB′C′D′最终就会变成原来由dθ₁和dθ₂所决定的AB″C″D″的形状了。

流体微团一个边的剪切角为

由式(3)得到流体微团一个边的剪切角速度为

流体微团整体的剪切角为

由式(5)得到流体微团整体的剪切角速度为

当u_x＝u_y＝θ_xx＝θ_yy＝ω_z＝0，即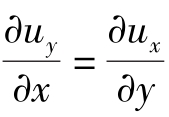，dθ₁＝dθ₂的特殊情况时，经过dt时间，ABCD发生剪切运动变成如图3.1.3(d)所示的AB′C′D′形状。使用式(1)至式(6)的推导方法，同理得到三维剪切变形（角变形）公式为

为了使用的简便，用注记符号表示法，即循环下标号表示剪切变形（角变形）为

(3)转动运动

流体微团像刚体转动一个角度。从式(1)可解出，流体微团整体的旋转角为

由式(7)可得流体微团整体的旋转角速度为

ω_z的物理意义是流体微团整体绕通过A点之z轴的转动角速度，ε_xy的物理意义是流体微团一个边绕通过A点之z轴的剪切变形角速度。式(3.1.6)第一式中的ω_zdy和ε_xydy两项自然是代表由于这两个角速度而引起的C点之x轴方向上的线速度。同样第二式中的ω_zdx和ε_yxdx则是这两个角速度所引起的C点在y方向上的线速度。由此可见，当u_x＝u_y＝θ_xx＝θ_yy＝ε_xy＝ε_yx＝0时，经过dt时间，ABCD发生旋转运动变成如图3.1.3(c)所示的AB′C′D′形状。

用流体平面运动的推导方法，得到流体空间运动的表3.1.1所示的ω_x和ω_y，得到旋度矢量ω为

用注记符号表达上式，有

将流体变形运动的符号的物理意义也列在表3.1.1中。表3.1.1中代表变形运动的符号称为流体微团的变形速度，它的9个元素组成一个沿主对角线成对称的变形速度张量S，也称为应变速度矩阵，直角坐标系的表达式为

用注记符号表达变形速度张量S_ij＝S，有

通过上面详细分解式(3.1.6)的含义，得到亥姆霍兹(Helmholtz)速度分解定理。

亥姆霍兹速度分解定理 一般情况下流体微团运动可以分解为平动、直线与剪切变形、转动三种运动之和。

亥姆霍兹的重要贡献是找到了这三种运动的数学表达式，为确定应力与变形速度的关系奠定了数学分析的基础。比较式(3.1.4)和式(3.1.6)可知，刚体和流体微团运动的主要区别在于流体微团运动多了变形速度的部分。还要注意的是，刚体速度分解定理对整个刚体而言是成立的，流体速度分解定理只在流体微团内成立，它是局部性的定理。

例题3.1.1 速度梯度张量L一般为非对称张量，请将L分解成直角坐标系的一个对称张量S与一个反对称张量ω，并说明对称张量S与反对称张量ω的物理意义。

解：按照第二章介绍张量的性质，一个二阶张量可以分解成一个对称张量与一个反对称张量之和。将速度梯度张量式(3.1.5b)恒等变形，有

将上式写成注记符号表达式

分析式(3.1.11)可见，等式右边第一个式子是一个二阶对称张量，与式(3.1.10)相同，物理意义是变形速度张量S，表征了材料变形的速率；右边第二式子就是反对称张量，与式(3.1.9)相同，物理意义是旋转速率张量ω，与材料的变形无关。

例题3.1.2 任一张量可分解为对称张量与反对称张量之和，证明该分解是唯一的。

证明：假设速度梯度张量为L＝S+ω，令

用注记符号表达上式，分别有

可见该分解是唯一的。

在场论的学习中，已经了解了流体运动以运动形式为标准分类时，若在整个流场中rotu＝Δ×u＝0，则此流动为无旋流动，反之为有旋流动。于是流体运动可分无旋流动和有旋流动两种。因为绝大多数流体运动都具有平动和变形，因此对于这两种运动形式不加分类。

变形速度张量S具有二阶对称张量的性质。

①变形速度张量S恒有三个互相垂直的主轴，以这三个主轴为正交直角坐标系，变形速度张量S可写成下列标准形式

由此可见，变形速度张量S完全由三个主相对拉伸速度决定，也就是说流体微团在主轴上的线元以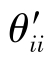的相对拉伸速度变形，变形后仍在主轴方向。

式中：I_S，II_S，III_S分别为变形速度张量的第一、第二和第三不变量。

例题3.1.3^[2]现考察I_S的物理意义。

解：根据场论散度的定义

通过封闭曲面S的速度通量∯u·dS等于体积∂V的变化率，于是

取直角坐标系的单位体积元∂x，∂y，∂z，∂V＝∂x∂y∂z，将其代入到上式中，有

由此可见，不变量I_S等于速度场的散度divu，其物理意义是流体的相对体积膨胀率。当I_S>0流体体积膨胀；I_S＝0流体无体积变化，I_S<0流体体积收缩。

可用速度散度的公式来判断流体压缩性质。当divu＝0，流体的相对体积膨胀率为零，即该流体为不可压缩流体。当divu≠0，流体的相对体积膨胀率不为零，即该流体为可压缩流体。divu＝Δ·u＝0是不可压缩流体的一种数学表示。