三个重要通量的物理意义和具体表达式在流体力学中的简述

本章的部分练习题出自参考文献[7]和[8]。

2.1 基本概念题

(1)将流体看作连续介质的条件是什么？

(2)描述流体运动的拉格朗日法(Lagrange)和欧拉法(Euler)这两种研究方法的区别，给出这两种方法的数学表达式。试写出不可缩流体在拉格朗日和欧拉观点下的数学表达式。

2.2 若A＝x²sinyi+z²cosyj－xy²k，求dA。

2.3 当Φ＝x²yz³和A＝xzi－y²j+2x²yk，请完成下列运算：

(1)ΔΦ

(2)Δ·A

(3)Δ×A

(4) div(ΦA)

(5) rot(ΦA)

2.4 (1)证明矢径r的模为数量；

(2)证明张量与矢量的点积为矢量，即证明T·a为矢量。

2.5 运用二阶张量的变换式，写出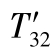的变换式。

2.6 通过证明等式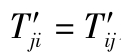来证明对称张量在坐标系转动时保持其对称性不变。

2.7 写出矢量对张量点乘的结合律和张量对矢量点乘的结合律的表达式。

2.8 已知T，R为张量，I为单位张量，A，B为矢量，u为数量，证明以下等式。

(1)TA为矢量

(2)T·R为张量

(3)A·I＝I·A＝A

(4)A·T＝T_c·A

(5)A·T＝T·A的充要条件是T为对称张量

(6) (uT)·R＝T·(uR)＝u(T·R)

2.9 已知T为张量，I为单位张量，A，B为矢量，u为数量，证明以下等式。

(1)B·ΔA＝(B·Δ)A

(2)Δ·T为矢量(www.xing528.com)

(3)Δ·(uI)＝Δu

(4)Δ·(AB)＝(Δ·A)B+(A·Δ)B

(5)Δ·(uT)＝uΔ·T+Δu·T

2.10 在球坐标系中和在柱坐标系中，分别求体积元素dV和面积元素dS，并作图。

2.11 线积分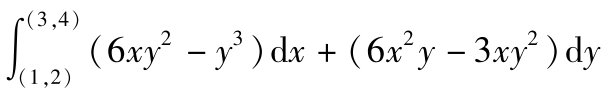与连接点(1,2)和(3,4)的路径无关，计算此积分。

2.12 计算A＝xz²i+(x²y－z³)j+(2xy+y²z)k，其中S是由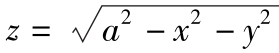和z＝0所围成半球区域整个边界的通量。

(1)应用散度定理；

(2)直接计算。

2.13 计算矢量场A＝xyz(i+j+k)在点M (1，2，3)处的旋度和在这点沿n＝i+2j+2k的环量面密度。

2.14 已知流速u＝(x+t)i+(y+t)j。令t＝0时的坐标值为a，b，求用拉格朗日法表示的速度分布。

2.15 已知以下不可压缩流场的速度分量，其中C是常数。判断流体的流动是有旋流动还是无旋流动，求出流线方程和画出流线的形状。

(1)u_x＝Cy，u_y＝u_z＝0

(2)u_x＝C，u_y＝u_z＝0

(3)u_x＝－Cy，u_y＝Cx，u_z＝0

(4)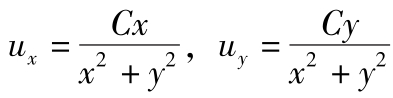，u_z＝0

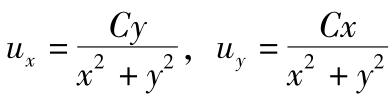(5)，u_z＝0

(6)

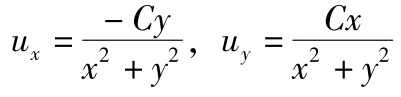
(7)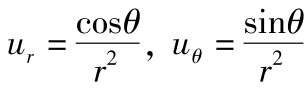，u_z＝0

2.16 概念题

(1)简述分子传递线性现象的三个重要定律，给出数学表达式。

(2)简述流体力学中三个重要通量的物理意义和具体表达式。

2.17 简述数量场的定义，写出相应的数学表达式。

2.18 简述矢量场的定义，写出相应的数学表达式。

2.19 简述张量场的定义，写出相应的数学表达式。