数量场中的方向导数和梯度：描述均衡分布情况的等值面与等值线

如果在全部空间或部分空间里的每一点，都对应着某个物理量的一个确定的数量值，就说在这个空间里确定了该物理量的一个数量场或标量场。

本小节介绍数量场的几何描述、数学表达和基本运算，包括数量场的域和等值面、数量场的梯度和哈密顿算子两部分。

这里介绍数量场的单连域、复连域和等值面等数学描述。

(1)单连域和复连域

空间域为场，在介绍数量场之前先介绍在三维空间里单连域与复连域的概念。

① 如果在一个空间区域Ω内，任何一条简单闭曲线l，都可以作出一个以Σ为边界且全部位于区域Ω内的曲面S，则称此区域Ω为线单连域；否则，称为线复连域。例如图2.4.1(a)空心球体是线单连域，而图2.4.1 (b)环面体则为线复连域。

② 如果在一个空间区域Ω内，任一简单闭曲面S所包围的全部点，都在区域Ω内（即S内没有洞），则称此区域Ω为面单连域；否则，称为面复连域。例如图2.4.1(b)环面体是面单连域，而图2.3.1(a)空心球体是面复连域。

图2.4.1 单连域与复连域

(a)空心球体(b)环面体

显然，有许多空间区域既是线单连域，同时又是面单连域，例如实心球体、椭球体、圆柱体和平行六面体等。

一个稳定数量场u是场中点M的函数u＝u(M)，当确定了直角坐标系Oxyz后，它是点M(x，y，z)的坐标函数，一个稳定数量场表示为

式中，假定数量函数u＝u(x，y，z)是一个单值、连续函数，且有一阶连续偏导数。

在工程实际中，常用到的数量场有密度场ρ(x，y，z)、温度场T(x，y，z，t)，前者表示某空间中某物质的密度不均匀，后者表示该空间里温度不一致，并且随时间变化。

(2)数量场的等值面

为了直观地研究数量u在场中的分布状况，引入了等值面、等值线的概念。由隐函数存在定理可知，当函数u＝u(x，y，z)为单值，且各连续偏导数不全为零时，这种等值面或等值线一定存在。等值面是由场中使函数u取相同数值的点所组成的曲面，其方程为

在平面数量场u(x，y)中，具有相同数值的点组成该数量场的等值线

式中，C为常数。C取不同的数值，可得到不同的等值面或等值线。

等值面或等值线充满了数量场所在的空间，而且互不相交。数量场中的每一点都有一等值面或等值线通过。数量场的等值面或等值线用图直观地表示物理量在场中的分布状况。例如聚合物加工成型的温度场中，由温度相同的点所组成的等温面。在平面问题中，例如地形图上等高线、等温线，可以了解到该地区温度的分布情况，还可根据等温线的稀密程度来大致判定该地区在各个方向上温度变化的趋势，较密的地方温度变化较大。

这里介绍数量场的数学物理意义和哈密顿算子，以及梯度的基本运算公式。

(1)数量场的方向导数和梯度

数量场的等值面或等值线描述了场中数量的整体分布情况，不能对其作局部分析。一个函数的变化率可以用该函数的导数表示。为了考察数量场u在场中各个点处的邻域内沿每一方向的变化情况，引入方向导数的概念。数量场u的方向导数表示u沿某个方向的变化率。

定义：设M₀为数量场u＝u(M)中的一点，从点M₀出发引一条射线l，在l上的点M₀的邻近取一动点M，Δl为M₀和M的距离。若当M→M₀时，下列极限

存在，则称它为数量场u(M)在点M₀处沿这个l方向的方向导数。

由定义可知，当Δl→0时，方向导数是在一个点M处沿方向l的函数u(M)对距离的变化率。当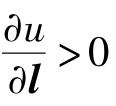时，函数u沿l方向就是增加的；当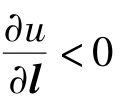时，函数u沿l方向是减少的。在直角坐标系中，数量场u(x，y，z)的方向导数由以下定理给出计算公式。

定理：在直角坐标系中，若函数u＝u(x，y，z)在点M₀(x₀，y₀，z₀)处可微，cosα，cosβ和cosγ为l方向的方向余弦，则函数u在点M₀处沿l方向的方向导数必存在，由下面的公式给出

式中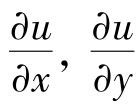，和是在点M₀处的偏导数。

推论：若在有向曲线C上取定点M₀作为计算弧长s的起点，取C之正向为s增大的方向，点M为C上一点，在M处沿C正向作与C相切的射线，如图2.4.2所示，则在点M处u可微，曲线C光滑，则有

图2.4.2 沿C正向作与C相切的射线

这就是说，函数u在点M处沿曲线C(正向）的方向导数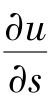与函数u在点M处沿切线方向（指向C的正向一侧）的方向导数相等。

详细证明可参看相关文献^[3]。在数量场定义的区域内，从一个给定点出发，有无穷多个方向。显然，沿各个方向的变化率可能不同。函数u(M)沿其中哪个方向的变化率最大，最大变化率是多少？需要引入梯度的概念。方向导数式(2.4.4)中cosα，cosβ和cosγ为l方向的方向余弦，即l方向的单位矢量l⁰＝cosαi+cosβj+cosγk，令(www.xing528.com)

可将方向导数写成G与单位矢量l⁰的数量积，得

式中，cos(G，l⁰)为矢量G与l⁰夹角的余弦。

由数量积的定义和式(2.4.6)可知，当l⁰方向与G方向一致时，cos(G，l⁰)＝1，方向导数取得最大值，其值为，G的方向就是u(M)变化率最大的方向，其模是这个最大变化率的数值。称G为函数u(M)在给定点处的梯度。一般有如下定义。

梯度的定义：若在数量场u(M)中的一点M处，存在这样的矢量G，其方向是函数u(M)在点M处变化率最大的方向，其模是这个最大变化率的数值，则称矢量G为u(M)在点M处梯度，记作gradu＝G。

可见，梯度的定义与坐标系的选择无关，它仅由数量函数u(M)的分布决定。在直角坐标系中，可表示为

因此，只要求出u(M)在三个正交方向的变化率，就完全确定了梯度。

梯度grad u本身又是一个矢量场，有两个重要的性质。

① 任意方向导数等于梯度在该方向上的投影，写作＝grad_lu。

② 数量场中每一点M处的梯度，垂直于过该点的等值面，且指向函数u(M)增大的一方。由式(2.4.7)可知，在直角坐标系中点M处gradu的坐标正好是过M点的等值面u(x，y，z)＝C的法线方向数，也就是说梯度是等值面的法矢量，即它垂直于等值面。

梯度是数量场中一个重要概念，在科学技术问题中广泛的应用。若把数量场中每一点梯度与场中的每一点对应起来得到一个矢量场，称为由此数量场产生的梯度场。

(2)哈密顿算子和梯度运算公式

为了书写和运算的方便，哈密顿(Hamilton)引入了劈形算符Δ，称为哈密顿算子。在直角坐标系中，哈密顿算子为

式中，Δ为微分运算符号的矢量，是矢量微分算子。在运算中，它具有矢量和微分的双重性质。

梯度的基本运算公式：

若设C为常数，u，v为数量函数，用梯度定义和函数运算规则可证明以下运算公式^[4]。

① ΔCu＝CΔu

② Δ(u±v)＝Δu±Δv

③ Δ(uv)＝uΔv+vΔu

④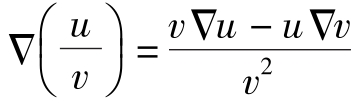

⑤ Δf(u)＝f′(u)Δu

⑥

若u为数量函数，A为矢量函数，有以下运算规则

① gradu＝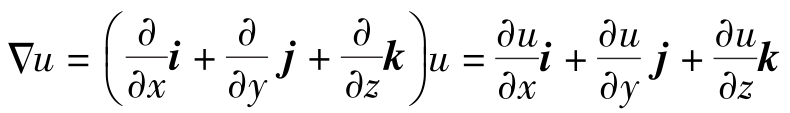

②

③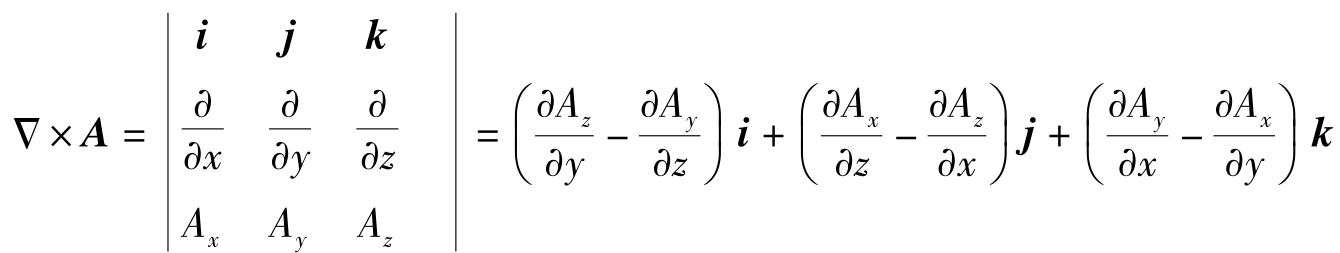

例题2.4.1^[7] 求函数u＝xy²+yz³在点M(2，－1，1)处的梯度和在矢量l＝2i+2j－k方向的方向导数。

解：应用式(2.4.7)，有gradu|_M＝[y²i+(2xy+z³)j+3yz²k]_M＝i－3j－3k

l方向的单位矢量为

得到方向导数为