传递过程中的定律和通量

传递现象是自然界和工程技术中普遍存在的现象。传递过程特指物理量朝平衡转移的过程。在传递过程中，传递的物理量有动量、能量、质量和电量等。平衡状态是指物系内具有强度性质的物理量不存在梯度，例如平衡状态的流体温度、组分浓度是相等的。对于任何处于不平衡状态的物系，一定会有某些物理量由高强度区向低强度区转移。例如，热物体向冷物体传递热量，最后两物体温度趋于一致达到温度平衡。动量、热量与质量的传递既可以由分子的微观运动引起，也可由旋涡混合造成的流体微团的宏观运动引起。前者称为分子传递，后者称为涡流传递。

由于分子的不规则运动，在各层流体间将交换着动量、质量和能量，使不同流体层内的平均物理量均匀化，这种性质称为分子运动的传递性质。动量传递在宏观上表现为黏性现象，能量传递则表现为热传导现象，质量传递表现为扩散现象。流体的宏观性质，如黏性、热传导、扩散等是分子输运性质的统计平均。

本小节介绍描述动量传递、能量传递和质量传递三种现象的定律和通量^{[5，6，8，9]}，包括三个重要的定律、传递的通量两部分。

(1)牛顿黏性定律

对于任何处于不平衡状态的流体物系，一定会有某些物理量由高强度区向低强度区转移。用牛顿黏性定律(Newton’s Viscosity Law)描述由分子运动引起的动量传递。

动量传递 ( Momentum Transfer)——在垂直于实际流体流动方向上，动量由高速度区向低速度区转移。

动量传递在宏观上表现为黏性现象。1687年，牛顿第一个做了一个著名的流体平面剪切运动的实验，建立了切向应力和剪切变形之间的关系。如图2.3.2所示，在无限大的两平行平板之间进行流体运动的实验。两块相互平行两板之间距离大大小于板的长度和宽度。两板之间有静止的流体，当下板静止，上板以不大的恒速U₀向右运动。由于流体的黏性，紧黏在板上的一层流体随平板一起运动，获得沿x方向的动量，并将其动量传递给与之邻近的流体层，两板间的流体作层流流动，建立了速度分布。由于动量传递而使两流体层之间产生剪应力。该流体的剪切流动是平面问题，由图2.3.2可见，流体微片面上的一对大小相等、方向相反的剪切应力τ_xy和τ_yx。

实验证明，剪应力与黏度和相对速度成正比，动量通量的方向与速度梯度的方向相反，得到牛顿黏性公式为

式中，在小片上下表面τ_yx为剪切应力，它们是一对大小相等方向相反的力，N/m²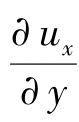；为速度梯度或剪切速率；μ为动力黏度系数（黏度系数），kg/(m·s)；“ ±”号表示动量朝着速度降低的方向传递。

图2.3.2 黏性与动量传递

张也影^[5]强调指出，牛顿摩擦定律的剪切应力的“±”号是为了保持剪切应力的正值。当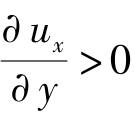时，式中取“+”号；当时，式中取“－”号，以保持剪切应力的正值。

黏度系数是流体的一种物理常数，是流体抵抗变形的内摩擦的度量。黏度系数μ依赖于流体的性质，它是流体组成、压力和温度的状态函数，与速度梯度无关。对于黏性很小的流体，μ的值很小。对于黏性很大的流体，μ的值很大，可以是水黏性系数的几千倍。实际气体和液体的黏度一般随压力的升高而增加，理想气体的黏度与压力无关。黏度系数μ显著地依赖于温度，液体的黏度随温度的升高而降低，气体的黏度随温度升高反而上升。对于气体，黏度系数μ和温度的关系用索士兰特(Sutherland)公式表示^[6]，为

式中，C≈110.4 K。

该式在相当大的范围(T<2000K)对空气是适用的。由于其复杂性，在实际中常采用幂次的公式^[6]

来表达近似真实的黏性关系，其中幂次的范围为1/2≤n≤1。在T>3000K的高温时，n≈1/2；在低温时可取为1。在90K<T<300K的温度范围，n≈8~9，它与索士兰特公式的计算误差不超过5%。可从工程手册查到大多数流体的黏度系数，也可用专门的黏度仪器实验测量。第7章将介绍流变测量仪的基本原理和应用。

牛顿流体是遵循牛顿黏性定律的流体，包括气体、水和低相对分子质量的大多数液体。

非牛顿流体是不遵循牛顿黏性定律的流体，包括泥浆、污水、聚合物溶液、油漆等。流变学(Rheology)主要研究非牛顿型流体。本书重点讨论非牛顿型聚合物流体。

(2)傅立叶定律

能量传递表现为热传导现象。用傅立叶定律(Fourie’s Law)描述由分子运动引起的热量传递，即描述导热现象。

能量传递(Energy transfer)——热量由高温度区向低温度区的转移。热物体向冷物体传递热量，最后两物体温度趋于一致达到温度平衡。

傅立叶定律：“在场中任一点处，沿任一方向的热流强度（即在该点处单位时间内垂直流过单位面积的热量）与该方向上的温度变化率成正比”。在场中之任一点处，沿n方向的热流强度记为

式中，q为单位面积的热流通量（热流矢量或热流密度），J/(m²·s)；κ为物质导热系数，κ>0，W/(m·K)；dT/dn＝ΔT为温度梯度，K/m；式中负号表示热通量方向与温度梯度方向相反，即热量朝着温度降低的方向传递。

导热系数κ是物质的物理性质。对于同一物质，导热系数主要是温度的函数，压力对它的影响不大。在高压或真空下，气体的导热系数受压力的影响。在一般情况下，讨论各向同性导热，导热系数与方向无关。

(3)费克定律

质量传递表现为扩散现象。在混合物中，若各组分存在浓度梯度时，发生分子扩散，浓度高的地方向浓度低的地方输送该组元的物质。分子质量扩散传递同分子的动量扩散传递一样，是分子无规则运动的结果。用费克定律(Fick’s Law)描述分子运动引起的质量传递。

质量传递(Mass transfer)——流体物系中一个或几个组分由高浓度区向低浓度区的转移。

1855年，费克首先提出了质量分子扩散的基本关系式——费克定律:“对于两组分系统，在单位时间内组分A通过与扩散分子扩散y方向相垂直方向上单位面积的质量与该方向上的浓度变化率成正比”。所产生的质量通量表示为(www.xing528.com)

式中，j_A为组分A的扩散质量通量，kg/(m²·s)；D_AB为组分A在组分B中的扩散系数，与组分的种类、组成和温度有关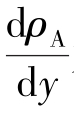；为组分A的质量浓度（密度）梯度；式中负号表示质量通量的方向与浓度梯度方向相反，即组分A总是朝着浓度降低的方向传递。扩散系数D_AB与组分的种类、温度和组成等因素有关。

动量、热量与质量的传递之所以发生，是由于物系内部存在着速度梯度、温度梯度和浓度梯度的缘故。动量、热量与质量传递是一种探讨速率的科学，三者之间具有许多类似之处，它们不但可以用类似的数学模型来描述，而且描述三者的一些物理量之间还存在着某些定量关系。这些类似关系和变量关系使研究三种传递过程的问题得以简化。比较牛顿黏性、傅立叶传热和费克传质这三个著名定律的数学表达式，不难发现动量、热量与质量输运传递过程的规律有类似性。

各传递过程中的物理量都与其相应的强度因素成正比，并且都沿着负梯度的方向传递。各式中的输运系数只是状态的函数，输运传递的物理量与相应的梯度之间存在着线性关系。有必要分别介绍动量通量、热量通量与质量通量的普遍表达式。

(1)动量通量

假设被研究的流体为不可压缩流体，其密度ρ为常数，在x方向上作一维流动，将牛顿黏性定律式改写为

其中，

式中，ν为运动黏度或动量扩散系数，m²/s；τ为剪应力或动量通量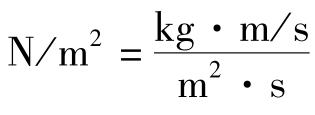，；ρu_x为动量浓度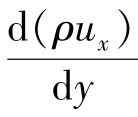，；为动量浓度梯度，。

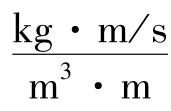(y方向上的动量通量)＝－(动量扩散系数)×(y方向上的动量浓度梯度)

(2)热量通量

对于物系常数k，c_p，ρ均为恒值的导热问题，将傅立叶定律式改写为

其中，

式中，q为热量通量，J/(m²·s)；α为导热系数，可称为热量扩散系数，m²/s；ρc_pt为热量浓度，J/m³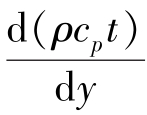；为热量浓度梯度，J/(m³·m)。

由式(2.3.20)和各量的单位可以看出，傅立叶定律说明了热量通量q[J/(m²·s)]等于热量扩散系数α(m²/s)与热量浓度梯度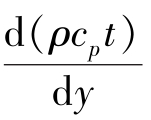_[J/(m³·m)]乘积的负值。该式的物理意义用文字方程可表示为

(温度梯度引起y方向上的热量通量)＝－(热量扩散系数)×(y方向上的热量浓度梯度)

(3)质量通量

流体物系中一个或几个组分由高浓度区向低浓度区的转移。直接分析费克定律表达式(2.3.17)和各量的物理意义，有

式中，j_A为组分A的质量通量，kg/(m²·s)；D_AB为组分A的质量扩散系数，m²/s；ρ_A为组分A的密度或质量浓度，kg/m³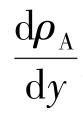；为质量浓度梯度，kg/(m³·m)。

由式(2.3.17)和各量的单位可看出，费克定律说明了组分A的质量通量j_A[kg/(m²·s)]等于质量扩散系数D_AB(m²/s)与质量浓度梯度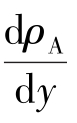[kg/(m³·m)]乘积的负值。该式的物理意义用文字方程可表示为

(浓度梯度引起组分A在y方向上的质量通量)＝－(质量扩散系数)×(y方向上组分A的质量浓度梯度)

通过对三种传递现象的分析，可得到如下结论:

① 由于动量、热量和质量传递的通量，均等于各自的扩散系数与各自量浓度梯度乘积的负值。3种分子传递过程可以用一个普遍表达式现象方程表示为

(通量)＝－(扩散系数)×(浓度梯度)

现象方程中的“负号”表示传递方向与坐标轴方向相同，而梯度与坐标轴方向相反。

② 动量、热量和质量扩散系数ν，α，D_AB具有相同的因次，其单位均为m²/s，可分别用式(2.3.19)、式(2.3.21)和式(2.2.17)的定义。可见，三者的定义式均为微分方程。而动量、热量和质量浓度梯度分别表示该量传递的推动力。

③ 通量为单位时间内通过与传递方向相垂直的单位面积上的动量、热量和质量，各量的传递方向均与该量的浓度梯度方向相反。