描述流体运动的基本知识

本小节介绍描述流体运动的基本概念，包括连续介质的假设、流体的性质及其分类、描述流体运动的两种方法3部分。

实际流体由大量有空隙并进行复杂微观运动的大量分子组成，每个分子作无休止不规则的运动，分子之间交换动量和能量。在时间和空间上，流体的微观结构和运动是不均匀、离散和随机的。用仪器测量观测到流体的宏观结构以及流体运动具有均匀性、连续性和确定性。因此研究流体的宏观机械运动时，流体力学一般采用连续介质的假设，当流体系统的特征长度远远大于流体分子运动自由程，即≫，流体流动的系统可看成是连续系统。

连续介质假设是流体力学中第一个根本性的假设。认为流体微团连续地充满流体所在的整个空间。所谓的流体微团指的是微观上充分大，宏观上充分小的分子团。也就是说，一方面在微观上流体微团的尺度足够大，大到包含大量的分子，使得统计平均后能得到其物理量的确定值；另一方面在宏观上流体微团的尺度又足够的小，远小于所研究问题的特征尺度，使得其平均物理量可看成是均匀不变的，因而可将它近似看成几何上没有维度的一个质点。

当流体力学引进了连续介质假设，大量离散分子运动将近似为连续充满整个空间流体微团的运动问题，不再考虑流体的分子结构，流体被看成是宏观均匀连续体，而不是微观的包含大量分子的离散体。流体质点的位移，不是指个别分子的位移。而是指包含大量分子的流体微团的位移。这样就可以把流体的物理量作为空间和时间的连续函数，利用数学分析工具研究流体流动的问题。即流体微团所具有的质量、速度、压力和温度等宏观物理量满足一切应该遵循的物理定律和性质，例如牛顿定律、质量、能量守恒定律、热力学定律，以及扩散、黏性、热传导等输运性质。

描述流体运动状态的物理量主要是速度，与流体运动密切相关的流体特性有压强、密度、浓度、温度和能量，可统称为流动的基本特性参数。由前一节可知，其中速度和压力是矢量，密度、浓度、温度和能量是数量。

这里简要介绍流体的易流动性、黏性和压缩性等宏观性质，并介绍基于流体性质的流体分类^[6]。

(1)易流动性

流体是液体和气体的总称，是由大量的不断地作热运动而且无固定平衡位置的分子构成的，它的基本特征是没有一定的形状和具有流动性。流体与固体不同，静止的流体不能承受切向应力，只要连续施加不管多小的切向应力，都能使流体流动发生任意大的变形。这是流体区别于固体的主要特性。在静止时，流体只有法向应力而没有切向应力，而静止的固体可以承受切向应力。液体的这个宏观性质称为易流动性。固体中分子间的作用力较强，有固定的平衡位置，因而固体不但具有一定的体积，而且具有一定的形状。固体承受外界力作用时，它可作微小的变形，然后承受住剪切应力不再变形。与其相反，流体和气体中分子间的作用力较弱或很弱，很小的剪切应力都可能使其产生任意大的变形发生流动。

需要注意到，有些物质的性质介于固体和流体之间，例如胶状物、沥青等一类触变物质在不同的条件下有不同的特性，浓缩的聚合物同时存在着类似固体和流体的性质，第4章和第5章将分别详细介绍聚合物流体的流动特性和流变模型。

(2)理想流体和黏性流体

黏度为零的流体称为理想流体，有时也称为“完全流体”。实际上自然界并不存在理想流体，真实流体运动时都会表现出黏性。黏性是流体的固有属性。但是，考虑流体的黏性，将使流体运动的分析变得非常复杂。在流体力学中，为了简化理论分析，通常引入不考虑黏性的“理想流体模型”。引入理想流体的概念，对研究实际流体起着很重要的作用。理想流体运动的基本方程是欧拉方程。在运动时，流体相邻两层流体之间存在相对运动，流体抵抗相对滑动的速度，这种抵抗力称为黏性应力。流体所具有的这种抵抗两层流体相对滑动速度，或普遍来说抵抗变形的性质称为黏度。黏度大小依赖于流体的性质，且显著地随温度而改变。除了黏性外，流体还有热传导和扩散等性质。可以说，理想流体是不考虑黏性、热传导、质量扩散等扩散特性的流体。

(3)不可压缩流体和可压缩流体

当运动流体微团的质量一定时，由于压力、温度等因素的改变，流体微团的体积或密度多少有所改变。在一定压力差或温度差的条件下，运动流体微团的体积或密度可以改变的性质称为压缩性。按照流体的压缩性将流体分成不可压缩流体和可压缩流体两大类。

实际流体都是可以压缩的，其压缩程度依赖于流体的性质和外界条件。在通常压力或温度条件下，液体的压缩性很小。在液体中分子之间存在着一定的作用力，它使分子不分散远离，保持一定的体积，因此要使液体改变体积是较难的。在通常的压力和温度下，液体压缩性很小，例如水在100个大气压下，体积缩小0.5%，温度从20℃升高到100℃，体积降低4%。因此在一般情况下，通常液体可近似看成不可压缩的流体。对于某些压力非常大的特殊情况，如水中爆炸或水击等问题，水是可压缩的流体。

对气体而言，分子间作用十分小，它不能保持固定的形状及大小。因此，在同样外界条件作用下，气体可较大改变其体积。但是，对低速运动而温度差又不大的气体也可近似视为不可压缩的流体，而高速运动的气体是可压缩流体。由此可见，实际流体都具有压缩性，不可压缩流体是在某种条件下实际流体的近似模型。

描述流体的运动要表示空间点的位置、速度和加速度，已经建立了描述流体运动的拉格朗日法和欧拉法两种基本研究方法^[6,7]。本小节介绍这两种方法，包括拉格朗日法、欧拉法、欧拉变数和拉格朗日变数的相互转换3部分。

(1)拉格朗日法 (Lagrange)

这种方法是质点力学系研究方法的自然延续。着眼点是流体质点，以流场中个别质点的运动作为研究的出发点，从而进一步研究整个流体的运动。通过两个方面来描述整个流动的情况：

① 某一运动的流体质点的密度、速度等各种物理量随时间的变化；

② 相邻质点间这些物理量的变化。

由于流体质点是连续分布的，在每一时刻每一质点都占有唯一确定的空间位置，点的矢径r＝f(M，t)＝r(M，t)是点的标志和时间的函数，在t＝t₀时刻，流体质点所在坐标系的位置a，b，c作为质点的标志。任意流体质点(a，b，c)在空间运动时，各质点在任意时刻的空间位置，将是a，b，c和时间t的函数，在直角坐标系中位置表示为

式中，a，b，c，t称为拉格朗日变数。

在r＝r(a，b，c，t)中，不同的质点将有不同的(a，b，c)值：

① 当a，b，c固定时，t变化，此式表示某一流体质点的运动轨迹；

② 当t不变，a，b，c变化，表示t时刻不同流体质点的位置分布函数。

式(2.3.1)可以描述所有质点的运动。因为矢径函数r不是空间坐标的函数，而是质点标志的函数。不同的a，b，c代表不同的质点。若用矢径r＝xi+yj+zk表示质点位置，各质点在任意时刻的空间位置r＝r(a，b，c，t)，将是a，b，c，t这4个量的函数。显然，在t＝t₀时刻，各质点的坐标值等于a，b，c，即

同理，其他物理量也表示为拉格朗日变数a，b，c，t的函数。在直角坐标系中，用拉格朗日法表示流体的速度、加速度分别为

即

流体的密度、压力、温度也可表示为拉格朗日变数a，b，c，t的函数

ρ＝ρ(a，b，c，t)

p＝p(a，b，c，t)

T＝T(a，b，c，t)

举一个例子说明拉格朗日法和拉格朗日变数在工程中的应用。

例题2.3.1^[7]已知用拉格朗日变数表示流体的速度为

式中，a，b是t＝0时刻流体质点的直角坐标值。试求：

① t＝2时刻流场中质点的分布规律；

② a＝1，b＝2这个质点的运动规律；

③ 确定流体运动的加速度。

解：将已知速度代入式(2.3.4)，得

积分上式，得

将初始条件，t＝0时刻x＝a，y＝b代入式(2)，得

求解上式确定积分常数C₁＝－1和C₂＝－1，将积分常数再代入式(2)，得各流体质点的一般分布规律

① t＝2时刻，流场中质点的分布规律，由式(3)得

② 确定a＝1，b＝2质点的运动规律，由式(3)得

③ 确定流体加速度，使用式(2.3.5)对式(3)求二阶导数，或对速度式(1)求导得

在任意曲线坐标中可以使用拉格朗日(Lagrange)法。例如，在任意正交曲线坐标q₁，q₂，q₃中，流体质点的分布规律可写成

q_i＝q_i(a，b，c，t) (i＝1，2，3)

式中，a，b，c为t＝t₀时刻的q_i坐标值，可写成

(2)欧拉法(Euler)

它不着眼于研究个别质点的运动特性，而是以流体流过空间某点时的运动特性作为研究的出发点，从而研究流体在整个空间里的运动情况。欧拉法着眼点是空间的点，用场论研究物理量的变化，在空间中每一点上描绘出流体运动随时间的变化状况。欧拉法通过两个方面来描述整个流场的情况：

① 在空间固定点上流体的各种物理量随时间的变化；

② 在相邻的空间点上这些物理量的变化。

流体运动时，同一空间点在不同的时刻由不同的质点所占据。在欧拉法中，各物理量将是空间点坐标q₁，q₂，q₃和时间t的函数。例如，流体的速度、压力和密度可分别表示为

式中，用以识别空间点的坐标值q₁，q₂，q₃和时间t称为欧拉变数。

在直角坐标系中速度场可表示为(www.xing528.com)

按照欧拉法的观点，整个流动问题的研究从数学上看就是研究一些含有时间t的矢量场和数（标）量场。如用N代表流体的某个物理量，则表达式为

N＝N(q₁，q₂，q₃，t)

此式表述了两个含义:

① 当t变化，q₁，q₂，q₃固定，它代表了空间中某固定点上，某物理量函数随时间的变化规律；

② 当t固定，q₁，q₂，q₃变化，它代表某一时刻中，在空间中，某物理量函数的分布规律。

(3)欧拉变数和拉格朗日变数的相互转换

同一个物理现象用两种不同的方法描述，这两种方法一定是等价的。对于同一个流动问题，既可用拉格朗日法也可用欧拉法来描述，在数学上这两种方法可以互相转换。

① 拉格朗日变数变换为欧拉变数

若已知用拉格朗日变数表示的函数N＝N(a，b，c，t)，将a＝a(x，y，z，t)，b＝b(x，y，z，t)，c＝c(x，y，z，t)代入N＝N(a，b，c，t)中，可得到用欧拉变数表示的函数

N＝N[a(x，y，z，t)，b(x，y，z，t)，c(x，y，z，t)，t]

如速度可表示为

即u(r，t)＝u(x，y，z，t)为欧拉变数表示的速度函数。

② 欧拉变数变换为拉格朗日变数

若已知u(r，t)＝u_xi+u_yj+u_zk是由三个方程组成的确定r(t)的常微分方程组，有

积分此式，可得

式中，C₁，C₂，C₃为积分常数，它们与t＝t₀时刻的拉格朗日变数a，b，c有关，于是有

当t＝t₀， r＝r₀，反解之得， r₀＝r(C₁，C₂，C₃)，则 C₁＝C₁(r₀)，C₂＝C₂(r₀)，C₃＝C₃ ( r₀)。为确定曲线坐标C₁， C₂， C₃的方程，将C_i取为区别不同质点的曲线坐标a， b， c，这样得到r＝r( a，b，c，t)，即欧拉变数变换为拉格朗日变数。

用拉格朗日法的观点讨论质点的运动，是通过描述不同流体质点运动规律的途径来描述整个运动，流体质点的运动规律表示为r＝r(a，b，c，t)，它的几何表示是轨迹，即流体质点在不同时刻所形成的曲线为质点运动的迹线或轨迹。由物理学知识可知，质点运动迹线或轨迹方程为

式中，t为自变量，x，y，z是t的函数，对时间t积分，积分后在所得的表达式消去时间t后，即得到质点运动的迹线或轨迹。

用欧拉法描述流体运动，矢量场为流速场，矢量线就是流线。对于三维流动瞬时速度为u(r，t)＝u_xi+u_yj+u_zk，在给定的某一瞬时t，取流场流线上的点M，又在点M处沿流线取一微分线段dr，由于dr无限小，故它与点M处的切线重合，即与u方向一致。微分线段dr的表述

dr＝dxi+dyj+dzk

得流线方程为

dr×u＝0

即

从上式可得到流线方程为

用一例题说明欧拉法和拉格朗日这两种方法的转换。

例题2.3.2^[7]已知直角坐标系速度场，其欧拉法表达式为u_x＝x+t，u_y＝y+t。求：

① 一般的迹线方程，令t＝0，x＝a，y＝b；

② 在t＝1时刻，过x＝1，y＝2点的质点迹线；

③ 在t＝1时刻，x＝1，y＝2的流线，并求其方向；

④ 以拉格朗日变数表示速度分布u＝u(a，b，t)。

解：① 由迹线方程式(2.3.11)，得

注意求迹线是对时间积分。对时间积分上式，得

确定积分常数，当，解出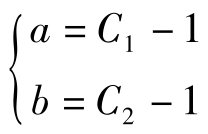，得积分常数为

将上式代入式(1)，得到随时间变化的一般迹线方程

② 在t＝1，在点(1,2)上，即质点在

求出

将上式代入式(2)，得到过点(1,2)的质点迹线为

③ 确定在t＝1，过点(1,2)的流线。由流线方程式(2.3.12)，得

(t是常数)

积分此式，得

ln(x+t)＝ln(y+t)+lnC

即

x+t＝C(y+t)

由初始条件t＝1，过点(1,2)，代入上式，定出常数C＝2/3，再代入上式，得

x+t＝2(y+t)/3

因此，在t＝1时刻，过x＝1，y＝2点的流线方程为

x+1＝2(y+1)/3

整理后，即

y＝3x/2+1/2

定出一点u_x，u_y的方向可知流线的方向。因为u_x＝x+t，u_y＝y+t，当t＝1时，u_x>0，u_y>0，t＝1时刻的流线方向，如图2.3.1所示。注意流线不是时间的函数。

图2.3.1t＝1时流线方向

④ 因为，由拉格朗日变数表示的速度为

把迹线方程(2)代入以欧拉变数表示的速度分布线，也可得到式(3)。