二阶张量的性质详解

全面描述聚合物流体内部的黏弹性应力及其变化情形，需要学习掌握应力张量的基本知识。本小节介绍二阶张量的基本知识^[4,7]，包括二阶张量的定义、二阶张量的性质两部分。

二阶张量由3个矢量来表示，由9个数的分量组成。在坐标系中，张量由其9个分量的集合确定，当坐标系转动时这9个数量按一定的规律变换，张量所表示的物理量和几何量与坐标系的选择无关。首先以并矢量的概念引入二阶张量。

例题2.2.1 已知矢量a＝a₁e₁+a₂e₂+a₃e₃和b＝b₁e₁+b₂e₂+b₃e₃。试证明矢量a_ib_j (i， j＝1，2，3)有9个分量^[4]。

证明：将坐标系Ox₁x₂x₃转动成为后，有变换式

且有

由上式可见，a_ib_j按(2.2.1)变换规律式变换，ab由三个矢量按照一定规律组成，有9个数量的分量。矢量ab的方阵式可写为

必须注意到，一般ab≠ba。由并矢量引入新的量

式中，e_ie_j是并矢量，不能写为e_je_i。该并矢量称为二阶张量。

例题2.2.2 当坐标系Ox₁x₂x₃转动为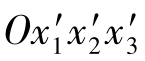，二阶张量的9个分量就要发生变化，运用坐标变换的矢量变换式，推导二阶张量T_ij和的变换关系式^[4]。

解：现将以矢量坐标变换知识加以推广。

① 首先找出朝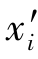轴的正方向通过新的侧面上单位面积的力与原来的力T_i之间的关系。由式(2.2.3)分别可得

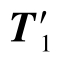② 利用矢量的变换式＝β₁₁a₁+β₁₂a₂+β₁₃a₃，把分别向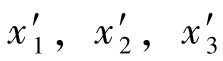轴投影，把β₁₁T₁+β₁₂T₂+β₁₃T₃分别向x₁，x₂，x₃轴投影，可得到的变换式

用同样的方法可找到其余8个分量的变换式。以上过程也可以统一推导如下。把式(2.2.4)写成统一的形式

把上式两边都看作矢量a，分别代入式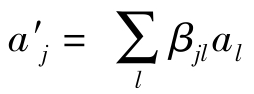的两边，得

可删除求和符号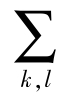，直接用循环下标表示求和，缩写为

式(2.2.5a)和式(2.2.5b)就是二阶张量的变换关系式。请读者注意式中循环下标的写法。

二阶张量的变换关系式表明，如果三维空间的某个物理量要9个数量表示，当坐标系转动后，这9个数量按照式(2.2.5)的规律变换，该物理量就是二阶张量。现在以坐标变换为基础的矢量定义加以推广，来定义张量。(www.xing528.com)

张量定义：设某量T是由9个分量T_kl构成的有序总体，如果从一个直角坐标系Ox₁x₂x₃按照式(2.2.5)变换规律变换到另一个直角坐标系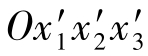中的9个分量，则该量T称为笛卡尔二阶张量，简称二阶张量。T_kl和称为笛卡尔二阶张量的分量。

推广：如果三维空间的物理量需用3ⁿ个数量表达，当正交坐标系转动后，这些数量按以下规律变换

这样的3ⁿ个数量的有序集合就是三维空间的一个n阶张量。在这种定义下，标量（数量）是零阶张量，矢量是一阶张量。

二阶张量可简称为张量，常用大写字母T，P，J等符号表示。张量的分量形式常用解析式(2.2.3)或方阵来表示。张量T方阵表示式

两个相等的张量，这两个张量的分量必须分别对应相等。

张量T由3个矢量组成，张量T的矢量表示式为

设T＝T_ij是1个二阶张量，若T_c＝T_ji也是一个二阶张量，T_c称为T的共轭张量或转置张量。张量T和T_c的表达式分别为

显然共轭是相互的，将T_c再转置，有

二阶张量T的分量满足T_ij＝T_ji的关系，该张量称为二阶对称张量。对称张量式为

由式(2.2.11)可知，二阶对称张量只有6个独立的分量，且满足T＝T_c的关系。流变学、流体力学、弹性力学中的应力张量和应变张量都是二阶对称张量，δ_ij克罗内克符号也是二阶对称张量。

请读者注意张量T方阵表示式中每一项下标的不同之处和规律。

如果张量T的分量满足T_ij＝－T_ji的关系，该张量称为二阶反对称张量或斜对称张量。反对称张量主对角线元素均为零，只有3个独立分量，且满足T＝－T_c的关系。反对称张量可表示为

单位张量I的分量为δ_ij，其表达式为

例题2.2.3 当坐标系转动时，如果一个张量的分量保持不变，那么称此张量为对这种变换的不变张量。试证明单位张量为不变张量^[4]。

证明：将坐标系Ox₁x₂x₃转动成为后，单位张量的分量δ_ij用表示，有

由上式可见，单位张量的分量保持不变，因此单位张量为不变张量。