矢量函数的基本概念

在工程实际中，经常遇到既有大小又有方向的量，例如一个物体运动的速度。数学上用矢量A表示既有大小又有方向的量。为了研究变矢量与某个数量的关系，引入矢量函数。矢量函数是随自变量变化的向量，自变量可以是一个，也可以是多个。

本小节介绍矢量函数的基本概念，包括矢量函数的定义、矢量函数的几何描述两部分。

(1)矢量函数的定义

定义：如果对于数量t在某个范围Ω内的每一个数值，变矢量A都有一个确定的矢量与它对应，则称A为自变量t的矢量函数。记作

① 全书主要物理量符号说明见附录3，无特殊情况不再注释。

并称Ω为函数A(t)的定义域。

矢量函数A(t)的直角坐标表达式为

式中，A_x(t)，A_y(t)和A_z(t)为A(t)在Oxyz坐标系中的三个坐标，i，j，k为沿三个坐标轴正向的单位矢量。

一个矢量函数和三个有序的数量函数构成一一对应的关系。本书介绍的矢量均为自由矢量。当两矢量的模和方向都相同时，就认为两矢量是相等的。

由于一个矢量函数和三个有序的数量函数构成一一对应的关系。由此可知，矢量函数的极限定义与数量函数的极限定义相类似，可将数量函数中的一些极限运算的法则用于矢量函数极限的运算。这里不作详细介绍，仅给出矢量函数连续性的定义。

矢量函数连续性的定义：若矢量函数 A ( t)在点 t₀的某个邻域内有定义，而且有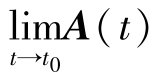＝A(t₀)，则称A(t)在t＝t₀处连续。若矢量函数A(t)在某个区间内每一点处连续，则称它在该区间内连续。矢量函数A( t)在点t₀处连续的充要条件是它的三个数量函数A_x( t)， A_y( t)和A_z( t)都在t₀处连续。

(2)矢量函数的几何描述(www.xing528.com)

矢量函数的几何描述是用图形来描述矢量函数A(t)的变化状态。把A(t)起点取在坐标原点，当t变化时，矢量A(t)的终点M就描绘出一条曲线l，如图2.1.1所示，这条曲线称为矢量函数A(t)的矢端曲线。式(2.1.2)为此曲线的矢量方程。当t变化时，矢量A(t)实际上就成为其终点M(x，y，z)的矢径。因此，A(t)的三个坐标就对应地等于其终点M的三个坐标x，y，z，即

图2.1.1 矢端曲线

式(2.1.3)是曲线l以t为参数的参数方程。

由上式可知，A(t)＝xi+yj+zk，矢量A(t)的模为

在矢量代数中，模和方向都保持不变的矢量称为常矢量。零矢量的方向为任意，可作为一个特殊的常矢量。模和方向或其中之一不断变化的矢量称为变矢量。

例题2.1.1 高等数学中给出①图2.1.2 (a)螺旋线圆柱螺旋线的参数方程为 x＝Rcosα， y＝Rsinα， z＝bα和②图2.1.2 (b)摆线的参数方程为x＝R(α－sinα)， y＝R(1－cosα)，分别确定这两条曲线的矢量方程。

解：①设有直角三角形的纸片，它的一锐角为α，将此纸片卷在一正圆柱面上，正圆柱的半径为R，使角α的一边与圆柱的底圆周重合，角α的顶点L在圆柱底圆周上的位置为A，而A为底圆周与x轴的交点，取坐标系如图2.1.2(a)所示。设角的另一边在圆柱面上盘旋上升形成的一条圆柱螺旋空间曲线。圆柱螺旋线的参数方程为x＝Rcosα，y＝Rsinα，z＝bα，则其矢量方程可写为

r＝Rcosαi+Rsinαj+bαk

② 一圆沿定直线滚动时，圆周上一定点所描述的轨迹称为摆线，如图2.1.2(b)所示。摆线的参数方程为x＝R(α－sinα)，y＝R(1－cosα)，则其矢量方程可写为

r＝R(α－sinα)i+R(1－cosα)j

图2.1.2 螺旋线和摆线