液晶超材料在THz波段的EIT和EIA效应

下面将研究双开口谐振环超材料在THz波段的传输特性。对于THz波垂直入射超材料的情况,当入射光的电场分量与谐振环开口方向夹角θ分别为0°、40°和90°时,得到了如图8.19(a)所示的透射光谱线。对于θ=0°的情况,器件的透射光谱线在0.86 THz处存在一个带宽为400 GHz的谐振谷。通过CST Microwave Studio软件模拟了谐振环的表面电流分布,如图8.19(b)所示。此时的振荡电流主要集中在谐振环的上下两部分,形成了电偶极共振模型,定义这种情况为明模式。对于θ=90°的情况,器件的透射光谱线在0.86 THz处存在一个透射峰,并且在0.4 THz和1.1 THz处分别出现谐振谷。通过模拟0.86 THz频率处的表面电流分布发现,振荡电流通过谐振环的中心线后分别流向左右两部分,最终形成两个环形回路,如图8.19(c)所示。这意味着破坏了原有的电偶极共振模式,定义为暗模式。当夹角处于中间值时,例如θ=40°时,由于同时存在两个谐振模式,相比θ=0°的透射光谱线,位于0.86 THz的谐振位置和透射率都出现了变化。由此可以看到,双开口谐振环超材料对入射光的偏振态十分敏感。

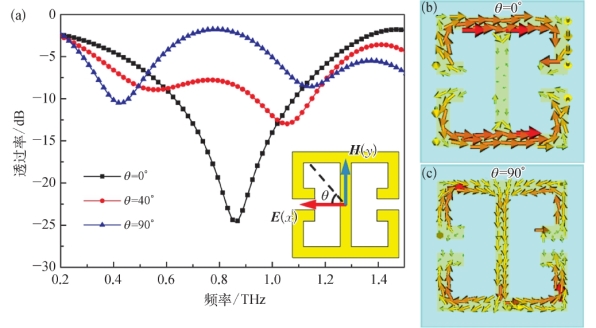
图8.19　

(a)不同入射角度的超材料透射光谱;(b)θ=0°时超材料谐振单元的表面电流分布;(c)θ=90°时超材料谐振单元的表面电流分布[18]

当施加y方向的电场时,如图8.20(a)所示,对于θ=0°的情况,器件透过率随着驱动电场的强度变化而改变。在电场强度从0变化到9 k V/m的过程中,谱线谐振位置出现红移,从0.86 THz移至0.81 THz,如图8.20(b)所示;随着电场强度继续增高至17 k V/m,谱线的谐振位置逐渐发生分裂,并分别向低频和高频移动。定义功率透射比为T=20lg(t),在上述谱线变化过程中,在0.86 THz频率处的功率透射比从初始的谐振谷-25.3 dB逐渐升高至-7.0 dB,经历了一个从谐振谷到透射峰的转变。此时该超材料器件出现了可调控电磁致诱导透明现象,中心频率在0.86 THz,带宽为260 GHz,调制深度为18.3 dB,并且谐振分裂过程和调制深度能够同时随着驱动电场的增加而增大。

图8.20　θ=0°时,液晶超材料示意图及其对应的透射光谱线[18]

(a,c)液晶超材料示意图;(b,d)透射光谱线

当外电场改为沿x轴方向且θ=0°时,如图8.20(c)所示。实验结果表明,在电场强度自0增加到17 k V/m的过程中,初始谐振位置从0.81 THz红移至0.72 THz,并伴随着谐振强度轻微降低,对应的光功率谱线如图8.20(d)所示。在此条件下,未发现电磁致诱导透明现象。

由于超材料结构的谐振对入射光的偏振态具有依赖特性,如果入射THz波的偏振态或是相位在液晶层发生改变,该器件的功率透射光谱线和谐振位置就会发生变化。对于该器件,没有施加电场时,超材料的表面结构对液晶分子存在锚定作用,因此在器件交界面处液晶分子沿着谐振环开口方向排列。然而,在毫米厚液晶盒中液晶分子的预取向排列几乎不可能具有均匀一致性,尤其在另一面硅基底没有取向层的条件下。这意味着未施加电场时,液晶分子在器件里整体呈现随机分布;当偏置电压增大时,液晶分子将趋向电场线方向排列。如果偏置电场与谐振环开口方向相互垂直,液晶分子将会形成扭曲排列,如图8.21(a)所示,此时的液晶层可以作为电控相位延迟器和偏振旋转器。然而,当偏置电压沿着谐振环开口方向时,液晶分子将会沿外电场方向逐渐形成均匀一致的排列,如图8.21(b)。在这种情况下,液晶层仅仅起到相位延迟器的作用。

图8.21　不同外电场方向的液晶超材料工作原理示意图

(a)外电场沿y轴;(b)外电场沿x轴(www.xing528.com)

因此由于液晶层的旋光效应和双折射效应,入射THz波的线偏振态能够转变为椭圆偏振态,随后与超材料相互作用,器件工作原理示意图如图8.22(a)所示。假设入射光的偏振态沿x轴方向,通过液晶层后各个电场分量如图8.22(b)所示,对应分量的表达式为

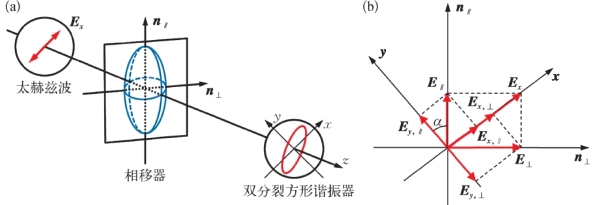
图8.22　THz波电场分量在液晶器件中偏振态的变化过程和分解示意图

(a)变化过程;(b)分解示意图

式中,E∥和E⊥表示入射光电场分量E x分别平行和垂直于长轴的分量;λ表示波长;Δδ是由液晶引起的相移;β是液晶偏振旋转器引起的偏振旋转角;P是液晶由驱动电场形成的有效螺距;Δn表示液晶材料的双折射系数。利用上述公式,可以得到光场强度I在笛卡尔坐标系中各坐标轴分量的相干耦合强度I x、I y分别为

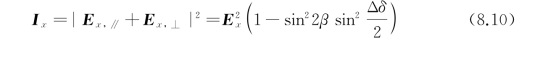
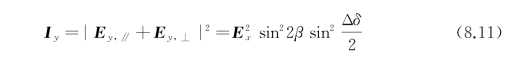
式中,E i,∥和E i,⊥(i=x,y)分别是电场分量E∥和E⊥在笛卡尔坐标系中的坐标轴分量。

根据式(8.10)和式(8.11)可知,光强度I i是偏振旋转角β和相移Δδ的函数,并且由电场驱动的液晶分子排列方向决定β和Δδ的大小,而不仅仅取决于液晶折射率的变化。光强度分量I x对应于θ=0°的明模式,分量I y对应θ=90°时的暗模式,并且通过上述两个模式的相干耦合产生了如图8.20(b)所示的电磁致诱导透明现象。

对于图8.20(a)的情况,当未施加偏置电压时,只存在I x分量与超材料相互作用,所以仅在0.86 THz处存在电偶极谐振。当施加沿y轴方向的电场后,液晶表层分子逐渐沿y轴转向且在液晶盒中形成扭曲形结构。当扭曲液晶层形成最大的螺距时,令P max=4d,d=1.2 mm,Δn=0.15并代入式(8.9),可以得到在0.86 THz处偏振旋转角β的极大值为0.26πrad。同时,由于液晶的双折射效应,相移Δδ在0.86 THz处从0逐渐增至πrad。根据式(8.10)和式(8.11)可知,越来越多的能量逐渐由I x分量转移到I y分量,呈现单调递增的趋势。正是由于椭圆偏振光分量间的相互作用,导致了明模式E x分量和暗模式E y分量在超材料表面形成相消干涉,从而形成了电磁致诱导透明的现象。

对于图8.20(c)的情况,当未施加电压时,初始谐振状态与图8.20(a)的情况相同。但是在施加沿x轴方向的电压后,随着电场强度的增加,相移Δδ仅发生很小的变化。由式(8.11)可知,没有能量转移到I y分量。当电场强度足够大时,液晶分子形成沿x轴的均一排列,液晶层将不具有旋光效应,偏振旋转角β等于0。最终,在整个施加电场的过程中,在光强度I x和I y分量之间没有发生能量转移。所以,在这种情况下,仅仅是电偶极谐振位置随着液晶分子折射率的变化向低频移动,而没有产生电磁致诱导透明现象。