磁流体填充THz光子晶体的实验和分析

系统的磁光效应可以通过人工电磁谐振得到显著增强,若将磁流体填充到光子晶体中,利用光子晶体的导模谐振效应增强这一磁光微结构器件在THz波段的磁光效应,有望获得高灵敏度的磁场传感,下面通过实验和理论加以证实。

1.无外磁场时的结果

实验装置如图7.20所示,磁流体被0.5 mm厚的石英玻璃片封装于硅光子晶体芯片PC1和PC2中,磁场依然采用Voigt配置,即磁场方向垂直于THz波的传播方向和偏振方向。未施加磁场时填充四种不同浓度的磁流体的实验结果,如图7.21所示。对于PC1,未填充磁流体时的光子晶体导模谐振位置在0.87 THz,填充磁流体后谐振频率明显地向高频移动,并随着磁流体浓度的增加,谐振谷进一步蓝移,且谐振谷的透过率下降,浓度为7.9%的磁流体的导模谐振位置在1.02 THz,而浓度为17.7%的磁流体的导模谐振位置移动到1.1 THz。PC2呈现出与PC1完全一致的实验结果,谐振谷从1.42 THz移动到1.7 THz。还要注意到,随着填充液体折射率的增大,谱线线型逐渐由对称变为不对称。这是由于填充液体后,光子晶体周期性平面的界面间将存在明显的F P效应,在6.1.1小节中分析过F-P效应的存在将引入非对称因子,使得谐振遵循式(6.5)描述的Fano模型。由于折射率越大,界面的相位失配和F-P效应越强,谱线的不对称性就越显著。

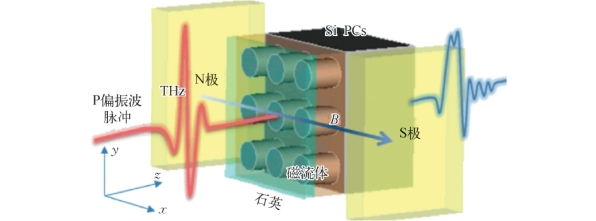
图7.20　磁流体填充光子晶体的实验装置图[12]

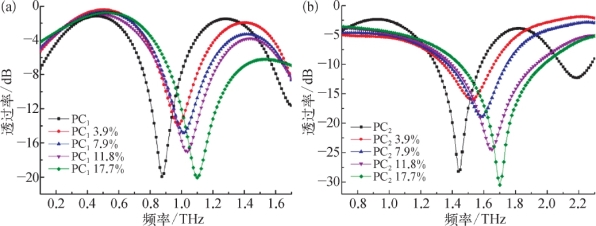
图7.21　不同浓度磁流体在未磁化状态下填充光子晶体的实验透射光谱[13]

(a)PC1;(b)PC2_

由于未施加磁场,磁流体并不具有THz磁光响应,填充不同浓度磁流体所带来的导模谐振蓝移一定是由磁流体的折射率不同造成的。通过对硅光子晶体进行建模,将光子晶体柱间隔空间的介质设定为这几种磁流体所对应的折射率和吸收系数,由FDTD算法计算模型的透过率,结果如图7.22所示。从图中可以发现,对于PC1和PC2,各折射率下的模拟谱线与各浓度磁流体的实验谱线吻合得非常好。通过将磁流体微量地填充到THz光子晶体中,测量光子晶体导模谐振谷的平移量,就可以得到磁流体中纳米颗粒浓度的定量信息,进而分辨磁流体的型号和种类。这种传感检测方式无须将大量磁流体样品填充进比色皿中进行测量,再计算材料的折射率和吸收谱线来进行判断,提高了传感灵敏度和可靠性,证明了THz光子晶体在微流体传感中的重要应用。

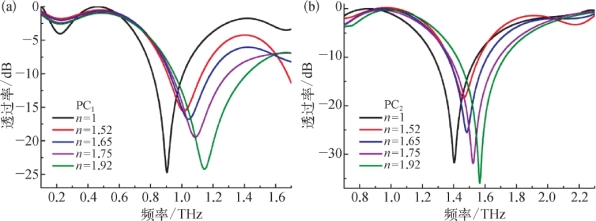
图7.22　不同折射率磁流体填充光子晶体的模拟透射光谱线[13]

(a)PC1;(b)PC2

2.有外磁场时的结果

由于在外磁场下的磁流体在THz波段具有磁光效应,因此磁流体填充的THz硅光子晶体就成为磁光-介质混合型的光子晶体(Ferrofluid Filled Photonic Crystal,FFPC)。按如图7.20所示施加由弱到强的外磁场进行THz-TDS实验,测得的填充浓度为7.9%的磁流体的FFPC的透射光谱线如图7.23(a)所示。已知磁流体的折射率会随磁场增大而减小,但图7.23(a)所示的光子晶体导模谐振谷在外磁场增大过程中并非简单地向低频移动,而是先分裂为两个谐振谷,然后随磁场增大分别向低频和高频方向移动,谐振强度也逐渐增强,1.02 THz频率处的原谐振谷的透过率逐渐增大,由谷变为峰。在150 m T下,低频谐振约移动到0.9 THz,高频谐振移动到1.14 THz,原谐振频率处透过率由-35 dB上升到-10 dB。因此,FFPC在外磁场下发生了磁致谐振分裂和诱导透明现象,在1 THz附近实现了外磁场调控的THz波强度调制,强度调制深度为25 dB,而谐振频率移动超过100 GHz。

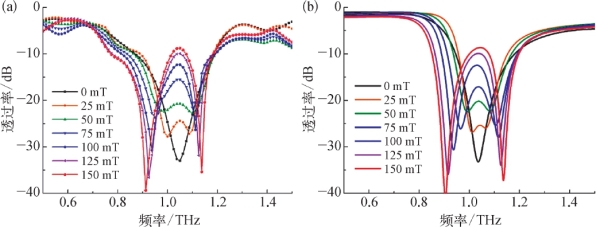
图7.23　在不同外磁场下,磁流体填充光子晶体的透射光谱线[12](www.xing528.com)

(a)实验;(b)理论计算

无论是在光学波段还是在THz波段,无论是铁氧体、InSb还是石墨烯,大量磁光器件中存在着磁光模式分裂现象,并且这一效应支撑着该类磁光器件的核心功能,如单向传输、磁光增强或诱导透明等。人工电磁诱导透明效应因其模拟了量子系统的行为而具有重要的物理意义,近年来受到广泛关注。而磁致相干诱导透明作为实现电磁诱导透明的一种重要方式,通过实验加以证实的报道仅有少数几例。上述研究工作的价值在于通过磁流体填充光子晶体在THz波段观察到了这一重要的物理现象。

磁流体在外磁场下的折射率变化是由横向磁光效应引起的,并且磁流体需要遵循式(7.6)所示的非互易张量及其张量元形式。在Voigt配置中,p偏振波在磁光介质中的电场矢量是椭圆偏振,但是在均匀统一的磁光介质中传输过程电位移矢量是线偏振的,且保持该偏振态不变,因此左、右旋光不存在有效折射率差异,也就不会发生磁光分裂。但是当磁光系统不再是均匀的,而是磁光-介质混合微结构时,如在FFPC中,p偏振波在磁流体中的电场矢量是椭圆偏振,在硅柱中时却为线偏振,这种偏振态的相位失配会导致左旋和右旋模式的有效折射率不再相等,从而发生磁光分裂。因此在Voigt配置下,只有磁光-介质混合型的人工磁光微结构材料才具有磁光分裂效应。

下面采用FEM方法数值求解FFPC的周期性单元在1 THz下的本征模式及其模场分布。模拟所需的材料的电磁参数采用7.3.2节中根据实验数据拟合出的数据,其中ε∞=2.9、ωp=3.4×1012 rad/s、γ=6.2×1012 rad/s和ωc=1.25×1013×B rad/(s·T),代入式(7.7)和式(7.8)得到在1 THz处磁流体的εxx=2.85和εxy=0.4i,硅的介电常数为εSi=11.7;在x和y方向各设置一对周期性边界条件。模拟结果证实了器件中的本征模式正是左旋(CCW)和右旋(CW)磁光模式,如图7.24(a)所示。这两个模式分别绕着磁流体与硅光子晶体柱的界面沿逆时针和顺时针方向在x-y平面内进行旋转,在垂直于周期平面的z方向没有振动分量。同时证实了,这两个模式在外磁场下有着不同的有效折射率n-和n+,无磁场时n+=n-,施加外磁场后两者开始分裂,左旋模式的有效折射率n+随着磁场增大而增大,右旋模式的有效折射率n-则随着磁场增大而减小,当外磁场达150 m T时,两者间的有效折射率差Δn达到0.023。这样单个光子晶体导模谐振就变为两个磁光导模谐振,而磁光旋转模式有效折射率的变化会引起对应磁光导模谐振频率的移动,满足

式中,ω0=2π×1.02×1012 rad/s为无外磁场时的原始导模谐振频率;磁流体回旋频率ωc=1.25×1013×B rad/(s·T)正比于外磁场。因此ω±是外磁场的函数,这里的下标“+”为左旋磁光导模谐振,W+随外磁场增加向高频移动,“-”为右旋磁光导模谐振,W-随外磁场增加向低频移动。如图7.24(b)所示,根据式(7.23)计算的谐振频率随外磁场变化的曲线与实验数据吻合得很好。

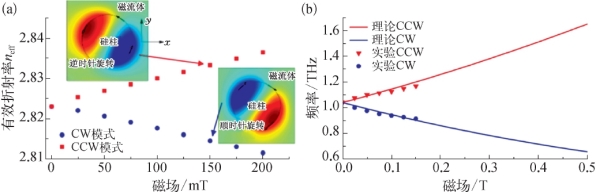
图7.24　

(a)磁流体填充光子晶体的左旋和右旋磁等离子体模式的有效折射率随外磁场的变化(数值模拟结果),插图为左、右旋模式的模场分布与旋向;(b)磁等离子体导模谐振的中心频率随外磁场的变化(实验与理论计算结果)[12]

既然光子晶体在填充磁流体后的导模谐振谱线遵从Fano线型,在FFPC中,磁光导模谐振的电场的复振幅谱可以用Fano模型来描述：

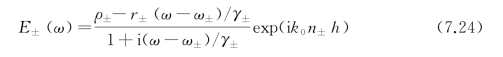
式中,ρ±=(n±-1)/(n±+1)为振幅透射比;r±=1-ρ±为振幅反射比;γ±为谐振线宽;n±为模式的有效折射率;k 0为真空中的波矢量;h为模型厚度。两个磁光模式的叠加将形成干涉效应,其强度谱可写为

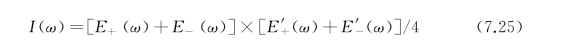
式中,E'±(ω)为E±(ω)的复共轭。将不同外磁场下模拟计算得到的n±和ω±以及实验测得的γ±参数代入式(7.24)和式(7.25)计算,可以得到Fano模型下器件的透射光谱线,如图7.23(b)所示,可见理论计算得到的谱线与图7.23(a)所示的实验谱线非常一致。因此,FFPC在外磁场下的THz波诱导透明效应是由分裂的两个磁光旋转模式的相干叠加产生的。

利用上述效应中谐振峰的移动进行的磁场传感具有高达1 mT/GHz的灵敏度,这是因为在磁光分裂和相干诱导透明过程中,增强了磁流体与THz波的相互作用,同时产生了磁光增强效应,提高了器件的灵敏度。

本节在实验上系统地研究了不同浓度的有机载液磁流体在THz波段的光学性质和横向磁光效应,发现了磁流体在THz波段的折射率和吸收系数随着磁纳米颗粒浓度变化的关系。在实验上发现并从理论上证实了THz磁流体填充的磁-硅光子晶体在THz波段的磁致导模谐振分裂和相干诱导透明效应,为THz波的磁场调控和利用THz技术进行微弱磁场传感奠定了基础。磁诱导透明频段范围内器件可实现调制深度为25 dB的强度调制,利用此效应中谐振峰的移动特性进行的磁场传感的灵敏度可高达1 m T/GHz。