磁流体的磁光特性简介

本小节介绍磁流体在外磁场横向配置下的磁光特性,即横向磁光效应。在逐渐增加外磁场强度时,我们测量了浓度为7.9%的磁流体的THz时域信号,如图7.16(a)所示。从图中可以发现在不同强度的磁场下,太赫兹脉冲延迟时间不一样,这说明磁流体的折射率发生了变化。图7.16(b)显示了在1 THz处折射率随着外磁场强度增加的变化趋势,从图中可以看到一个有趣的现象：折射率随着外磁场强度增加的变化过程分为两个阶段,第一个阶段在外磁场强度从0增加到10 m T时,太赫兹脉冲延迟时间逐渐变大,其对应的磁流体在1 THz处的折射率从1.652增加到1.668;第二个阶段是当外磁场强度超过10 m T后,太赫兹脉冲延迟时间开始减小,对应的磁流体在1 THz处的折射率从在10 mT时的1.668逐渐降低到150 m T时的1.656。

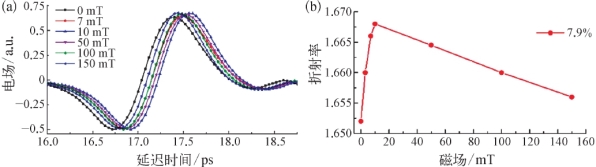
图7.16　

(a)不同外磁场强度下,7.9%的磁流体的太赫兹时域信号;(b)不同外磁场强度时,7.9%的磁流体在1 THz处的折射率变化[9]

此外,在实验中发现了另一个有意思的现象：当撤去外磁场后,太赫兹脉冲没有返回到初始位置,只是瞬间转回到延迟时间最大的位置。此时如果再次施加外磁场,并将外磁场强度从0逐渐增加到150 m T,在1 THz处的折射率从1.668再次下降到1.656,这一过程与之前提到的第二阶段的变化规律完全相同,而没有出现第一阶段的变化规律(从1.652到1.668的增加过程)。另外,第二阶段的折射率随外磁场强度增加/取消的变化是瞬时的,而第一阶段的变化需要一定的响应时间,这说明这两个阶段的折射率变化的物理过程是不同的。根据以上分析,定义第一个阶段为“结构变化诱导折射率变化的过程”,这个过程与弱磁场下磁流体的磁化过程密切相关;定义第二个阶段为“Voigt磁光效应诱导双折射的过程”,这个过程源于磁流体在达到饱和磁化(即形成稳定磁链)后,受横向磁场调控的磁等离子体效应。在下面两节的讨论中,我们将根据实验数据具体分析这两个阶段磁流体折射率的变化情况。

1.结构变化引起的折射率变化

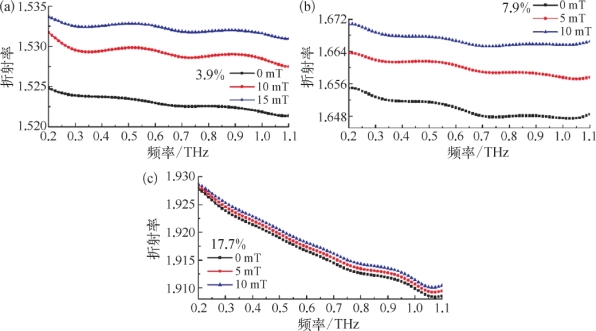
图7.17　3.9%、7.9%和17.7%的磁流体在弱磁场下的折射率变化[9]

(a)3.9%;(b)7.9%;(c)17.7%

这里研究第一阶段的磁流体折射率随外磁场的变化规律。图7.17显示了浓度为3.9%、7.9%和17.7%的磁流体在不同强度外磁场下的折射率变化。这三种磁流体的最大折射率差分别为0.012、0.016和0.002,尽管三个样本具有不同的折射率和色散,但其随外磁场强度变化的趋势是一致的。在外磁场的作用下,被磁化的磁纳米颗粒开始团簇形成磁粉团,当这个磁粉团的磁场力与范德瓦耳斯力、载液张力等达到平衡时,达到饱和稳定状态,此时磁纳米颗粒形成沿着磁场方向的有序链。在磁链形成过程中磁流体在微观结构上的变化诱导了折射率的变化,一旦磁链饱和磁化后,这些磁链趋于稳定,结构不再变化,因此不再对折射率变化有贡献。如果去掉外磁场,在不对磁流体进行如超声振动、加热等去磁处理的情况下,这个磁化状态可以保持较长的一段时间。

基于以上分析,利用Bruggman有效介质理论来拟合这种结构变化诱导的折射率变化。由于磁流体的折射率是矿物油和纳米颗粒的综合作用,磁流体的初始状态和最终状态分别为单分散状态下含纳米颗粒的矿物油和具有磁链排布的磁纳米颗粒的矿物油。以这两种介质的混合状态作为中间态,在不同外磁场作用下,磁流体中磁链状态的体积分数f决定了磁流体折射率的变化。因此,在磁链形成过程中的磁流体的折射率可以表示为式(7.21)[10]：

(www.xing528.com)

式中,ε1是没有磁化时分散状态的介电常数;ε2是饱和磁化后的介电常数;f是铁磁流体中磁链状态的体积分数,与磁化率成正比,并且可以用Langevian方程来描述[11]：

式中,M为施加特定电磁场后的磁化率;M s分别为浓度为3.9%、7.9%和17.7%的磁流体的饱和磁化率,分别设定为20 mT、40 mT和90 mT;k是与温度和纳米颗粒浓度相关的系数;H是外磁场的强度。图7.18所示的初始状态和最终状态的实验数据可以分别取为ε1和ε2。在温度一定的情况下,随着纳米颗粒浓度的增加,k减小,因此分别选择三种不同浓度磁流体的拟合系数k为0.94、0.76和0.55。根据式(7.21)和式(7.22),拟合1 THz处三个样品的折射率变化,如图7.18所示。从图中可以看出,三条理论曲线都与各自的实验数据吻合得很好,这说明把等效介质理论与Langevian磁化模型相结合确实可以很好地描述磁流体结构变化引起的折射率变化。

图7.18　当外磁场强度变化时,3.9%、7.9%和17.7%的磁流体折射率变化测量值(红点)和理论拟合值(黑线)[9]

(a)3.9%;(b)7.9%;(c)17.7%

2.横向磁光效应引起的双折射

下面讨论折射率变化的第二阶段。当外磁场的强度继续增加时,磁流体中的磁链簇结构在显微镜下保持稳定,因此,磁流体的折射率变化不再受磁流体内部结构变化的影响。正因为这些有序的磁链簇结构的存在,使得磁流体在宏观上表现出磁性,因此可以用磁等离子体模型来描述其磁光性质。磁流体的磁光特性来源于这些磁粉团的自旋磁矩,在外磁场作用下自旋磁矩的定向排列使得磁流体具有铁磁材料的磁光特性,如法拉第效应和Voigt横向磁光效应。

实验中磁场在系统里的摆放为Voigt横向磁光配置,如图7.15(a)所示。根据理论分析,在这种磁场配置下,只有p偏振THz波会受到外磁场的影响,而s偏振光与外磁场没有关系。如图7.19所示,当外磁场强度从10 m T增加到150 m T时,p偏振方向的太赫兹波入射样品,浓度为3.9%、7.9%和17.7%的磁流体在1 THz处的折射率n p分别下降了0.009、0.013和0.008。而当太赫兹辐射源的偏振方向偏转90°(即入射光为s偏振方向)时,折射率并没有改变。因此,双折射现象出现与否完全依赖于电磁场的偏振态,这一特性与磁光材料的Voigt磁光效应相同。

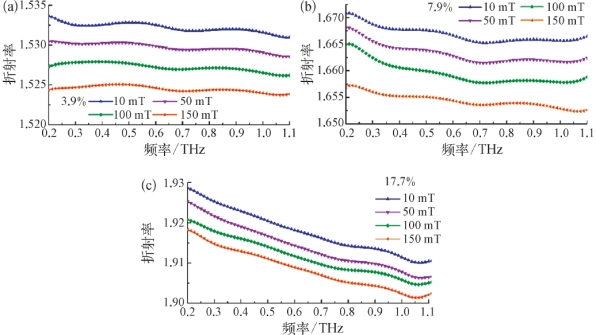
图7.19　在不同外磁场作用下,3.9%、7.9%和17.7%的磁流体的折射率(实验结果)[9]

(a)3.9%;(b)7.9%;(c)17.7%