单轴机械可调谐太赫兹超材料优化方案

本小节介绍一种由PDMS弹性基底和“I”形谐振单元结构构成的太赫兹超材料,通过施加拉力使之产生机械拉伸形变,实现了机械调谐功能。

为了简化谐振单元结构,减小金属谐振单元本身在受力形变下的结构形变,突出基底形变,增强谐振频率平移响应的敏感度,选择了“I”形结构作为基本谐振单元,如图6.25(a)所示。金属层厚度为100 nm,基底厚度为100μm。详细结构尺寸参数如下：a=63μm,s=48μm,l=60μm,w=5μm。当太赫兹波偏振方向以图中E方向正入射到超材料表面时,整个谐振单元可以视为偶极振荡。在入射电场的作用下,大量的表面感应电荷聚集于“I”形结构的上下边缘。这些感应电荷在上下两个相邻“I”形谐振结构之间的区域形成不断变换的电势差,类似于平行平板电容间的交变电场,使上下相邻谐振单元之间形成强烈的振荡电场耦合。谐振频率处的瞬时电场分布如图6.25(b)所示,从图中可以看到在振荡过程中,几乎所有的能量都被集中于相邻谐振单元之间的狭缝区域,所以狭缝宽度的微小变化都会强烈地影响超材料的谐振特性,从而改变其谐振频率。由基础电子电路原理可知,振荡频率f 0可以由等效电容C和等效电感L决定,其可以表示为

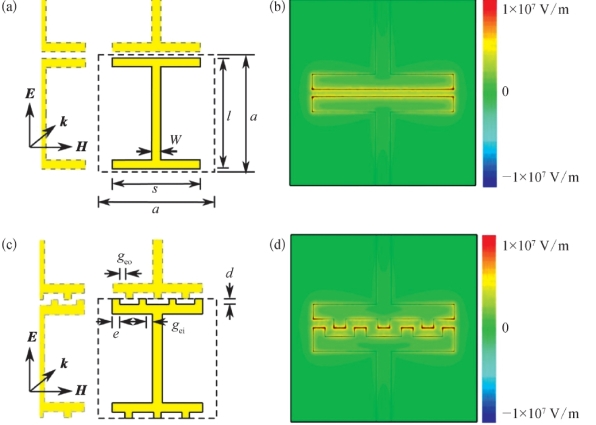
图6.25　单轴机械可调谐太赫兹超材料的结构示意图和谐振频率处的电场分布[14]

在平行平板电容的理论模型中,电容可以表示为

式中,ε为介质的电容率;S为平行平板面积;d为平行平板间的距离。考虑到样品金属层的厚度要远远小于构成谐振狭缝区域的金属边缘的长度和狭缝宽度,理论上狭缝区域的电场强度可以用有限长度平行金属线模型代替平行平板模型来描述,这样,狭缝区域的电容就可以进一步近似地表示为

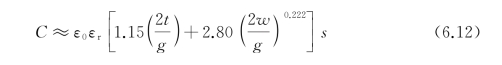
式中,ε0为自由空间的介电常数;εr为基底材料的相对介电常数;t为金属层的厚度;w为金属结构线宽;g=a-1为狭缝宽度;s为狭缝区域的长度。在太赫兹波垂直入射条件下,如果对样品施加一个沿振荡电场方向的外力,样品将会产生形变。由于“I”形结构单元与单元之间并不相连,在外力形变过程中,金属谐振结构本身会产生微小的形变。由于高弹性PDMS基底材料良好的机械延展性,外力产生的形变将主要集中于相邻单元结构之间的狭缝区域,所以随着外力作用导致形变加剧,狭缝的宽度g随之改变,宏观上超材料的谐振频率得到了有效调制。

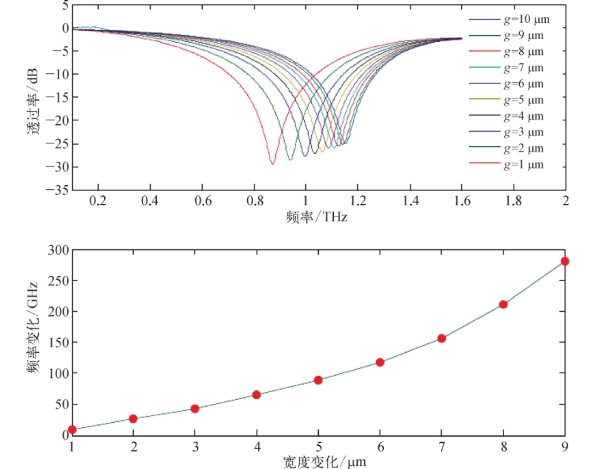
利用CST Microwave Studio模拟了“I”形单元结构间狭缝宽度对谐振频率的影响,模拟结果如图6.26所示。在模拟中,金属材料为金,参数设置如下：高频介电常数ε∞=1,等离子体频率ωP=1.37×1016 rad/s,碰撞频率γ=6.45×1012 Hz。依据太赫兹时域光谱系统的测量结果,PDMS基底材料的参数设置为相对介电常数εr=2.55,电导率σ=2.5×10-14 S/m。从模拟结果可以得到,假设初始狭缝宽度为g=10μm,当狭缝宽度从10μm减小到1μm时,超材料的谐振频率向低频移动,即谐振频率发生红移,由1.17 THz平移到0.86 THz,谐振频率的平移速度也由11.6 GHz/μm增加到304.5 GHz/μm。

(www.xing528.com)

图6.26　“I”形超材料谐振频率随狭缝宽度变化的模拟结果

为了进一步增强振荡,提高谐振的品质因数和超材料用于应力传感时的灵敏度,采用交叉指狭缝结构来代替上面结构模型中的平行直线狭缝。交叉指模型主要用于微波电路中集成电子元件设计,也被用于短线段耦合的可调谐开口谐振环结构和复合左右手传输线结构中,以获得更强的电容狭缝内电场。如图6.27所示,交叉指电容C IDC分别由交叉指部分的长度l IDC、交叉指数目N、交叉指线宽w、狭缝宽度g及基底材料有效介电常数εre决定,其可以表示为

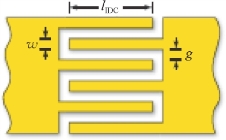
图6.27　交叉指模型示意图

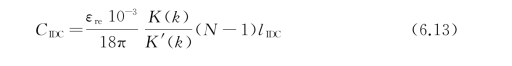
式中,第一类完全椭圆积分K(k)和其补集K'(k)的比值系数约为

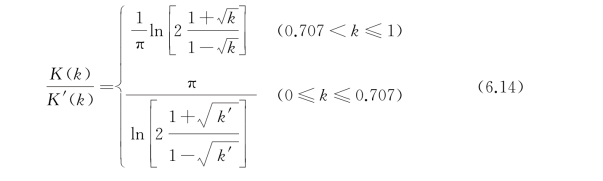
式中,平行电容相当于N=2的情况,所以平行电容C 0可表示为

式中,l 0为平行电容平行线长度。所以,交叉指电容又可以表示为

交叉指狭缝“I”形振荡单元结构如图6.25(c)所示。交叉指狭缝结构参数为d=3μm,e=4μm,g eo=3μm,g ei=4μm,谐振单元其他部分结构参数与平行直线狭缝模型相同。图6.25(d)为该谐振单元在谐振频率处的电场分布。在狭缝宽度不变的情况下,交叉指结构相当于更长的平行直线狭缝,与之前的平行直线狭缝结构相比,大大地增强了结构的等效电容,使电磁振荡能量更多地集中于狭缝区域。这将使超材料谐振谱线更加尖锐,从而提高谐振的品质因数,使得由相同狭缝宽度改变量引起的谐振频率平移加大,可调谐带宽加宽,获得更高的响应敏感度。